\(\left(-\dfrac{3}{5}\right)^2.\dfrac{5}{11}+\dfrac{9}{25}.\left(-\dfrac{16}{11}\right)\)

\(=\dfrac{9}{25}.\dfrac{5}{11}+\dfrac{9}{25}.\left(-\dfrac{16}{11}\right)\)

\(=\dfrac{9}{25}.\left[\dfrac{5}{11}+\left(-\dfrac{16}{11}\right)\right]\)

\(=\dfrac{9}{25}.\left(-1\right)\)

\(=-\dfrac{9}{25}\)

7\(x\).2 hay 7\(x^2\) vậy em?

7x^2 ạ

`a` là số tự nhiên không chia hết cho `3` nên a có dạng: 

`a = 3k + 1` hoặc `a = 3k + 2`

(`k` thuộc `N`*)

Mà a là số tự nhiên lẻ `=> a^2` là số tự nhiên lẻ `=> a^2 - 1` là số chẵn 

`=> a^2 ⋮ 2`

Để `a^2 - 1 ⋮ 6` thì  `a^2 - 1 ⋮ 3` (Vì `UCLN(2;3) = 1`)

- Xét `a = 3k + 1`

`=> a^2 -1 = (3k+1)^2 -1= 9k^2 + 6k + 1 - 1= 9k^2 + 6k^2 ⋮ 3` (Thỏa mãn)

- Xét `a = 3k + 2`

`=> a^2 -1 = (3k+2)^2 -1 = 9k^2 + 12k + 4 - 1= 9k^2 + 12k^2 + 3 ⋮ 3` (Thỏa mãn)

Vậy ...

\(\left(x+5\right)^2-4x^2\\=\left(x+5\right)^2-\left(2x\right)^2\\ =\left[\left(x+5\right)-2x\right]\left[\left(x+5\right)+2x\right]\\ =\left(x+5-2x\right)\left(x+5+2x\right)\\ =\left(-x+5\right)\left(3x+5\right)\)

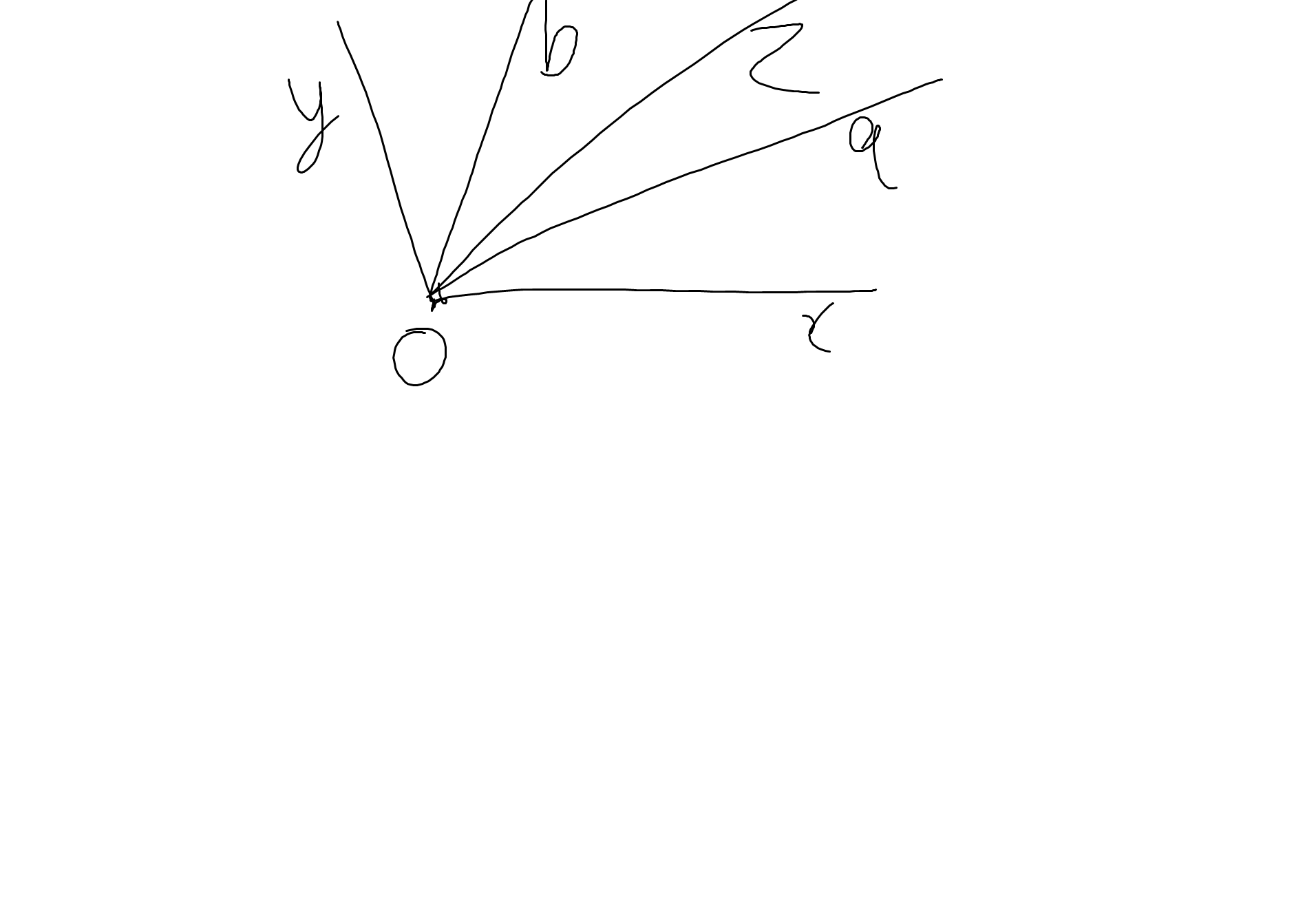
Oa là phân giác của góc xOz

=>\(\widehat{zOa}=\dfrac{\widehat{xOz}}{2}\)

Ob là phân giác của góc zOy

=>\(\widehat{zOb}=\dfrac{\widehat{zOy}}{2}\)

\(\widehat{aOb}=\widehat{zOa}+\widehat{zOb}=\dfrac{1}{2}\left(\widehat{xOz}+\widehat{zOy}\right)\)

\(=\dfrac{1}{2}\cdot\widehat{xOy}=\dfrac{1}{2}\cdot150^0=75^0\)

Kẻ tia `Ot` là tia đối của tia `Ox`

=> \(\widehat{xOt}=180^o\)

Ta có: 

\(\widehat{yOt}=\widehat{xOt}-\widehat{xOy}=180^o-120^o=60^o\)

=> \(\widehat{tOz}=\widehat{zOy}-\widehat{yOt}=134^o-60^o=74^o\)

Mà \(\widehat{xOz};\widehat{zOt}\) là 2 góc kề bù

=> \(\widehat{zOx}+\widehat{zOt}=\widehat{xOt}\)

=> \(\widehat{xOz}=\widehat{xOt}-\widehat{tOz}=180^o-74^o=106^o\)

Vậy ...

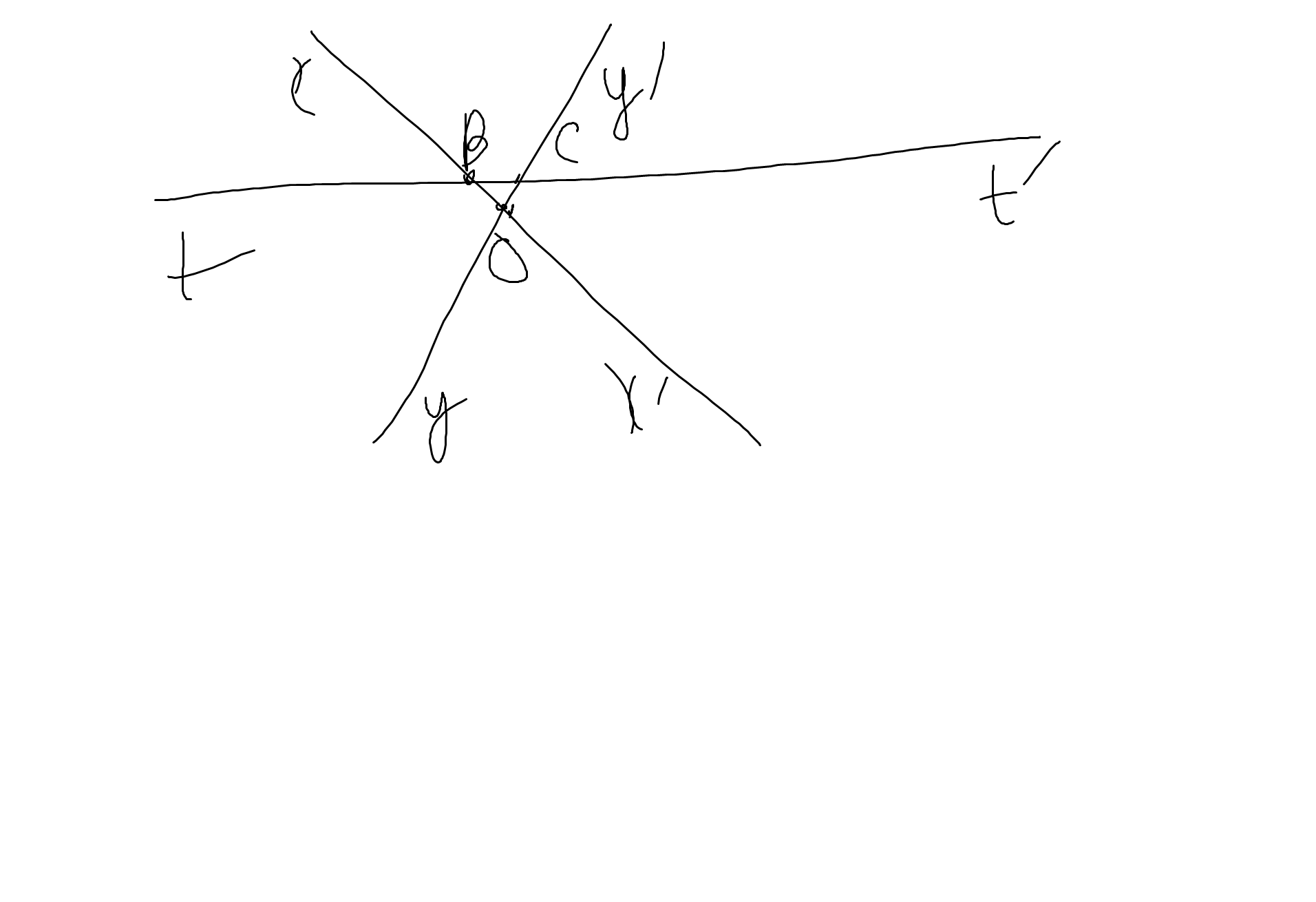
Bài 3: Các cặp góc so le trong là: \(\widehat{tBO};\widehat{BOC}\); \(\widehat{OBC};\widehat{yOB}\); \(\widehat{BCO};\widehat{x'OC}\); \(\widehat{t'CO};\widehat{BOC}\)

Các cặp góc đồng vị là:

\(\widehat{xBt};\widehat{xOy}\); \(\widehat{tBO};\widehat{x'Oy}\); \(\widehat{y'Ct'};\widehat{x'Oy'}\); \(\widehat{t'CO};\widehat{x'Oy}\)

Bài 2: 

Các cặp góc so le trong là \(\widehat{FEC};\widehat{ACB}\)

Các cặp góc đồng vị là \(\widehat{ADE};\widehat{ABC}\); \(\widehat{AED};\widehat{ACB}\)

Các cặp góc trong cùng phía là: \(\widehat{BDE};\widehat{B}\); \(\widehat{DEC};\widehat{ECB}\)

\(x^3+ax+b\\ =\left(x^3+4x^2+3x\right)+\left(-4x^2-16x-12\right)+\left(a+13\right)x+\left(b+12\right)\\ =x\left(x^2+4x+3\right)-4\left(x^2+4x+3\right)+\left(a+13\right)x+\left(b+12\right)\\ =\left(x-4\right)\left(x^2+4x+3\right)+\left(a+13\right)x+\left(b+12\right)\)

Để `x^3+ax+b` chia hết cho `x^2+4x+3` thì:

\(\left\{{}\begin{matrix}a+13=0\\b+12=0\end{matrix}\right.=>\left\{{}\begin{matrix}a=-13\\b=-12\end{matrix}\right.\)

Ta có: 

\(1+2+3+...+n\)

Số lượng số hạng là: `(n-1):1+1=n` (số hạng) 

Tổng của dãy số là: `(n+1)*n/2` 

Áp dụng ta có:

\(\dfrac{1}{1+2+3}+\dfrac{1}{1+2+3+4}+....+\dfrac{1}{1+2+3+...+100}\\ =\dfrac{1}{\dfrac{3\cdot\left(3+1\right)}{2}}+\dfrac{1}{\dfrac{4\cdot\left(4+1\right)}{2}}+...+\dfrac{1}{\dfrac{100\cdot\left(100+1\right)}{2}}\\ =\dfrac{2}{3\cdot4}+\dfrac{2}{4\cdot5}+...+\dfrac{2}{100\cdot101}\\ =2\left(\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+...+\dfrac{1}{100\cdot101}\right)\\ =2\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{100}-\dfrac{1}{101}\right)\\ =2\left(\dfrac{1}{3}-\dfrac{1}{101}\right)\\ =2\cdot\dfrac{98}{303}\\ =\dfrac{196}{303}\)

trả lời xong nhớ cho coin

ko bế ơi

like thôi