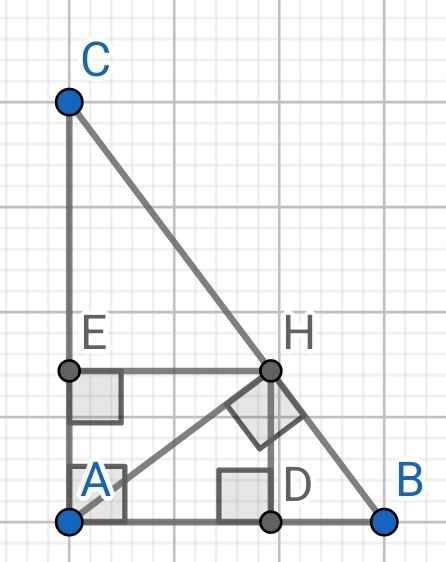
Cho tam giác ABC vuông tại A có AB <AC, đường cao AH, H thuộc BC. a) Chứng minh rằng tam giác ABC đồng dạng tam giác HAC, từ đó suy ra AC^2= HC. BC. b) Cho BH =1 cm; HC =4 cm . Tính độ dài các cạnh AC và AH c) Kẻ BE là đường phân giác trong của tam giác ABC, E thuộc AC. Đường thẳng qua C vuông góc với BE tại D và cắt A B tại I . Chứng minh: IA.IB=2AD.ID-AI^2.
Xin trợ giúp câu c.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét hai tam giác vuông: ∆BDH và ∆BHA có:
∠B chung
⇒ ∆BDH ∽ ∆BHA (g-g)
b) Xét hai tam giác vuông: ∆AHB và ∆ADH có:
∠A chung
⇒ ∆AHB ∽ ∆ADH (g-g)
⇒ AH/AD = AB/AH
⇒ AH² = AD.AB

a) x = 2 A = (2 - 6)/(2 + 2) = -1
b) B = 6/(x - 2) + x/(x + 2) - 8/(x² - 4)
= [6(x + 2) + x(x - 2) - 8]/[(x - 2)(x + 2)]
= (6x + 12 + x² - 2x - 8)/[(x - 2)(x + 2)]
= (x² + 4x + 4)/[(x - 2)(x + 2)]
= (x + 2)²/[(x - 2)(x + 2)]
= (x + 2)/(x - 2)
c) P = A.B
= (x - 6)/(x + 2) . (x + 2)/(x - 2)
= (x - 6)/(x - 2)
Để P = 2/3 thì
(x - 6)/(x - 2) = 2/3
3(x - 6) = 2(x - 2)
3x - 18 = 2x - 4
3x - 2x = -4 + 18
x = 14
Vậy x = 14 thì P = 2/3

tại x = 1 , y = -3
x^2 - 4y^2/x -2y = 1^2 - 4.(-3)^2/1 -2.(-3) = 2 - 36 + 6 = -28
Đặt \(A=\dfrac{x^2-4y^2}{x-2y}\)
=>\(A=\dfrac{\left(x-2y\right)\left(x+2y\right)}{x-2y}=x+2y\)
Thay x=1 và y=-3 vào A, ta được:
\(A=1+2\cdot\left(-3\right)=1-6=-5\)

Thay x=1 và y=-3 vào phân thức \(\dfrac{x^2-y^2}{x-2y}\), ta được:
\(\dfrac{1^2-\left(-3\right)^2}{1-2\cdot\left(-3\right)}=\dfrac{1-9}{1+2\cdot3}=\dfrac{-8}{7}\)

ĐKXĐ: \(4x^2-1\ne0\)
=>\(x^2\ne\dfrac{1}{4}\)
=>\(x\notin\left\{\dfrac{1}{2};-\dfrac{1}{2}\right\}\)

a: Để (d) song song với đường thẳng y=-x+m thì
\(\left\{{}\begin{matrix}m-1=-1\\m\ne4\end{matrix}\right.\)
=>m=0
b: Thay x=1 và y=5 vào y=2x+b, ta được:
\(b+2\cdot1=5\)
=>b+2=5
=>b=3

Bài 1:
Gọi A là biến cố "Số xuất hiện trên quả bóng là số nguyên tố"
=>A={2;3;5;7;11}
=>n(A)=5
\(n\left(\Omega\right)=12-1+1=12\)
\(\Leftrightarrow P_A=\dfrac{5}{12}\)

\(4h25p=\dfrac{53}{12}\left(giờ\right)\)
Độ dài quãng đường từ nhà đến tỉnh là:
\(\dfrac{53}{12}\cdot14=\dfrac{371}{6}\left(km\right)\)

a:
Sửa đề: ΔABC~ΔCBD
BD=BA+AD=5+4=9(cm)
Xét ΔABC và ΔCBD có
\(\dfrac{AB}{CB}=\dfrac{BC}{BD}\left(\dfrac{4}{6}=\dfrac{6}{9}=\dfrac{2}{3}\right)\)
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔCBD
b: ΔABC~ΔCBD
=>\(\dfrac{AC}{CD}=\dfrac{BC}{BD}\)
=>\(\dfrac{5}{CD}=\dfrac{2}{3}\)
=>\(CD=5\cdot\dfrac{3}{2}=7,5\left(cm\right)\)