Em cần giúp câu c và d bài 4 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\left(1-\dfrac{1}{2}\right)xy^2-4xy=\dfrac{1}{2}xy^2-4xy\)

\(-5x^3y^2+10x^3y^2+\left(-\frac{3}{4}x^3y^2\right)-x^3y^2\)
\(=x^3y^2.\left(-5+10-\frac{3}{4}-1\right)\)
\(=\frac{13}{4}.x^3y^2\)
a, \(-6x^3y^2+\left(10-\dfrac{3}{4}\right)x^3y^2=-6x^3y^2+\dfrac{37}{4}x^3y^2\)

a. \(A=-5.\left(-1\right)^2-\frac{1}{3}.\left(-1\right)=-\frac{14}{3}\)
b. \(B=\frac{1}{2}\left(-2\right)^2-3\left(-\frac{1}{3}\right)^2=\frac{5}{3}\)
c. \(P=2.\left(-\frac{1}{2}\right)^3+3\left(-\frac{1}{2}\right)^2.\frac{2}{3}+\left(\frac{2}{3}\right)^2=\frac{25}{36}\)
d. \(12ab^2=12.\left(-\frac{1}{3}\right).\left(-\frac{1}{6}\right)^2=-\frac{1}{9}\)

Đặt \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=t\Rightarrow\hept{\begin{cases}a=bt\\b=ct\\c=dt\end{cases}}\)
\(\left(\frac{a+b+c}{b+c+d}\right)^4=\left(\frac{bt+ct+dt}{b+c+d}\right)^4=t^4\)
\(\frac{ab}{cd}=\frac{bt.ct}{cd}=\frac{ct^2.dt^2}{cd}=t^4\)
Suy ra đpcm.

M = -2x3y. (-3x2y3)
= -2.(-3) .(x3x2).(yy3)
= 6x5y4
Bậc 9. Hệ số : 6
N= (-3x2y)2.(-5)xy3
= 9x4y2.(-5) xy3
= 9.(-5) x4xy2y3
= -45x5y5
Bậc 10. Hệ số -45
\(M=6x^5y^4\)
bậc 9 ; hệ số 6
\(N=\left(9x^4y^2\right)\left(-5xy^3\right)=-45x^5y^5\)
bậc 10 ; hệ số -45

ta có :
\(D=\frac{6-x+2}{x-6}=-1+\frac{2}{x-6}\)nhỏ nhất khi \(x-6=-1\Leftrightarrow x=5\)
khi đó D = -3

A= 3x2 - 2x + 3
= 3(x2- 2/3x + 1/9 ) + 8/3
= 3(x-1/3)2 + 8/3 > 8/3 \(\forall\)x
dấu ''='' xảy ra <=> x = 1/3
/HT\
Nhầm đề rồi mấy bạn trả lời
Bảo là giá trị nguyên của ,\(\frac{2x-3}{3x+2}\) , các bạn ghi là \(3x^2-2x+3\)rồi
HT

Áp dụng đlí Pytago với tam giác vuông ta được:
\(a^2+b^2=c^2\)
Trong đó: a,b lần lượt là 2 cạnh góc vuông
c là cạnh huyền
Áp dụng vào bài toán ta đc:
\(60^2+b^2=100^2\)
\(\Leftrightarrow b^2=100^2-60^2\)
\(\Leftrightarrow b^2=\left(100-60\right)\left(100+60\right)\)
\(\Leftrightarrow b^2=40\cdot160=6400\)
\(\Leftrightarrow b=80\)(vì b>0)
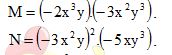
a, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=AB^2+AC^2=5cm\)
b, Xét tam giác ABD và tan giác EBD có
BD _ chung
^ABD = ^EBD
Vậy tam giác ABD = tam giác EBD (ch-gn)
c, AD = ED ( 2 cạnh tương ứng )
Xét tam giác IAD và tam giác CED có
^IDA = ^CDE ( đ . đ )
AD = ED ( cmt )
Vậy tam giác IAD = tam giác CED (ch-cgv)
=> ID = CD ( 2 cạnh tương ứng )
Xét tam giác IDC có
ID = DC => tam giác IDC cân tại D