(8x2+3)(8x2-3)-(8x2-1)2=22
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c. Ta có: x3 + 9x2 + 27x + 27
= x3 + 3.x2.3 + 3.x.32 + 33
= (x + 3)3
Thay x = 97, ta được: (x + 3)3 = (97 + 3)3 = 1003 = 1000000
nha bạn chúc bạn học tốt ạ
x3 + 9x2 + 27x + 27 = ( x + 3 )3
Thay x = 97 bthuc = ( 97 + 3 )3 = 1003 = 1000000

Dùng Định lý Thales có được không ạ?
+) ED//AC (gt)
=> Theo định lý Thales ta có \(\frac{AE}{AB}=\frac{CD}{BC}\)
+) FD//AB (gt)
=> Theo định lý Thales ta có \(\frac{AF}{AC}=\frac{BD}{BC}\)
\(\Rightarrow\frac{AE}{AB}+\frac{AF}{AC}=\frac{CD}{BC}+\frac{BD}{BC}=\frac{BC}{BC}=1\text{ (đpcm)}\)

Câu 1:
a. x2 – 2xy – 4z2 + y2 = (x2 – 2xy + y2) – 4z2
= (x – y)2 – (2z)2 = (x – y + 2z)(x – y – 2z)
Thay x = 6; y = -4; z= 45 vào biểu thức ta được:
[ 6- (- 4) + 2.45]. [6- (-4) – 2.45]
= (6 + 4 + 90)(6 + 4 – 90) = 100.(-80) = -8000
b. 3(x – 3)(x + 7) + (x – 4)2 + 48
= 3(x2 + 7x – 3x – 21) + x2 – 2.4x + 42 + 48
= 3(x2 + 4x – 21 ) + x2 – 8x + 16 + 48
Thay x = 0,5 vào biểu thức ta được:
(2.0,5 + 1)2 = (1 + 1)2 = 4
Câu 2:
a. x2 – x – y2 – y
= (x2 – y2) – (x + y)
= (x + y)(x – y) – (x + y)
= (x + y)(x – y – 1)
b. x2 – 2xy + y2 - z2
= (x2 – 2xy + y2) – z2
= (x – y)2 – z2
= (x – y + z)(x – y – z)

a. Ta có: x2y3.35xy = 35x3y4
5.7x3y4 = 35x3y4
Suy ra: x2y3.35xy = 5.7x3y4
Vậy 
b. Ta có: x2(x + 2)(x + 2) = x2(x + 2)2
x(x + 2)2.x = x2(x + 2)2
Suy ra: x2(x + 2)(x + 2) = x(x + 2)2.x
Vậy 
c) Ta có:
(3 – x). (9 - x2) = (3 – x).( 3 - x).(3 + x)= (3 – x)2(3 + x) (1)
Và ( 3 + x).( x2 – 6x + 9) = (3 + x).(x - 3)2 = (3 + x). (3 - x)2) (2)
( Vì (x - 3) = -(3 - x) nên (x - 3)2 = [- (3 - x)]2 = (3- x)2)
Từ (1) và (2) suy ra: (3 - x).(9 - x2) = (3 + x).(x2 – 6x + 9)
Do đó: 
d. Ta có: (x3 – 4x).5 = 5x3 – 20x
(10 – 5x)(- x2 – 2x) = - 10x2 – 20x + 5x3 + 10x2 = 5x3 – 20x
Suy ra: (x3 – 4x).5 = (10 – 5x)(- x2 – 2x)
Vậy: 

a) (x-1)(x+6)
b) (5x-1)(y+x)
c) -(6x^2-7cx+2)
Câu 1:
a. x4 + 2x3 + x2 = x2(x2 + 2x + 1) = x2(x + 1)2
b. x3 – x + 3x2y + 3xy2 + y3 – y
= (x3 + 3x2y + 3xy2 + y3) – (x + y) = (x + y)3 – (x + y)
= (x + y)[(x + y)2 – 1] = (x + y)(x + y + 1)(x + y - 1)
c. 5x2 – 10xy + 5y2 – 20z2 = 5(x2 – 2xy + y2 – 4z2)
= 5[(x2 – 2xy + y2) – 4z2] = 5[(x – y)2 – (2z)2]
= 5(x – y + 2z)(x – y – 2z)
Câu 2:
+) Ta có: a3 + b3 = (a + b)3 – 3ab(a + b)
Thật vậy, VP = (a+ b)3 – 3ab (a + b)
= a3 + 3a2b + 3ab2 + b3 – 3a2b – 3ab2
= a3 + b3 = VT
Nên a3 + b3 + c3 = (a + b)3 – 3ab(a + b) + c3(1)
Ta có: a + b + c = 0 ⇒ a + b = - c (2)
Thay (2) vào (1) ta có:
a3 + b3 + c3 = (-c)3 – 3ab(-c) + c3 = -c3 + 3abc + c3 = 3abc
Vế trái bằng vế phải nên đẳng thức được chứng minh.

vi x,y,z la so duong => 0<x<4,0<y<4,0<z<4.
lai co (x+y+z)/z > xy+1 => x+y>xyz.
>= chứ nhỉ
dự đoán dấu "=" xảy ra <=> x = y = 1 ; z = 2
bất đẳng thức cần chứng minh tương đương với \(\frac{x+y}{xyz}\ge1\)
Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\frac{x+y}{xyz}=\frac{x}{xyz}+\frac{y}{xyz}=\frac{1}{yz}+\frac{1}{xz}\ge\frac{4}{z\left(x+y\right)}\)
Áp dụng bất đẳng thức AM-GM ta có :
\(z\left(x+y\right)\le\frac{\left(z+x+y\right)^2}{4}=\frac{4^2}{4}=4\)
\(\Rightarrow\frac{x+y}{xyz}\ge\frac{4}{z\left(x+y\right)}\ge\frac{4}{4}=1\)
Vậy ta có đpcm . Dấu "=" xảy ra <=> \(\hept{\begin{cases}x,y,z>0\\z=x+y\\x+y+z=4\end{cases}}\Rightarrow\hept{\begin{cases}x=y=1\\z=2\end{cases}}\)

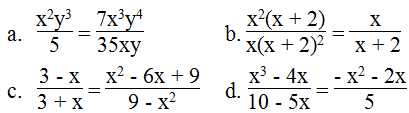
ta có :
\(\left(8x^2+3\right)\left(8x^2-3\right)-\left(8x^2-1\right)^2=22\)
\(\Leftrightarrow64x^4-9-\left(64x^4-16x^2+1\right)=22\Leftrightarrow16x^2=32\Leftrightarrow x^2=2\)
\(\Leftrightarrow x=\pm\sqrt{2}\)
\(\Leftrightarrow64x^4-9-64x^4+16x^2-1=22\Leftrightarrow16x^2=32\Rightarrow x^2=2\Rightarrow\orbr{\begin{cases}x=\sqrt{2}\\x=-\sqrt{2}\end{cases}}\)