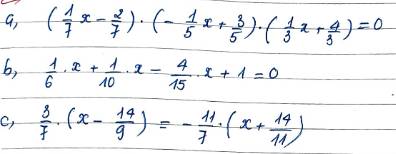Bài 8. Cho số nguyên tố p và bốn số nguyên dương a; b; c; d thỏa mãn
[a; a+ p^2] = [b; b+ p^2] = [c; c+ p^2] = [d; d + p^2]:
Chứng minh rằng trong bốn số a; b; c; d có ít nhất hai số bằng nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Muốn có coin bạn cần phải tham gia các hoạt động của Olm nhé!

Trả lời nhanh thì được 10 điểm!!!
Nhiều câu trả lời càng tốt, vì nó sẽ giúp tui bình luận nhiều hơn đấy!!! Trả lời đi!!!!!!!!!!!!!!!!!!!!!!!!!!!!


Giải:
Tổng số tiền mà lớp 4A thu được là:
20 000 x 38 = 760 000 (đồng)
Phân số chỉ số tiền còn lại của lớp 4A là:
1 - \(\dfrac{5}{8}\) = \(\dfrac{3}{8}\) (số tiền)
Số tiền còn lại của lớp 4A là:
760 000 x \(\dfrac{3}{8}\) = 285 000 (đồng)
Đáp số:...

a: \(\left(\dfrac{1}{7}x-\dfrac{2}{7}\right)\left(-\dfrac{1}{5}x+\dfrac{3}{5}\right)\left(\dfrac{1}{3}x+\dfrac{4}{3}\right)=0\)
=>\(\dfrac{1}{7}\left(x-2\right)\cdot\dfrac{-1}{5}\cdot\left(x-3\right)\cdot\dfrac{1}{3}\left(x+4\right)=0\)
=>(x-2)(x-3)(x+4)=0
=>\(\left[{}\begin{matrix}x-2=0\\x-3=0\\x+4=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=2\\x=3\\x=-4\end{matrix}\right.\)
b: \(\dfrac{1}{6}x+\dfrac{1}{10}x-\dfrac{4}{15}x+1=0\)
=>\(x\left(\dfrac{1}{6}+\dfrac{1}{10}-\dfrac{4}{15}\right)=1\)
=>\(x\cdot\dfrac{5+3-8}{30}=1\)
=>x*0=1(vô lý)
=>\(x\in\varnothing\)
c: \(\dfrac{3}{7}\left(x-\dfrac{14}{9}\right)=-\dfrac{11}{7}\left(x+\dfrac{14}{11}\right)\)
=>\(\dfrac{3}{7}x-\dfrac{42}{63}=-\dfrac{11}{7}x-\dfrac{14}{7}\)
=>\(2x=-\dfrac{14}{7}+\dfrac{42}{63}=-2+\dfrac{2}{3}=-\dfrac{4}{3}\)
=>\(x=-\dfrac{2}{3}\)

(108 - 54 x 2) x (2 + 4 + 6 + 8 + 10)
= (108 - 108) x (2 + 4 + 6 + 8 + 10)
= 0 x (2 + 4 + 6 + 8 + 10)
= 0