Giá nhập vào một bộ trò chơi là 100 nghìn đồng.Giá bán của nó là 150 nghìn đồng. Nếu cửa hàng muốn thu lợi nhuận ít nhất 5 thì họ cần giảm giá cho sản phẩm này tối đa bao nhiêu phần trăm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để thu lợi nhuận ít nhất \(5\%\)thì giá bán tối thiểu là: \(100.\left(1+5\%\right)=105\)(nghìn đồng)
Giá giảm tối đa số tiền là: \(150-105=45\)(nghìn đồng)
Giảm giá cho sản phẩm tối đa số phần trăm là: \(45\div150\times100\%=30\%\).

Ta có: \(\frac{x}{y+z}>\frac{x}{x+y+z};\frac{y}{x+z}>\frac{y}{x+y+z};\frac{z}{x+y}>\frac{z}{x+y+z}\)
\(\Rightarrow S>\frac{x+y+z}{x+y+z}=1\left(1\right)\)
+) Lại có: \(\frac{x}{y+z}< \frac{2x}{x+y+z};\frac{y}{x+z}< \frac{2y}{x+y+z};\frac{2z}{x+y+z}\)
\(\Rightarrow S< \frac{2\left(x+y+z\right)}{x+y+z}=2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow1< S< 2\)

Câu 1 :
Số khẩu trang khối 8, 9 dự định quyên góp theo kh lần lượt là x , y ( chiếc ) ( x , y \(\in\)N* ; x , y < 1140 )
Theo đề bài ta có PT : x + y = 1140 (1)
Thực tế, khối 8 quyên góp đc : x + 10%x = 1,1 x ( chiếc)
Thực tế, khối 9 quyên góp đc : y + 20%y = 1,2 y ( chiếc )
Theo đề bài ta có PT : 1,1 x + 1,2 y = 1314 (2)
Từ (1) và (2) ta có hệ PT :
\(\hept{\begin{cases}x+y=1140\\1,1x+1,2y=1314\end{cases}}\)
Giải tiếp hệ là ra nhé


\(x^2+ax+b+1=0\)
\(\Delta=a^2-4b-4\)
Để pt có 2 nghiệm pb \(\Leftrightarrow\Delta>0\Leftrightarrow a^2-4b-4>0\)
Theo hệ thức Vi-et ta có: \(\hept{\begin{cases}x_1+x_2=-a\\x_1.x_2=b+1\end{cases}}\)
Ta có: \(\hept{\begin{cases}x_1-x_2=3\\x_1^3-x_2^3=9\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1-x_2=3\\\left(x_1-x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)=9\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1-x_2=3\\x_1^2+x_1x_2+x_2^2=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1-x_2=3\\\left(x_1-x_2\right)^2+3x_1x_2=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1-x_2=3\\x_1x_2=-2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1=3+x_2\\\left(3+x_2\right)x_2=-2\left(1\right)\end{cases}}\)
\(\left(1\right)\Leftrightarrow x_2^2+3x_2+2=0\)
\(\Delta=1\)
\(\Rightarrow\)pt có 2 nghiệm pb \(\orbr{\begin{cases}x_2=\frac{-3+1}{2}=-1\Rightarrow x_1=2\\x_2=\frac{-3-1}{2}=-2\Rightarrow x_1=1\end{cases}}\)
TH1: \(x_1=2;x_2=-1\)
\(\Rightarrow\hept{\begin{cases}a=-1\\b=-3\end{cases}}\)( LOẠI vì a^2 -4b-4 <0 )
TH2: \(x_1=1;x_2=-2\)
\(\Rightarrow\hept{\begin{cases}a=1\\b=-3\end{cases}}\)( tm )
VẬY ...

Áp dụng Bđt cauchy-schwarz dạng đa thức cho 3 bộ số ta có;
\(\left(1.\sqrt{p-a}+1.\sqrt{p-b}+1.\sqrt{p-c}\right)^2\le\)
\(\left(1^2+1^2+1^2\right)\left[\left(\sqrt{p-a}\right)^2+\left(\sqrt{p-b}\right)^2+ \left(\sqrt{p-c}\right)^2\right]\)
\(=3\left(p-a+p-b+p-c\right)=3\left(3p-a-b-c\right)=3\left(3p-2p\right)=3p\)
\(\Rightarrow\sqrt{p-a}+\sqrt{p-b}+\sqrt{p-c}\le\sqrt{3p}\left(đpcm\right)\)
Dấu '=' xảy ra khi và chỉ khi a=b=c hay tam giác đó là tam giác đều



Câu 1 :
Do đường thẳng đi qua gốc tọa độ nên
Thay x = 0 ; y = 0 vào đường thẳng trên ta được
\(m^2-2m=0\Leftrightarrow m\left(m-2\right)=0\Leftrightarrow m=0;m=2\)
Vậy với m = 0 ; m =2 thì đường thẳng trên đi qua gốc tọa độ
Bài 2 đề sai rồi, đề làm gì phức tạp thế
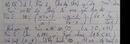
Để thu lợi nhuận ít nhất \(5\%\)thì giá bán tối thiểu là: \(100.\left(1+5\%\right)=105\)(nghìn đồng)
Giá giảm tối đa số tiền là: \(150-105=45\)(nghìn đồng)
Giảm giá cho sản phẩm tối đa số phần trăm là: \(45\div150\times100\%=30\%\).