-3/7 x 5/7+ -5/7 x 8/11+19/7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`#3107.101107`
c)
$-x + \dfrac{3}2 = x + \dfrac{3}5$
$\Rightarrow -x - x = \dfrac{3}5 - \dfrac{3}2$
$\Rightarrow -2x = -\dfrac{9}{10}$
$\Rightarrow 2x = \dfrac{9}{10}$
$\Rightarrow x = \dfrac{9}{10} \div 2$
$\Rightarrow x = \dfrac{9}{20}$
Vậy, $x = \dfrac{9}{20}.$

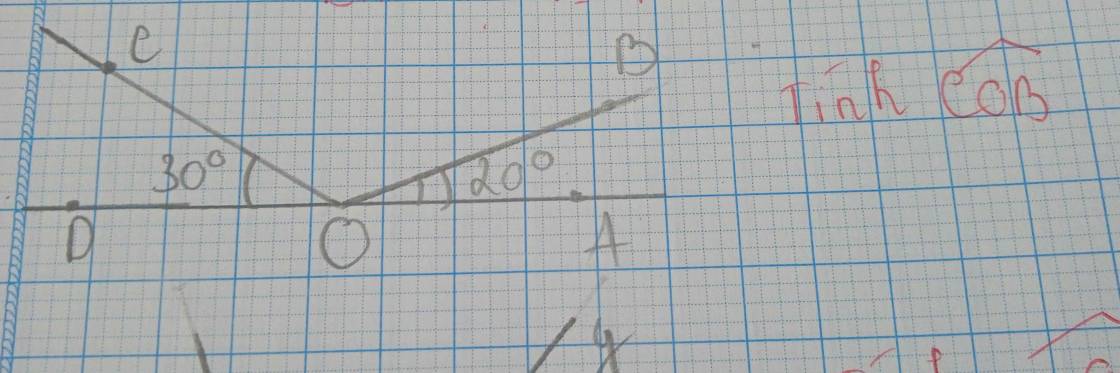
Ta có:
∠COD + ∠COB + ∠BOA = 180⁰
⇒ ∠COB = 180⁰ - (∠COD + ∠BOA)
= 180⁰ - (30⁰ + 20⁰)
= 180⁰ - 50⁰
= 130⁰

Lời giải:
Đặt $\frac{x}{2018}=\frac{y}{2019}=\frac{z}{2020}=a$
$\Rightarrow x=2018a; y=2019a; z=2020a$
$\Rightarrow (x-z)^3=(2018a-2020a)^3=(-2a)^3=-8a^3(1)$
Mặt khác:
$8(x-y)^2(y-z)=8(2018a-2019a)^2(2019a-2020a)=8a^2.(-a)=-8a^3(2)$
Từ $(1); (2)$ ta có đpcm.

a) \(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{26\cdot31}\)
\(=1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{26}-\dfrac{1}{31}\)
\(=1-\dfrac{1}{31}\)
\(=\dfrac{30}{31}\)
b) \(\dfrac{4}{11\cdot16}+\dfrac{4}{16\cdot21}+...+\dfrac{4}{61\cdot66}\)
\(=\dfrac{4}{5}\cdot\left(\dfrac{5}{11\cdot16}+\dfrac{5}{16\cdot21}+...+\dfrac{5}{61\cdot66}\right)\)
\(=\dfrac{4}{5}\cdot\left(\dfrac{1}{11}-\dfrac{1}{16}+\dfrac{1}{16}-...+\dfrac{1}{61}-\dfrac{1}{66}\right)\)
\(=\dfrac{4}{5}\cdot\left(\dfrac{1}{11}-\dfrac{1}{66}\right)\)
\(=\dfrac{4}{5}\cdot\dfrac{5}{66}\)
\(=\dfrac{4}{66}\)
\(=\dfrac{2}{33}\)
a) A = 5²/(1.6) + 5²/(6.11) + ... + 5²/(26.31)
= 5.[5/(1.6) + 5/(6.11) + ...+ 5/(26.31)]
= 5.(1 - 1/6 + 1/6 - 1/11 + ... + 1/26 - 1/31)
= 5.(1 - 1/31)
= 5.30/31
= 150/31
b) B = 4/(11.16) + 4/(16.21) + ... + 4/(61.66)
= 4/5 .[5/(11.16) + 5/(16.21) + ... + 5/(61.66)]
= 4/5.(1/11 - 1/16 + 1/16 - 1/21 + ... + 1/61 - 1/66)
= 4/5.(1/11 - 1/66)
= 4/5 . 5/66
= 2/33

Ta có:
\(A=\left(\dfrac{1}{2}-1\right)\cdot\left(\dfrac{1}{3}-1\right)\cdot\left(\dfrac{1}{4}-1\right)...\left(\dfrac{1}{10}-1\right)\)
\(A=-\dfrac{1}{2}\cdot-\dfrac{2}{3}-\dfrac{3}{4}\cdot...\cdot-\dfrac{9}{10}\)
\(A=\dfrac{-1\cdot-2\cdot-3\cdot...\cdot-9}{2\cdot3\cdot4\cdot...\cdot10}\)
\(A=-\dfrac{1}{10}\)
Mà: \(10>9\)
\(\Rightarrow\dfrac{1}{10}< \dfrac{1}{9}\)
\(\Rightarrow-\dfrac{1}{10}>-\dfrac{1}{9}\)
\(\Rightarrow A>-\dfrac{1}{9}\)

\(C=\dfrac{4}{1.3}.\dfrac{9}{2.4}.\dfrac{16}{3.5}.\dfrac{25}{4.6}....\dfrac{9801}{9800}=\)
\(=\dfrac{2^2.3^2.4^2.5^2.....99^2}{1.2.3^2.4^2.5^2....98^2.99.100}=\dfrac{2.99}{100}=\dfrac{198}{100}=1,98\)
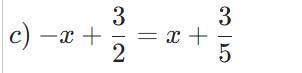

chỉ với
\(-\dfrac{3}{7}.\dfrac{5}{7}+\left(-\dfrac{5}{7}\right).\dfrac{8}{11}+\dfrac{19}{7}\\ =\dfrac{5}{7}.\left(-\dfrac{3}{7}-\dfrac{8}{11}\right)+\dfrac{19}{7}\\ =\dfrac{5}{7}.-\dfrac{89}{77}+\dfrac{19}{7}\\ =\dfrac{445}{539}+\dfrac{19}{7}\\ =\dfrac{1908}{539}\)