 giúp em bài này với em cảm ơn ạ
giúp em bài này với em cảm ơn ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


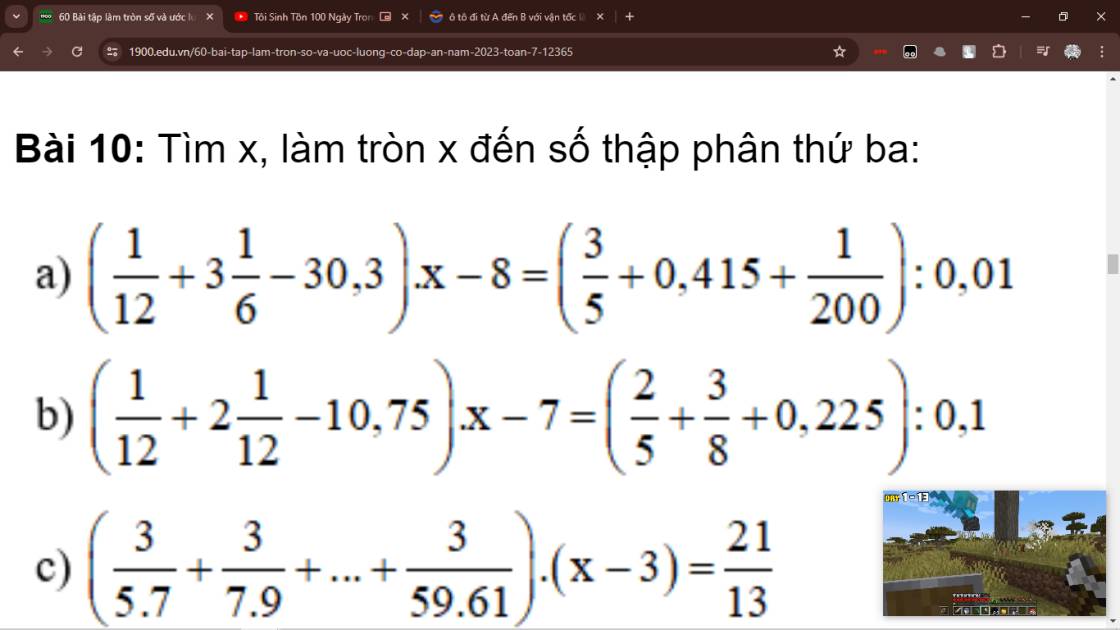
Bài 10:
\(A=\dfrac{2^{12}\cdot3^5-4^6\cdot81}{\left(2^2\cdot3\right)^6+8^4\cdot3^5}\\ =\dfrac{2^{12}\cdot3^5-\left(2^2\right)^6\cdot3^4}{\left(2^2\right)^6\cdot3^6+\left(2^3\right)^4\cdot3^5}\\ =\dfrac{2^{12}\cdot3^5-2^{12}\cdot3^4}{2^{12}\cdot3^6+2^{12}\cdot3^5}\\ =\dfrac{2^{12}\cdot3^4\cdot\left(3-1\right)}{2^{12}\cdot3^5\cdot\left(3+1\right)}\\ =\dfrac{3-1}{3\cdot\left(3+1\right)}\\ =\dfrac{2}{3\cdot4}\\ =\dfrac{1}{6}\)
\(B=\dfrac{30\cdot4^7\cdot3^{29}-5\cdot14^5\cdot2^{12}}{54\cdot6^{14}\cdot9^7-12\cdot8^5\cdot7^5}\\ =\dfrac{2\cdot3\cdot5\cdot\left(2^2\right)^7\cdot3^{29}-5\cdot2^5\cdot7^5\cdot2^{12}}{2\cdot3^3\cdot2^{14}\cdot3^{14}\cdot\left(3^2\right)^7-2^2\cdot3\cdot\left(2^3\right)^5\cdot7^5\cdot}\\ =\dfrac{3^{30}\cdot2^{15}\cdot5-5\cdot2^{17}\cdot7^5}{2^{15}\cdot3^{17}\cdot3^{14}-2^{17}\cdot7^5\cdot3}\\ =\dfrac{3^{30}\cdot2^{15}\cdot5-5\cdot2^{17}\cdot7^5}{2^{15}\cdot3^{31}-2^{17}\cdot7^5\cdot3}\\ =\dfrac{5\cdot\left(3^{30}\cdot2^{15}-2^{17}\cdot7^5\right)}{3\cdot\left(2^{15}\cdot3^{30}-2^{17}\cdot7^5\right)}\\ =\dfrac{5}{3}\)
Bài 8:
\(\left\{{}\begin{matrix}x+y=\dfrac{1}{2}\\y+z=\dfrac{1}{3}\\x+z=\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=\dfrac{1}{2}\\y=\dfrac{1}{3}-z\\x=\dfrac{1}{6}-z\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{3}-z+\dfrac{1}{6}-z=\dfrac{1}{2}\\y=\dfrac{1}{3}-z\\x=\dfrac{1}{6}-z\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2}-2z=\dfrac{1}{2}\\y=\dfrac{1}{3}-z\\x=\dfrac{1}{6}-z\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2z=0\\y=\dfrac{1}{3}-z\\x=\dfrac{1}{6}-z\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}z=0\\y=\dfrac{1}{3}-0=\dfrac{1}{3}\\x=\dfrac{1}{6}-0=\dfrac{1}{6}\end{matrix}\right.\)
Bài 5:
\(A=\left(\dfrac{3}{2}-\dfrac{2}{5}+\dfrac{1}{10}\right):\left(\dfrac{3}{2}-\dfrac{2}{3}+\dfrac{1}{12}\right)\)
\(=\dfrac{15-4+1}{10}:\dfrac{9-4+1}{12}\)
\(=\dfrac{12}{10}\cdot\dfrac{12}{6}=\dfrac{6}{5}\cdot2=\dfrac{12}{5}\)

\(S=1+2+2^2+2^3+...+2^{2009}+2^{2008}\\ 2S=2\left(1+2+2^2+...+2^{2008}\right)\\ 2S=2+2^2+2^3+...+2^{2009}\\ 2S-S=\left(2+2^2+2^3+...+2^{2009}\right)-\left(1+2+2^2+...+2^{2008}\right)\\ S=2^{2009}-1\)

\(-\dfrac{25}{20}>0\)
\(\dfrac{20}{25}>0\)
\(\Rightarrow-\dfrac{25}{20}< \dfrac{20}{25}\)

\(\dfrac{x}{7}+\dfrac{2}{y}=\dfrac{-1}{15}\)
=>\(\dfrac{xy+14}{7y}=\dfrac{-1}{15}\)
=>\(15\left(xy+14\right)+7y=0\)
=>\(15xy+7y=-210\)
=>y(15x+7)=-210
mà 15x+7 chia 15 dư 7
nên \(\left(15x+7;y\right)\in\left\{\left(7;-30\right)\right\}\)
=>\(\left(x;y\right)\in\left(0;-30\right)\)

a) \(x-\dfrac{3}{5}=\dfrac{2}{7}\)
\(\Rightarrow x=\dfrac{2}{7}+\dfrac{3}{5}\)
\(\Rightarrow x=\dfrac{10}{35}+\dfrac{21}{35}\)
\(\Rightarrow x=\dfrac{31}{35}\)
b) \(x+\dfrac{20}{11\cdot13}+\dfrac{20}{13\cdot15}+...+\dfrac{20}{53\cdot55}=\dfrac{3}{11}\)
\(\Rightarrow x+10\left(\dfrac{2}{11\cdot13}+\dfrac{2}{13\cdot15}+...+\dfrac{2}{53\cdot55}\right)=\dfrac{3}{11}\)
\(\Rightarrow x+10\left(\dfrac{1}{11}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{15}+...+\dfrac{1}{53}-\dfrac{1}{55}\right)=\dfrac{3}{11}\)
\(\Rightarrow x+10\left(\dfrac{1}{11}-\dfrac{1}{55}\right)=\dfrac{3}{11}\)
\(\Rightarrow x+10\cdot\dfrac{4}{55}=\dfrac{3}{11}\)
\(\Rightarrow x+\dfrac{40}{55}=\dfrac{3}{11}\)
\(\Rightarrow x=\dfrac{3}{11}-\dfrac{40}{55}\)
\(\Rightarrow x=\dfrac{-25}{55}=\dfrac{-5}{11}\)

a)
\(\dfrac{4}{5}-\left(\dfrac{-2}{3}\right)-\dfrac{1}{10}-\dfrac{2}{3}\\ =\dfrac{4}{5}+\dfrac{2}{3}-\dfrac{1}{10}-\dfrac{2}{3}\\ =\left(\dfrac{4}{5}-\dfrac{1}{10}\right)+\left(\dfrac{2}{3}-\dfrac{2}{3}\right)\\ =\dfrac{7}{10}+0\\ =\dfrac{7}{10}\)
b)
\(\dfrac{1}{3}-\dfrac{-1}{2}+\dfrac{1}{13}-\dfrac{5}{6}\\ =\left(\dfrac{1}{2}+\dfrac{1}{3}\right)+\dfrac{1}{13}-\dfrac{5}{6}\\ =\dfrac{5}{6}+\dfrac{1}{13}-\dfrac{5}{6}\\ =\dfrac{1}{13}\)
c)
\(\dfrac{-5}{12}-\left(\dfrac{-5}{6}-\dfrac{5}{12}\right)\\ =\dfrac{-5}{12}+\dfrac{5}{6}+\dfrac{5}{12}\\ =\left(-\dfrac{5}{12}+\dfrac{5}{12}\right)+\dfrac{5}{6}\\ =\dfrac{5}{6}\)

\(\left(\dfrac{1}{2}-1\right).\left(\dfrac{1}{3}-1\right).\left(\dfrac{1}{4}-1\right)...\left(\dfrac{1}{2008}-1\right).\left(\dfrac{1}{2009}-1\right)\)
\(=-\dfrac{1}{2}.-\dfrac{2}{3}.-\dfrac{3}{4}...-\dfrac{2007}{2008}.-\dfrac{2008}{2009}\)
\(=-\left(\dfrac{1.2.3...2007.2008}{2.3.4...2008.2009}\right)\)
\(=-\dfrac{1}{2009}\)

\(\dfrac{x+4}{2000}+\dfrac{x+3}{2001}=\dfrac{x+2}{2002}+\dfrac{x+1}{2003}\)
\(\Leftrightarrow\dfrac{x+4}{2000}+1+\dfrac{x+3}{2001}+1=\dfrac{x+2}{2002}+1+\dfrac{x+1}{2003}+1\)
\(\Leftrightarrow\dfrac{x+2004}{2000}+\dfrac{x+2004}{2001}=\dfrac{x+2004}{2002}+\dfrac{x+2004}{2003}\)
\(\Leftrightarrow\left(x+2004\right)\left(\dfrac{1}{2000}+\dfrac{1}{2001}-\dfrac{1}{2002}-\dfrac{1}{2003}\right)=0\Leftrightarrow x=-2004\)
\(\dfrac{x+4}{2000}+\dfrac{x+3}{2001}=\dfrac{x+2}{2002}+\dfrac{x+1}{2003}\)
=>\(\left(\dfrac{x+4}{2000}+1\right)+\left(\dfrac{x+3}{2001}+1\right)=\left(\dfrac{x+2}{2002}+1\right)+\left(\dfrac{x+1}{2003}+1\right)\)
=>\(\dfrac{x+2004}{2000}+\dfrac{x+2004}{2001}=\dfrac{x+2004}{2002}+\dfrac{x+2004}{2003}\)
=>\(\left(x+2004\right)\left(\dfrac{1}{2000}+\dfrac{1}{2001}-\dfrac{1}{2002}-\dfrac{1}{2003}\right)=0\)
=>x+2004=0
=>x=-2004

Người thợ săn trộn số lít sơn xanh và trắng là :
3,8 + 0,7 = 4,5 ( l )
Người thợ sơn còn lại số lít sơn xanh nhạt là :
4,5 - 1,25 = 3,25 ( l )
Đáp số : 3,25l sơn xanh nhạt



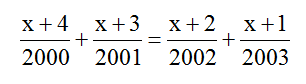
a)
\(\left(\dfrac{1}{12}+3\dfrac{1}{6}-30,3\right)x-8=\left(\dfrac{3}{5}+0,415+\dfrac{1}{200}\right):0,01\\ \Rightarrow\left(\dfrac{1}{12}+\dfrac{19}{6}-\dfrac{303}{10}\right)x-8=\left(\dfrac{3}{5}+0,415+\dfrac{1}{200}\right)\cdot100\\ \Rightarrow-\dfrac{541}{20}x-8=\dfrac{51}{50}\cdot100\\ \Rightarrow-\dfrac{541}{20}x-8=102\\ \Rightarrow-\dfrac{541}{20}x=110\\ \Rightarrow x=110:-\dfrac{541}{20}\\\Rightarrow x=-\dfrac{2200}{541}\approx4,067\)
b)
\(\left(\dfrac{1}{12}+2\dfrac{1}{12}-10,75\right)x-7=\left(\dfrac{2}{5}+\dfrac{3}{8}+0,225\right):0,1\\ \Rightarrow\left(\dfrac{1}{12}+\dfrac{25}{12}-\dfrac{43}{4}\right)x-7=\left(\dfrac{2}{5}+\dfrac{3}{8}+\dfrac{9}{40}\right)\cdot10\\ \Rightarrow-\dfrac{103}{12}x=1\cdot10\\ \Rightarrow x=10:-\dfrac{103}{12}\\ \Rightarrow x=-\dfrac{120}{103}\\ \Rightarrow x\approx-1,165\)
c)
\(\left(\dfrac{3}{5\cdot7}+\dfrac{3}{7\cdot9}+...+\dfrac{3}{59\cdot61}\right)\left(x-3\right)=\dfrac{21}{13}\\ \Rightarrow\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+...+\dfrac{2}{59\cdot61}\right)\left(x-3\right)=\dfrac{21}{13}\\ \Rightarrow\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{59}-\dfrac{1}{61}\right)\left(x-3\right)=\dfrac{21}{13}\\\Rightarrow \dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{61}\right)\left(x-3\right)=\dfrac{21}{13}\\ \Rightarrow\dfrac{84}{305}\left(x-3\right)=\dfrac{21}{13}\\ \Rightarrow x-3=\dfrac{21}{13}:\dfrac{84}{305}\\ \Rightarrow x-3=\dfrac{305}{52}\\ \Rightarrow x=\dfrac{305}{52}+3\\ \Rightarrow x=\dfrac{461}{52}\\ \Rightarrow x\approx8,865\)