điểm -5 cách điểm 0: đơn vị
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





B = \(\dfrac{2-3x}{x+1}\) (đk \(x\) ≠ -1)
Vì B \(\in\) P nên
2 - 3\(x\) ⋮ \(x\) + 1
- 3(\(x\) + 1) + 5 ⋮ \(x\) + 1
5 ⋮ \(x\) + 1
\(x\) + 1 \(\in\) Ư(5) = {-5; -1; 1; 5}
Lập bảng ta có:
| \(x\) + 1 | -5 | -1 | 1 | 5 |
| \(x\) | -6 | -2 | 0 | 4 |
| B = \(\dfrac{2-3x}{x+1}\) | -4 | -8 | 2 | -2 |
| loại | loại | loại |
Theo bảng trên ta có: \(x\) = 0
Kết luận: Để B = \(\dfrac{2-3x}{x+1}\) là số nguyên tố thì \(x\) = 0
ĐKXĐ: x<>-1
Để B là số nguyên thì \(-3x+2⋮x+1\)
=>\(-3x-3+5⋮x+1\)
=>\(5⋮x+1\)
=>\(x+1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{0;-2;4;-6\right\}\)
Thay x=0 vào B, ta được:
\(B=\dfrac{2-3\cdot0}{0+1}=\dfrac{2}{1}=2\) là số nguyên tố
=>Nhận
Thay x=-2 vào B, ta được:
\(B=\dfrac{2-3\cdot\left(-2\right)}{-2+1}=\dfrac{2+6}{-1}=-8\) không là số nguyên tố
=>Loại
THay x=4 vào B, ta được:
\(B=\dfrac{2-3\cdot4}{4+1}=\dfrac{-10}{5}=-2\) không là số nguyên tố
=>Loại
Thay x=-6 vào B, ta được:
\(B=\dfrac{2-3\cdot\left(-6\right)}{-6+1}=\dfrac{2+18}{-5}=\dfrac{20}{-5}=-4\) không là số nguyên tố
=>Loại

Bài 1:
a: \(2020\left(-2021\right)+2020\cdot1021\)
\(=2020\left(-2021+1021\right)\)
\(=2020\cdot\left(-1000\right)=-2020000\)
b: \(\dfrac{-5}{21}+\dfrac{8}{24}+\dfrac{-2}{21}\)
\(=\left(\dfrac{-5}{21}-\dfrac{2}{21}\right)+\dfrac{8}{24}\)
\(=-\dfrac{7}{21}+\dfrac{8}{24}=-\dfrac{1}{3}+\dfrac{1}{3}=0\)
Bài 2:
a: \(x-\dfrac{1}{11}=-\dfrac{12}{11}\)
=>\(x=-\dfrac{12}{11}+\dfrac{1}{11}\)
=>\(x=-\dfrac{11}{11}=-1\)
b: \(\dfrac{3}{2}-x=\dfrac{4}{5}+\dfrac{-2}{3}\)
=>\(\dfrac{3}{2}-x=\dfrac{12-10}{15}=\dfrac{2}{15}\)
=>\(x=\dfrac{3}{2}-\dfrac{2}{15}=\dfrac{45-4}{30}=\dfrac{41}{30}\)

\(\dfrac{x-3}{32}=\dfrac{-2}{3-x}\)
\(\Rightarrow\dfrac{x-3}{32}=\dfrac{-\left(-2\right)}{-\left(3-x\right)}\)
\(\Rightarrow\dfrac{x-3}{32}=\dfrac{2}{x-3}\)
\(\Rightarrow\left(x-3\right)^2=64\)
\(\Rightarrow\left[{}\begin{matrix}x-3=8\\x-3=-8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=11\\x=-5\end{matrix}\right.\)
\(x-\dfrac{3}{32}=-\dfrac{2}{3}-x\\ \Rightarrow x-\dfrac{3}{32}+x=-\dfrac{2}{3}\\ \Rightarrow2x=-\dfrac{55}{96}\\ \Rightarrow x=-\dfrac{55}{192}.\)

\(\dfrac{x-2}{-3}=\dfrac{-27}{x-2}\)
\(\Rightarrow\left(x-2\right)^2=81\)
\(\Rightarrow\left[{}\begin{matrix}x-2=9\\x-2=-9\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=11\\x=-7\end{matrix}\right.\)
P/s: Bạn chú ý lần sau hỏi bài thì bạn nên soạn vào ô "\(\Sigma\)" ở bên trái nhe(Ban đầu mik còn tưởng đề là \(x-\dfrac{2}{-3}=-\dfrac{27}{x}-2\) chứ)

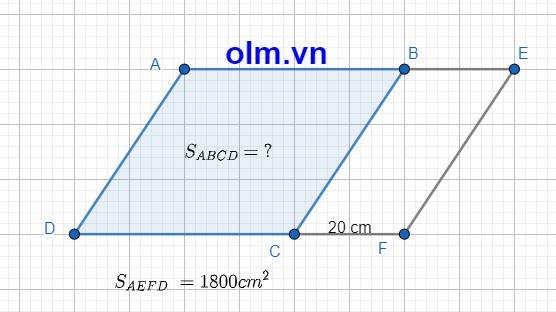
Hình thoi cũng là hình bình hành nên công thức tính diện tích hình bình hành cũng là công thức tính diện tích hình thoi. Từ lập luận trên ta có:
Tỉ số diện tích hình thoi ABCD và diện tích hình binh hành BEFC là :
\(\dfrac{DC}{CF}\) (Vì hai hình bình hành có chung chiều cao hạ từ đỉnh B xuống đáy DF)
DC = 16 : 4 = 4 (dm)
4 dm = 40 cm
\(\dfrac{S_{ABCD}}{S_{BEFC}}\) = 40 : 20 = 2
⇒ SBEFC =\(\dfrac{1}{2}\)SABCD
⇒ SAEFD = SABCD + \(\dfrac{1}{2}\)SABCD = \(\dfrac{3}{2}\)SABCD
SABCD = 1800 : \(\dfrac{3}{2}\) = 1200 (cm2)
Kết luận diện tích hình thoi là: 1200 cm2

Nếu k là số lẻ thì 15k + 1 là số chẵn hay 15k + 1 là hợp số.
Nếu k là số chẵn thì 15k + 1 có thể là hợp số cũng có thể là số nguyên tố.
Với mọi k \(\in\) N thì 15k + 1 là hợp số hay nguyên tố chưa thể xác định được.
Điểm -5 cách điểm 0 số đơn vị là:
|0-(-5)|=5(đơn vị)
cách 5 đơn vị