mình cần gấp ạ, tối nay mình cần nôpj r ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nửa chu vi của hình chữ nhật là: 60:2=30(m)
Chiều rộng của hình chữ nhật là: (30-6):2=12(m)
Chiều dài của hình chữ nhật là: 30 - 12 = 18(m)
Diện tích mảnh đất là: 18 x 12 = 216 (m2)
Đáp số: 216m2
Giải:
Nửa chu vi của mảnh vườn hình chữ nhật là:
60 : 2 = 30 (m)
Gọi chiều rộng lúc đầu của mảnh vườn hình chữ nhật là \(x\) (m); 30 > \(x\) > 0
Chiều dài lúc đầu của mảnh vườn hình chữ nhật là: 30 - \(x\) (m)
Chiều dài của mảnh vườn hình chữ nhật lúc sau là:
30 - \(x\) + 2 = (30 + 2) - \(x\) = 32 - \(x\) (m)
Chiều rộng của hình chữ nhật lúc sau là: \(x\) + 6 (m)
Diện tích của hình chữ nhật lúc sau là:
(32 - \(x\))(\(x\) + 6) (m2)
Diện tích của mảnh vườn hình chữ nhật lúc đầu là: (30 - \(x\)) x \(x\) = 30\(x\) - \(x^2\) (m2)
Theo bài ra ta có phương trình:
(32 - \(x\))(\(x\) + 6) - (30\(x\) - \(x^2\)) = 96
32\(x\) + 192 - \(x^2\) - 6\(x\) - 30\(x\) + \(x^2\) = 96
(32\(x\) - 6\(x\) - 30\(x\)) + 192 - (\(x^2\) - \(x^2\)) = 96
(26\(x\) - 30\(x\)) + 192 + 0 = 96
- 4\(x\) + 192 = 96
4\(x\) = 192 - 96
4\(x\) = 96
\(x\) = 96 : 4
\(x\) = 24
Chiều dài ban đầu của hình chữ nhật là: 30 - 24 = 6 (m)
6 < 24
Chiều dài nhỏ hơn chiều rộng, không có hình chữ nhật nào có kích thước thoả mãn đề bài.
S = \(\dfrac{3}{2}\)+ \(\dfrac{7}{6}\)+\(\dfrac{13}{12}\)+...+\(\dfrac{9901}{9900}\)
Xin giúp với!!!

\(S=\dfrac{3}{2}+\dfrac{7}{6}+\dfrac{13}{12}+...+\dfrac{9901}{9900}\)
\(=1+\dfrac{1}{2}+1+\dfrac{1}{6}+...+1+\dfrac{1}{9900}\)
\(=\left(1+1+1+...+1\right)+\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\right)\)
\(=99+\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(=99+\left(1-\dfrac{1}{100}\right)=100-\dfrac{1}{100}=\dfrac{10000-1}{100}=\dfrac{9999}{100}\)
S = ( 1+\(\dfrac{1}{2}\) ) + ( 1 + \(\dfrac{1}{6}\) ) + .... + ( 1 + \(\dfrac{1}{9900}\) )
= 9900 + ( \(\dfrac{1}{1.2}\) + \(\dfrac{1}{2.3}\) + ..... + \(\dfrac{1}{99.100}\) )
= 9900 + ( 1 - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + ..... + \(\dfrac{1}{99}\) - \(\dfrac{1}{100}\) )
= 9900 + 1 - \(\dfrac{1}{100}\)
= 9901 - \(\dfrac{1}{100}\)

Tam giác ABC vuông tại A ta có:
\(tanB=\dfrac{AC}{AB}=>\dfrac{5}{12}=\dfrac{AC}{6}=>AC=\dfrac{5\cdot6}{12}=\dfrac{5}{2}\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(AB^2+AC^2=BC^2\\ =>BC=\sqrt{AB^2+AC^2}\\ =>BC=\sqrt{6^2+\left(\dfrac{5}{2}\right)^2}=\dfrac{13}{2}\left(cm\right)\)
Để giải bài toán, ta cần sử dụng một số công thức và định lý trong hình học, đặc biệt là định lý Pythagore và định nghĩa của các hàm số lượng giác.
Cho tam giác ABC vuông tại A, với AB = 6 cm và tanα = 5/12. Góc B = α.
a) Tính độ dài cạnh AC
Vì tam giác vuông tại A, góc α là góc B, ta có:
tan(α)=đoˆˊi diệnkeˆˋ\tan(\alpha) = \frac{\text{đối diện}}{\text{kề}}tan(α)=keˆˋđoˆˊi diện
Trong tam giác ABC vuông tại A:
tan(α)=BCAC\tan(\alpha) = \frac{BC}{AC}tan(α)=ACBC
Theo đề bài, tan(α)=512\tan(\alpha) = \frac{5}{12}tan(α)=125.
Do đó, ta có:
BCAC=512\frac{BC}{AC} = \frac{5}{12}ACBC=125
Từ đó suy ra:
BC=512ACBC = \frac{5}{12} ACBC=125AC
b) Tính độ dài cạnh BC
Ta sử dụng định lý Pythagore cho tam giác ABC vuông tại A:
BC2=AB2+AC2BC^2 = AB^2 + AC^2BC2=AB2+AC2
Đầu tiên, ta cần tính AC.
Biết rằng tan(α)=512\tan(\alpha) = \frac{5}{12}tan(α)=125, do đó ta có:
sin(α)=BCBC2+AC2\sin(\alpha) = \frac{BC}{BC^2 + AC^2}sin(α)=BC2+AC2BC sin(α)=BCBC2+AC2\sin(\alpha) = \frac{BC}{BC^2 + AC^2}sin(α)=BC2+AC2BC
Vì tan(α) = 5/12 nên ta đặt BC = 5k và AC = 12k. Vì thế:
BC=5kBC = 5kBC=5k
AC=12kAC = 12kAC=12k
Sử dụng định lý Pythagore:
BC2=AB2+AC2BC^2 = AB^2 + AC^2BC2=AB2+AC2
(5k)2=AB2+(12k)2(5k)^2 = AB^2 + (12k)^2(5k)2=AB2+(12k)2
25k2=62+144k225k^2 = 6^2 + 144k^225k2=62+144k2
25k2=36+144k225k^2 = 36 + 144k^225k2=36+144k2
Từ đó, ta có:
AC=12k5AC = \frac{12k}{5}AC=512k
AC2=AB2+BC2AC^2 = AB^2 + BC^2AC2=AB2+BC2
(12k)2=62+(5k)2(12k)^2 = 6^2 + (5k)^2(12k)2=62+(5k)2
144k2=36+25k2144k^2 = 36 + 25k^2144k2=36+25k2
144k2−25k2=36144k^2 - 25k^2 = 36144k2−25k2=36
119k2=36119k^2 = 36119k2=36
k2=36119k^2 = \frac{36}{119}k2=11936
k=36119k = \sqrt{\frac{36}{119}}k=11936
k=6119k = \frac{6}{\sqrt{119}}k=1196
BC=5k=5×6119=30119BC = 5k = 5 \times \frac{6}{\sqrt{119}} = \frac{30}{\sqrt{119}}BC=5k=5×1196=11930
AC=12k=12×6119=72119AC = 12k = 12 \times \frac{6}{\sqrt{119}} = \frac{72}{\sqrt{119}}AC=12k=12×1196=11972
Chúng ta có thể tính toán lại bằng cách:
Suy ra: BC=512ACBC = \frac{5}{12} ACBC=125AC AC=12×65=14.4AC = \frac{12 \times 6}{5} = 14.4AC=512×6=14.4 BC=5×1.2=6BC = 5 \times 1.2 = 6BC=5×1.2=6
Suy ra:...

Đây là toán nâng cao chuyên đề phân số, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải dạng này bằng phương pháp giải ngược như sau:
Giải:
Ngày thứ hai nếu anh chỉ tiêu \(\dfrac{1}{2}\) số tiền mà không ủng hộ từ thiện thêm 60 000 đồng thì anh còn lại số tiền là:
0 + 60 000 = 60 000 (đồng)
60 000 đồng ứng với phân số là:
1 - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\) (số tiền còn lại sau ngày thứ nhất)
Số tiền còn lại sau ngày thứ nhất là:
60 000 : \(\dfrac{1}{2}\) = 120 000 (đồng)
Nếu ngày thứ nhất anh tiêu thêm 20 000 đồng nữa thì số tiền còn lại là:
120 000 - 20 000 = 100 000 (đồng)
100 000 đồng ứng với phân số là:
1 - \(\dfrac{1}{3}\) = \(\dfrac{2}{3}\) (số tiền)
Ban đầu anh có số tiền là:
100 000 : \(\dfrac{2}{3}\) = 150 000 (đồng)
Đáp số: 150 000 đồng.

\(x^2+5y^2+2y-4xy-3=0\\ \Rightarrow\left(x^2-4xy+4y^2\right)+\left(y^2+2y+1\right)-4=0\\ \Rightarrow\left(x-2y\right)^2+\left(y+1\right)^2=4\)
Mình nghĩ bạn thiếu đề nhé
Bổ sung đề: Tìm cặp x, y nguyên thỏa mãn
Với x, y nguyên hiển nhiên x-2y và y+1 nguyên
Mà: \(4=0^2+2^2=0^2+\left(-2\right)^2\)
Các trường hợp xảy ra:
TH1: y+1=0 và x-2y=2
=> y=-1 và x=0
TH2: y+1=0 và x-2y=-2
=> y=-1 và x=-4
TH3: y+1=2 và x-2y=0
=> y=1 và x=2
TH4: y+1=-2 và x-2y=0
=> y=-3 và x=-6
Vậy (x;y)=(0;-1);(-4;-1);(2;1);(-6;-3)


a: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\) và \(MA\cdot MB=HM^2\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right);NA\cdot NC=NH^2\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\left(3\right);AB^2=BH\cdot BC;AC^2=CH\cdot BC\)
Từ (1) và (3) suy ra \(AM\cdot AB=HB\cdot HC\)
b: Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
c: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>\(HA^2=HM^2+HN^2\)
=>\(HB\cdot HC=MA\cdot MB+NA\cdot NC\)
d: \(\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot BC}=\dfrac{BH}{CH}\)
=>\(\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2\)
e: Xét ΔAHB vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\)
=>\(BM=\dfrac{BH^2}{BA}\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(CN\cdot CA=CH^2\)
=>\(CN=\dfrac{CH^2}{CA}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(BC=\dfrac{AB\cdot AC}{AH}\)
\(BM\cdot CN\cdot BC=\dfrac{BH^2}{BA}\cdot\dfrac{CH^2}{CA}\cdot\dfrac{AB\cdot AC}{AH}\)
\(=\dfrac{BH^2}{AH}\cdot CH^2=\dfrac{\left(BH\cdot CH\right)^2}{AH}=\dfrac{AH^4}{AH}=AH^3\)
mà AH=MN(AMHN là hình chữ nhật)
nên \(BM\cdot CN\cdot BC=MN^3\)
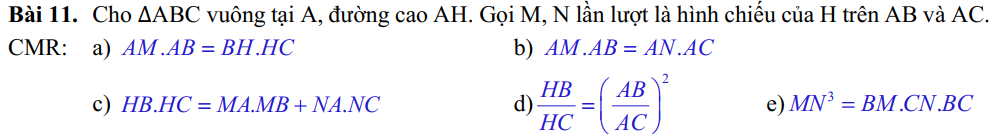
a) Ta có: \(\widehat{cNb}+\widehat{MNb}=180^{\circ}\) (hai góc kề bù)
\(\Rightarrow\widehat{MNb}=180^{\circ}-\widehat{cNb}=180^{\circ}-55^{\circ}=125^{\circ}\)
b) Ta có: \(\widehat{MNb}=\widehat{aMN}\left(=125^{\circ}\right)\)
Mà hai góc này đều nằm ở vị trí so le trong
Nên \(Ma//Nb\)