4, 5 - 2x) * 1 3/7 = - 17/14
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{15}{6}-\dfrac{3}{8}\)
\(=\dfrac{5}{2}-\dfrac{3}{8}\) (Đưa \(\dfrac{15}{6}\) về phân số tối giản)
\(=\dfrac{20}{8}-\dfrac{3}{8}\) (Quy đồng phân số \(\dfrac{5}{2}\))
\(=\dfrac{17}{8}\)

Giải:
Chiều cao của thửa ruộng hình thang lúc đầu là:
114 x 2 : 12 = 19 (m)
Diện tích thửa ruộng hình thang lúc đầu là:
34 x 19 = 456 (m2)
Đáp số: 456m2

\(25\%=\dfrac{25}{100}=\dfrac{1}{4}\)
\(2TK=200\) năm
\(=>25\%của2TK=\dfrac{1}{4}\) x \(200\)
\(=>50\)
Vậy 25% của 2 thế kỉ = 50 năm

Số cái bánh có thể mua:
1500000 : 250000 = 6 (cái)
Số phần bánh mỗi bạn được chia:
6 : 48 = 1/6 (cái bánh)

Số ngôi sao Minh tặng cho Nam là :
81 \(\times\) \(\dfrac{1}{3}\) = 27 ( ngôi sao )
Số ngôi sao Minh tặng cho Na là :
81 \(\times\) \(\dfrac{2}{9}\) = 18 ( ngôi sao )
Số ngôi sao Minh đã tặng cho tất cả hai bạn là :
27 + 18 = 45 ( ngôi sao )
Đáp số : 45 ngôi sao
Tick cho mik nhé, thanks
Số ngôi sao Minh gấp tặng Nam là : 81 x 1/3 = 27 ( ngôi sao)
Số ngôi sao Minh gấp tặng Na là : 81 x 2/9 = 18 ( ngôi sao)
Minh đã tặng tất cả hai bạn số ngôi sao là: 27 + 18 = 45 ( ngôi sao )
Đáp số : 45 ngôi sao
Tick cho chị nha :)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
b: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
=>HM=HN
mà HM<HB(ΔHMB vuông tại M)
nên HN<HB
c: Ta có: DH//AC
=>\(\widehat{DHA}=\widehat{HAC}\)
mà \(\widehat{HAC}=\widehat{HAB}\)
nên \(\widehat{DHA}=\widehat{DAH}\)
=>DA=DH
Ta có: \(\widehat{DAH}+\widehat{DBH}=90^0\)(ΔAHB vuông tại H)
\(\widehat{DHA}+\widehat{DHB}=90^0\)
mà \(\widehat{DAH}=\widehat{DHA}\)
nên \(\widehat{DBH}=\widehat{DHB}\)
=>DB=DH
mà DH=DA
nên DB=DA
=>D là trung điểm của AB
=>\(DH=\dfrac{1}{2}AB\)
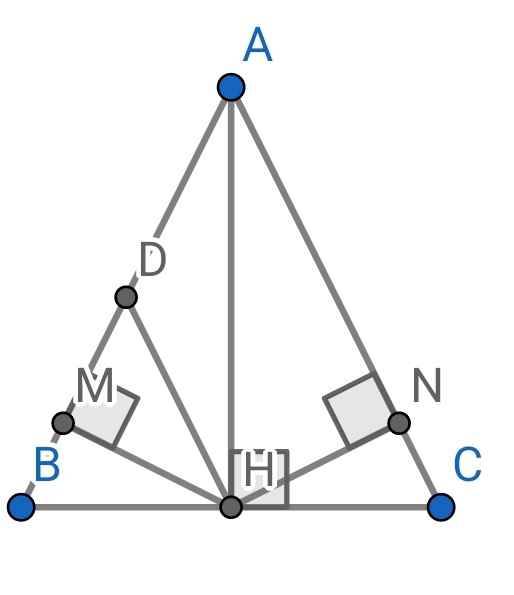
a) Do ∆ABC cân tại A (gt)
AH là đường cao (gt)
⇒ AH cũng là đường trung tuyến
⇒ H là trung điểm của BC
⇒ BH = HC
b) ∆CHN vuông tại N
⇒ CH là cạnh huyền nên là cạnh lớn nhất
⇒ CH > HN
Mà BH = CH (cmt)
⇒ BH > HN
c) ∆ABC cân tại A (gt)
AH là đường cao (gt)
⇒ AH là đường phân giác
⇒ ∠BAH = ∠CAH
⇒ ∠DAH = ∠CAH
Do HD // AC (gt)
⇒ ∠DHA = ∠CAH (so le trong)
Mà ∠DAH = ∠CAH (cmt)
⇒ ∠DHA = ∠DAH
⇒ ∆AHD cân tại D
⇒ DH = AD (1)
Do DH // AC (gt)
⇒ ∠DHB = ∠ACB (đồng vị)
Mà ∠ACB = ∠ABC (∆ABC cân tại A)
⇒ ∠DHB = ∠ABC
⇒ ∠DHB = ∠DBH
⇒ ∆BHD cân tại D
⇒ DH = BD (2)
Từ (1) và (2) ⇒ D là trung điểm của AB
⇒ DH = AD = BD = AB : 2

a: Xét ΔBAM vuông tại A và ΔBNM vuông tại Ncó
BM chung
\(\widehat{ABM}=\widehat{NBM}\)
Do đó: ΔBAM=ΔBNM
=>\(\widehat{AMB}=\widehat{NMB}\)
=>MB là phân giác của góc AMN
b: Ta có: NK//BM
=>\(\widehat{BMN}=\widehat{KNM}\)(hai góc so le trong)
mà \(\widehat{NKM}=\widehat{AMB}\)(hai góc đồng vị, BM//NK)
mà \(\widehat{BMN}=\widehat{AMB}\)
nên \(\widehat{KNM}=\widehat{NKM}\)
=>ΔMNK cân tại M
c: Ta có: ΔBAM=ΔBNM
=>BA=BN và MA=MN
BA=BN
=>B nằm trên đường trung trực của AN(1)
MA=MN
=>M nằm trên đường trung trực của AN(2)
Từ (1),(2) suy ra BM là đường trung trực của AN
=>BM\(\perp\)AN


\(4,5-2x.1\dfrac{3}{7}=\dfrac{17}{14}\)
\(\dfrac{9}{2}-2x.\dfrac{10}{7}=\dfrac{17}{14}\)
\(2x.\dfrac{10}{7}=\dfrac{9}{2}-\dfrac{17}{14}\)
\(2x.\dfrac{10}{7}=\dfrac{23}{7}\)
\(2x\) \(=\dfrac{23}{7}:\dfrac{10}{7}\)
\(2x\) \(=\dfrac{23}{10}\)
\(x\) \(=\dfrac{23}{10}:2\)
\(x\) \(=\dfrac{23}{20}\)