25% = 1/4

Số đường còn lại sau khi bán 25%:

1 - 1/4 = 3/4 (số đường)

Số đường bán trong ngày thứ hai:

4/9 . 3/4 = 1/3 (số đường)

Số đường ngày thứ ba bán được:

1 - 1/4 - 1/3 = 5/12 (số đường)

Tỉ số đường bán được của ngày thứ ba và ngày thứ nhất:

5/12 : 1/4 = 5/3

Ngày thứ nhất bán được số kg đường là:

120.25%=30120.25%=30 (kg đường)

Sau ngày thứ nhất, số đường còn lại là:

120−30=90120−30=90 (kg)

Ngày thứ hai bán được số kg đường là:

90.49=4090.94​=40 (kg)

Ngày thứ ba bán được số kg đường là:

120−30−40=50120−30−40=50 (kg)

Vậy Ngày thứ 3 bán đc 50kg

a) x + 2/5 = -4/3

x = -4/3 - 2/5

x = -26/15

b) -5/6 + 1/3 x = (-1/2)²

-5/6 + 1/3 x = 1/4

1/3 x = 1/4 + 5/6

1/3 x = 13/12

x = 13/12 : 1/3

x = 13/4

c) 7/12 - (x + 7/6) . 6/5 = (-1/2)³

7/12 - (x + 7/6) . 6/5 = -1/8

(x + 7/6) . 6/5 = 7/12 + 1/8

(x + 7/6) . 6/5 = 17/24

x + 7/6 = 17/24 : 6/5

x + 7/6 = 85/144

x = 85/144 - 7/6

x = -83/144

\(a,x+\dfrac{2}{5}=-\dfrac{4}{3}\\ \Rightarrow x=-\dfrac{26}{15}\\ b,-\dfrac{5}{6}+\dfrac{1}{3}x=\left(-\dfrac{1}{2}\right)^2\\ \Rightarrow-\dfrac{5}{6}+\dfrac{1}{3}x=\dfrac{1}{4}\\ \Rightarrow\dfrac{1}{3}x=\dfrac{13}{12}\\ \Rightarrow x=\dfrac{13}{4}\\ c,\dfrac{7}{12}-\left(x+\dfrac{7}{6}\right).\dfrac{6}{5}=\left(-\dfrac{1}{2}\right)^3\\ \Rightarrow\dfrac{7}{12}-\left(x+\dfrac{7}{6}\right).\dfrac{6}{5}=-\dfrac{1}{8}\\ \Rightarrow\left(x+\dfrac{7}{6}\right).\dfrac{6}{5}=\dfrac{17}{24}\\ \Rightarrow x+\dfrac{7}{6}=\dfrac{85}{144}\\ \Rightarrow x=-\dfrac{83}{144}.\)

a) \(\dfrac{4}{9}+\dfrac{1}{4}=\dfrac{25}{36}\)

b) \(\dfrac{1}{3}\cdot\left(-\dfrac{4}{5}\right)+\dfrac{1}{3}\cdot\left(-\dfrac{1}{5}\right)=\dfrac{1}{3}\cdot\left(-\dfrac{4}{5}-\dfrac{1}{5}\right)=\dfrac{1}{3}\cdot-1=-\dfrac{1}{3}\)

c) \(\dfrac{1}{5}-\left[\dfrac{1}{4}-\left(1-\dfrac{1}{2}\right)^2\right]=\dfrac{1}{5}-\left[\dfrac{1}{4}-\left(\dfrac{1}{2}\right)^2\right]=\dfrac{1}{5}-\left(\dfrac{1}{4}-\dfrac{1}{4}\right)=\dfrac{1}{5}-0=\dfrac{1}{5}\)

`#3107.101107`

`a)`

\(\dfrac{4}{9}+\dfrac{1}{4}=\dfrac{16}{36}+\dfrac{9}{36}=\dfrac{25}{36}\)

`b)`

\(\dfrac{1}{3}\cdot\left(\dfrac{-4}{5}\right)+\dfrac{1}{3}\cdot\left(-\dfrac{1}{5}\right)\)

\(=\dfrac{1}{3}\cdot\left(-\dfrac{4}{5}-\dfrac{1}{5}\right)\)

\(=\dfrac{1}{3}\cdot\left(-1\right)\)

\(=-\dfrac{1}{3}\)

`c)`

\(\dfrac{1}{5}-\left[\dfrac{1}{4}-\left(1-\dfrac{1}{2}\right)^2\right]\)

\(=\dfrac{1}{5}-\left(\dfrac{1}{4}-\dfrac{1}{4}\right)\)

\(=\dfrac{1}{5}-0\)

\(=\dfrac{1}{5}\)

Ta thấy: \(3\left|x+y\right|\ge0\forall x;y\)

              \(10\left|y+\dfrac{2}{3}\right|\ge0\forall y\)

\(\Rightarrow3\left|x+y\right|+10\left|y+\dfrac{2}{3}\right|\ge0\forall x;y\)

Mà: \(3\left|x+y\right|+10\left|y+\dfrac{2}{3}\right|\le0\)

nên: \(\left\{{}\begin{matrix}x+y=0\\y+\dfrac{2}{3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-y\\y=-\dfrac{2}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=-\dfrac{2}{3}\end{matrix}\right.\)

Vậy \(x=\dfrac{2}{3};y=-\dfrac{2}{3}\).

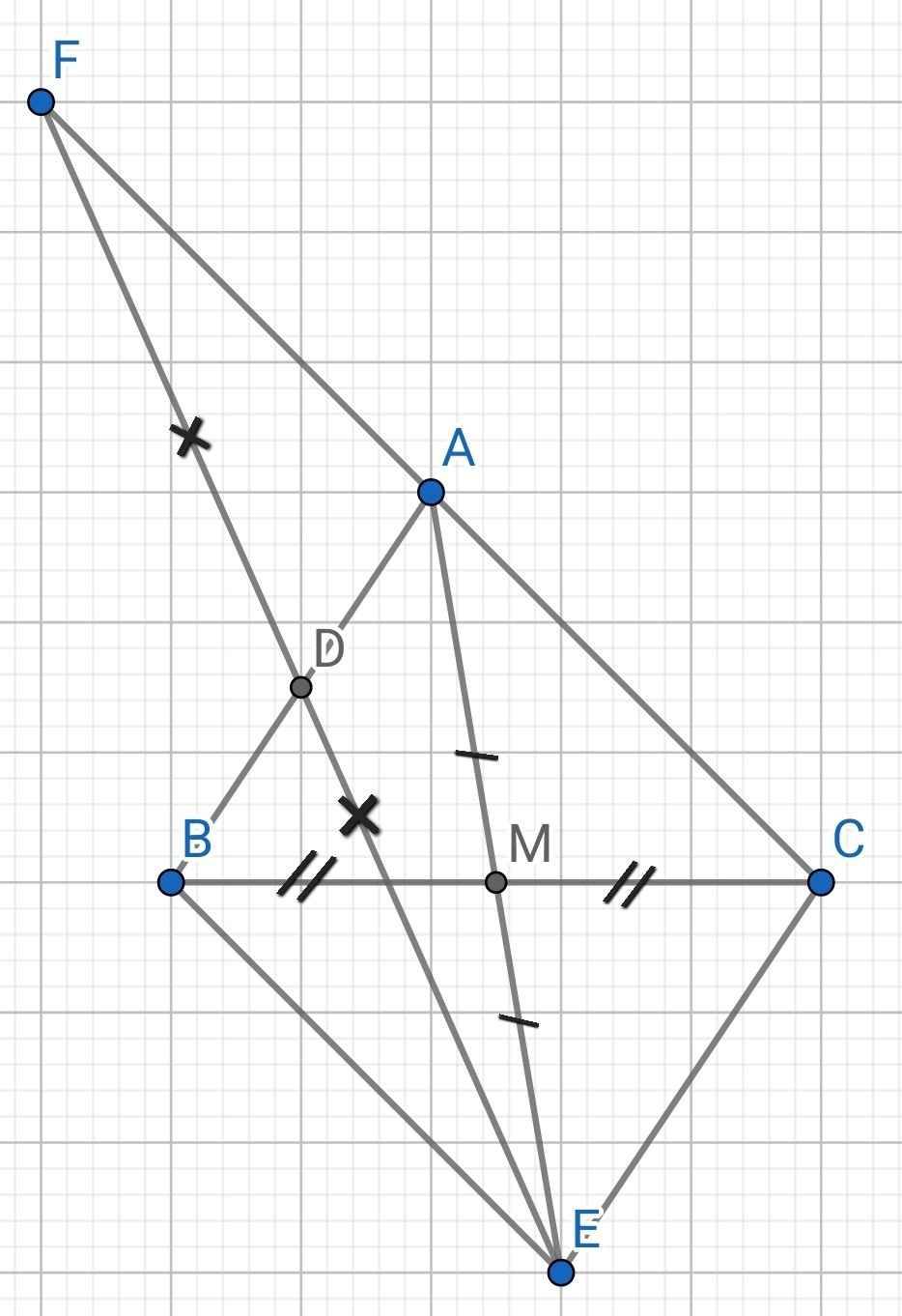 a) Xét ∆AMC và ∆EMB có:

AM = EM (gt)

MC = MB (gt)

∠AMC = ∠EMB (đối đỉnh)

⇒ ∆AMC = ∆EMB (c-g-c)

⇒ AC = BE (hai cạnh tương ứng)

b) Do D là trung điểm AB (gt)

⇒ AD = BD

Xét ∆ADF và ∆BDE có:

AD = BD (cmt)

FD = DE (gt)

∠ADF = ∠BDE (đối đỉnh)

⇒ ∆ADF = ∆BDE (c-g-c)

⇒ AF = BE (hai cạnh tương ứng)

Mà BE = AC (cmt)

⇒ AC = AF

25²⁵ + 5⁴⁹ - 125¹⁶

= (5²)²⁵ + 5⁴⁹ - (5³)¹⁶

= 5⁵⁰ + 5⁴⁹ - 5⁴⁸

= 5⁴⁸.(5² + 5 - 1)

= 5⁴⁸.24

10³ + 2¹⁵

= 1000 + 32768

= 33768

Mà 33768 : 33 = 1023 (dư 9)

Em xem lại đề

a) (-35,8) . (-72,5) - (-33,2) . 72,5

= 72,5.(35,8 + 33,2)

= 72,5 . 69

= 5002,5

b) 2/9 - 1/9 : (1/4 - 1/3)²

= 2/9 - 1/9 : (-1/12)²

= 2/9 - 1/9 : 1/144

= 2/9 - 1/9 . 144

= 2/9 - 144/9

= -142/9

em Hãy tính xem Khởi nghĩa Hai Bà Trưng năm 40 cách năm 2023 là bao nhiêu năm thuộc thế kỷ nào thien niên kỉ ao nhiêu