Cho tam giác ABC nhọn, nội tiếp (O), đường cao BE, CF, trực tâm H. BE cắt (O) tại K.
a) Chứng minh: AH=AK.
b) Chứng minh: AO vuông góc vớiEF.
c) Khi BC cố định, A di chuyển trên (O), chứng minh: đường thẳng qua H vuông góc với EF đi qua một điểm cố định.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(56=2^3\cdot7\\ 84=2^2\cdot3\cdot7\\ 120=2^3\cdot5\cdot3\\=>ƯCLN\left(56;84;120\right)=2^2=4\)

\(2^{x+2}+2^{x+2}+2^{x+1}=224\\ =>2^{x+1}\cdot2+2^{x+1}\cdot2+2^{x+1}\cdot1=224\\ =>2^{x+1}\cdot\left(2+2+1\right)=224\\ =>2^{x+1}\cdot5=224\\ =>2^{x+1}=\dfrac{224}{5}\\ =>x+1=log_2\dfrac{224}{5}\\ =>x=log_2\dfrac{224}{5}-1\)

\(1,x^2+9-16y^2+6x\\ =\left(x^2+6x+9\right)-\left(4y\right)^2\\ =\left(x+3\right)^2-\left(4y\right)^2\\ =\left(x-4y+3\right)\left(x+4y+3\right)\\ 2,x^2-9+y^2+2xy\\ =\left(x^2+2xy+y^2\right)-9\\ =\left(x+y\right)^2-3^2\\ =\left(x+y-3\right)\left(x+y+3\right)\\ 3,x^2-4x+4-9y^2\\ =\left(x-2\right)^2-\left(3y\right)^2\\ =\left(x-3y-2\right)\left(x+3y-2\right)\\ 4,x^2-4xy+4y^2-81\\ =\left(x-2y\right)^2-9^2\\ =\left(x-2y-9\right)\left(x-2y+9\right)\\ 5,6x^2+6y^2-24+12xy\\ =\left(6x^2+12xy+6y^2\right)-24\\ =6\left[\left(x^2+2xy+y^2\right)-4\right]\\ =6\left[\left(x+y\right)^2-2^2\right]\\ =6\left(x+y-2\right)\left(x+y+2\right)\\ 6,9x^2-6x+1-25\\ =\left(3x-1\right)^2-5^2\\ =\left(3x-1-5\right)\left(3x-1+5\right)\\ =\left(3x-6\right)\left(3x+4\right)\)
7: \(x^2+4x+4-49y^2\)
\(=\left(x^2+4x+4\right)-49y^2\)
\(=\left(x+2\right)^2-49y^2\)
=(x+2+7y)(x+2-7y)
8: \(a^3+9a-ab^2-6a^2\)
\(=a\left(a^2-6a+9-b^2\right)\)
\(=a\left[\left(a-3\right)^2-b^2\right]\)
\(=a\left(a-3-b\right)\left(a-3+b\right)\)
9: \(8x^2-16x+8-32y^2\)
\(=8\left(x^2-2x+1-4y^2\right)\)
\(=8\left[\left(x-1\right)^2-\left(2y\right)^2\right]\)
=8(x-1-2y)(x-1+2y)
10: \(4x^2-4x+1-81a^2\)
\(=\left(4x^2-4x+1\right)-81a^2\)
\(=\left(2x-1\right)^2-\left(9a\right)^2\)
=(2x-1-9a)(2x-1+9a)
11: \(x^2-6xy+9y^2-121\)
\(=\left(x^2-6xy+9y^2\right)-121\)
\(=\left(x-3y\right)^2-11^2=\left(x-3y-11\right)\left(x-3y+11\right)\)
12: \(12x^2-24x+12-3y^2\)
\(=3\left(4x^2-8x+4-y^2\right)\)
\(=3\left[\left(2x-2\right)^2-y^2\right]=3\left(2x-2-y\right)\left(2x-2+y\right)\)

\(P=\dfrac{\left(x-1\right)^2+3}{\left(x-1\right)^2+5}=\dfrac{\left(x-1\right)^2+5-2}{\left(x-1\right)^2+5}=1-\dfrac{2}{\left(x-1\right)^2+5}\)
\(\left(x-1\right)^2+5>=5\forall x\)
=>\(\dfrac{2}{\left(x-1\right)^2+5}< =\dfrac{2}{5}\forall x\)
=>\(-\dfrac{2}{\left(x-1\right)^2+5}>=-\dfrac{2}{5}\forall x\)
=>\(P=\dfrac{-2}{\left(x-1\right)^2+5}+1>=-\dfrac{2}{5}+1=\dfrac{3}{5}\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1
\(Q=\dfrac{\left(2y+3\right)^2-3}{\left(2y+3\right)^2+4}=\dfrac{\left(2y+3\right)^2+4-7}{\left(2y+3\right)^2+4}=1-\dfrac{7}{\left(2y+3\right)^2+4}\)
\(\left(2y+3\right)^2+4>=4\forall y\)
=>\(\dfrac{7}{\left(2y+3\right)^2+4}< =\dfrac{7}{4}\forall y\)
=>\(-\dfrac{7}{\left(2y+3\right)^2+4}>=-\dfrac{7}{4}\forall y\)
=>\(Q=-\dfrac{7}{\left(2y+3\right)^2+4}+1>=-\dfrac{3}{4}\forall y\)
Dấu '=' xảy ra khi 2y+3=0
=>2y=-3
=>y=-3/2
\(F=\dfrac{\left(x-1\right)^2+5}{\left(x-1\right)^2+2}=\dfrac{\left(x-1\right)^2+2+3}{\left(x-1\right)^2+2}=1+\dfrac{3}{\left(x-1\right)^2+2}\)
\(\left(x-1\right)^2+2>=2\forall x\)
=>\(\dfrac{3}{\left(x-1\right)^2+2}< =\dfrac{3}{2}\forall x\)
=>\(F=\dfrac{3}{\left(x-1\right)^2+2}+1< =\dfrac{5}{2}\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1

\(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{x\left(x+1\right)}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{x}-\dfrac{1}{x+1}\\ =1+\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3}\right)+...+\left(\dfrac{1}{x}-\dfrac{1}{x}\right)-\dfrac{1}{x+1}\\ =1-\dfrac{1}{x+1}\\ =\dfrac{x+1}{x+1}-\dfrac{1}{x+1}\\ =\dfrac{x}{x+1}\)

\(5^{2x-1}=125\\ =>5^{2x-1}=5^3\\ =>2x-1=3\\ =>2x=3+1\\ =>2x=4\\ =>x=\dfrac{4}{2}\\ =>x=2\)
Vậy: ...
52x - 1 = 125
52x - 1 = 53
2x - 1 = 3
2x = 3 +1
2x = 4
x = 4 :2
x = 2

a, 19 + 18 + 17 + 16 + 14 + 21 + 22 + 23 + 24 + 26
= ( 19 + 21 ) + ( 18 + 22 ) + ( 17 + 23 ) + ( 16 + 24 ) + ( 14 + 26 )
= 40 + 40 + 40 + 40 + 40
= 40 x 5
= 200
Chúc bé học tốt
a.
19 + 18 + 17 + 16 + 14 + 21 + 22 + 23 + 24 + 26
= (19 + 21) + (18 + 22) + (17 + 23) + ( 16 + 24) + (14 + 26)
= 40 + 40 + 40 + 40 + 40
= 40 x 5
= 200
câu b mk đã lm ở dưới r nhé
c) 64 x 4 + 18 x 4 + 9 x 8
= 64 x 4 + 18 x 4 + 9 x 2 x 4
= 4 x ( 64 + 18 + 9 x 2)
=4 x (82 + 18)
= 4 x 100
= 400

\(15,2-x+12=93\)
\(15,2-x=93-12\)
\(15,2-x=81\)
\(x=15,2-81\)
\(x=-65,8\)
Em có nhầm ko nhỉ, lớp 4 sao đã có số âm được
lớp 4 chưa học số thập phân và số âm, hình như em viết sai đề bài.
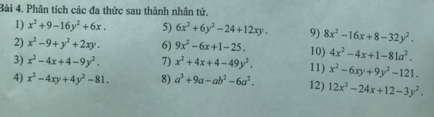
a:Xét ΔABC có
BE,CF là các đường cao
BE cắt CF tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại D
Xét (O) có \(\widehat{AKB};\widehat{ACB}\) là các góc nội tiếp chắn cung AB
nên \(\widehat{AKB}=\widehat{ACB}\)
mà \(\widehat{ACB}=\widehat{AHE}\left(=90^0-\widehat{DAC}\right)\)
nên \(\widehat{AKB}=\widehat{AHE}\)
=>\(\widehat{AHK}=\widehat{AKH}\)
=>AK=AH
b: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>\(\widehat{FEC}+\widehat{FBC}=180^0\)
mà \(\widehat{CEF}+\widehat{AEF}=180^0\)
nên \(\widehat{AEF}=\widehat{ABC}\)
Gọi Ax là tiếp tuyến tại A của (O)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
DO đó: \(\widehat{xAC}=\widehat{ABC}\)
=>\(\widehat{xAC}=\widehat{AEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên FE//Ax
mà Ax\(\perp\)OA
nên OA\(\perp\)EF