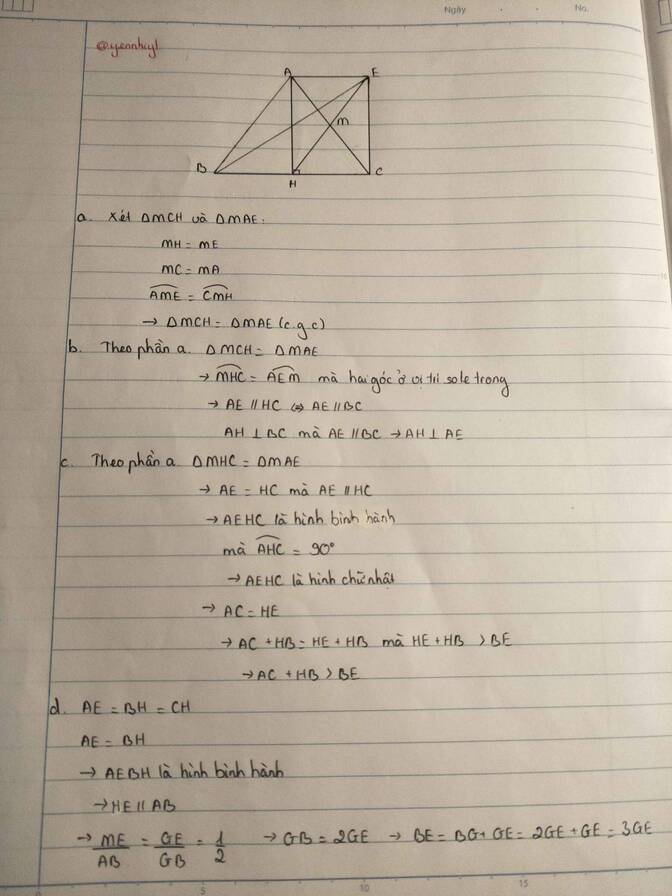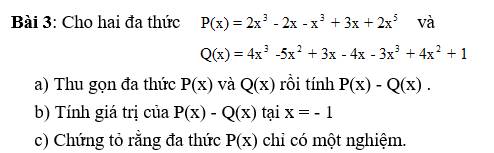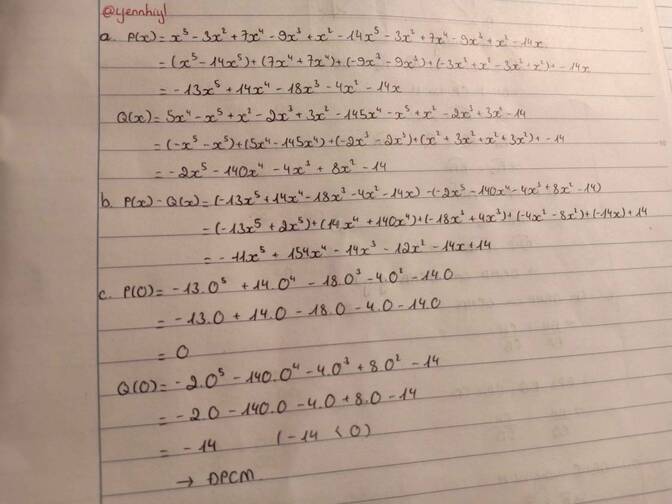Cho tam giác ABC cân tại A, có H và M thứ tự là trung điểm của BC và AC. Trên tia đối của
tia MH lấy điểm E sao cho ME = MH :
a) Chứng minh: tam giác MCH= tam giác MAE
b) Chứng minh: AE // BC, AH vuông góc AE
c] Chứng minh: AC+HB>BE
d] Gọi giao điểm của BE với AC là G. Chứng minh BE=3GE