Tìm nghiệm đa thức:
K(x)=(x+3)^2+(x^2-9)^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


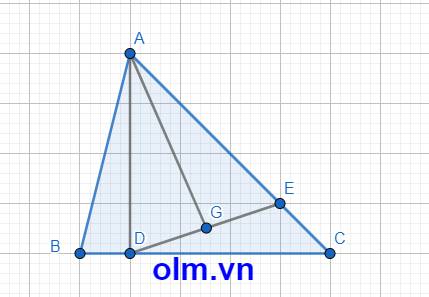
SADE = 2\(\times\)SAGE ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DE và DE = 2\(\times\) GE )
⇒ SADE = 36 \(\times\) 2 = 72 (cm2)
SADE = \(\dfrac{3}{4}\)\(\times\)SADC (vì hai tam giác có chung chiều cao hạ từ Đỉnh D xuống đáy AC và AE = \(\dfrac{3}{4}\)AC)
⇒ SACD = 72 : \(\dfrac{3}{4}\) = 96 (cm2)
DC = BC - BD = BC - \(\dfrac{1}{5}\)BC = \(\dfrac{4}{5}\)BC
SADC = \(\dfrac{4}{5}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và DC = \(\dfrac{4}{5}\)BC)
⇒ SABC = 96 : \(\dfrac{4}{5}\) = 120 (cm2)
Tỉ số phần trăm diện tích tam giác ADE và diện tích tam giác ABC là:
72 : 120 = 0,6
0,6 = 60%
Đáp số: 60%

2 lần hiệu tuổi Nam và tuổi em của Nam là:
30 - 24 = 6 ( tuổi )
Hiệu số tuổi của Nam và em Nam là :
6 : 2 = 3 ( tuổi )
Hiệu số tuổi của bố và mẹ là :
3 x 3 = 9 ( tuổi )
Tổng số tuổi của bố và mẹ là :
( 92 + 30 + 24 ) : 2 = 73 ( tuổi )
Số tuổi của bố là :
( 73 + 9 ) : 2 = 41 ( tuổi )
Số tuổi của mẹ là :
73 - 41 = 32 ( tuổi )
Bố hơn mẹ số tuổi là:
41 - 32 = 9 tuổi
Đây là dạng toán nâng cao hiệu tỉ, ẩn hiệu của tiểu học em nhé. Hôm nay olm.vn sẽ hướng dẫn em giải dạng này như sau:Bước 1 tìm hiệu đang bị ẩn. Bước 2: giải toán hiệu tỉ bình thường
Hiệu của tuổi bố và tuổi mẹ hơn hiệu của tuổi Nam và tuổi em Nam là:
30 - 24 = 6 (tuổi)
Ta có sơ đồ:

Theo sơ đồ ta có: Hiệu của tuổi bố và tuổi mẹ là: 6:(3-1)\(\times\)3 = 9 (tuổi)
Vậy bố hơn mẹ 9 tuổi
Đáp số: 9 tuổi

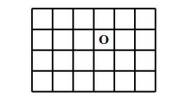
Coi cạnh của hình vuông là 1 đơn vị
Số hình vuông có kích thước 1:1 và chứa chữ O là: 1 hình
Số hình vuông có kích thước 2:2 có chứa chữ O là 4 hình
Số hình vuông có kích thước 3:3 có chứa chữ O là 4 hình
Số hình vuông có kích thước 4:4 có chứa chữ O là 6 hình
Có tất cả số hình vuông có chứa chữ O là:
1+ 4 + 4 + 6 = 15 (hình)
Đáp số: 15 hình
mình nghĩ là làm cách này cơ
bài làm
Hình vuông với kích thước 1 x 1 có chứa chữ O là: 1 hình
Hình vuông với kích thước 2 x 2 có chứa chữ O là: 4 hình
Hình vuông với kích thước 3 x 3 có chứa chữ O là: 6 hình
Hình vuông với kích thước 4 x 4 có chứa chữ O là: 3 hình
Vậy tổng số hình vuông có chứa chữ O là: 1 + 4 + 6 + 3 = 14 (hình)

Gọi hai số tự nhiên thỏa mãn đề bài theo thứ tự từ bé đến lớn lần lượt là:
b ; a 300 ≤ b < a ≤ 400;
Ta có: a - b = 84 và ƯCLN(a,b) = 84
⇒ \(\left\{{}\begin{matrix}a=28\times c\\b=28\times d\end{matrix}\right.\) (c; d) = 1
28 \(\times\) c - 28 \(\times\) d = 84
28\(\times\)(c-d) = 84
c - d = 3 ⇒ d = c - 3
Mặt khác ta cũng có: 300 ≤ a ≤ 400 ⇒ 300 ≤ 28 \(\times\) c ≤ 400
⇒\(\dfrac{75}{7}\) ≤ c ≤ \(\dfrac{100}{7}\) ⇒ 10,7 ≤ c ≤ 14,2 vì c \(\in\) N nên c = 11; 12; 13
lập bảng ta có:
| c | 11 | 12 | 13 |
| d = c - 3 | 8 | 9 (loại) | 10 |
| a = 28 \(\times\) c | 308 | 364 | |
| b = 28 \(\times\) d | 224 | 280 |
Theo bảng trên ta có hai cặp số tự nhiên thỏa mãn đề bài là:
(224; 308) và (280; 364)

Cách 1: Quãng đường mà hình tròn A lăn được bằng quãng đường di chuyển của tâm hình tròn A. Tâm I của hình tròn A cách tâm hình tròn B một khoảng bằng 4 lần bán kính của hình tròn A (tương ứng, chu vi của đường tròn mà I vạch nên cũng gấp 4 lần chu vi hình A). Vì vậy, hình A phải thực hiện 4 vòng quay mới trở lại điểm xuất phát.
Cách 2: Dễ thấy chu vi hình B gấp 3 lần chu vi hình A. Chia đường tròn lớn thành 3 phần bằng nhau bởi 3 điểm M, N, P (hình vẽ), mỗi phần như vậy có độ dài bằng chu vi hình A. Khi hình A lăn từ M đến N theo chiều kim đồng hồ, bán kính nối tâm hình tròn A với điểm tiếp xúc giữa 2 hình tròn (bán kính màu đen) quét một góc 3600+1200. Tương tự cho 2 phần còn lại, để hình A trở về điểm xuất phát thì bán kính màu đen quét 1 góc tổng cộng là: 3 x ( 3600 + 1200 ) = 4 x 3600, tức 4 vòng quay.

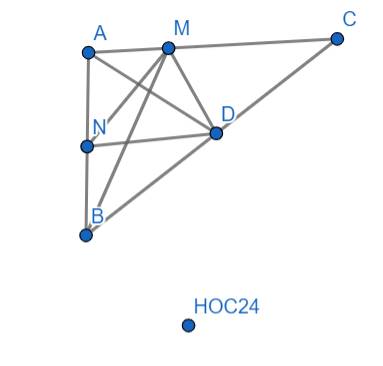
Ta có:
\(S_{ADM}=\dfrac{1}{2}\cdot AM\cdot h\)
\(S_{ADC}=\dfrac{1}{2}\cdot AD\cdot h\)
Mà: \(AM=\dfrac{1}{3}AC\Rightarrow AC=3AM\)
Ta lại có:
\(S_{ADC}=\dfrac{1}{2}\cdot DC\cdot h\)
\(S_{ABC}=\dfrac{1}{2}\cdot BC\cdot h\)
Mà: \(DC=\dfrac{1}{2}BC\Rightarrow BC=2DC\)
\(\Rightarrow S_{ABC}=2S_{ADC}=2\cdot3S_{ADM}=6S_{ADM}\)
b) Chứng minh tiếp tục câu a) ta sẽ có được:
\(S_{AMN}=\dfrac{1}{6}S_{ABC}\)
\(S_{CMD}=\dfrac{1}{3}S_{ABC}\)
\(S_{BND}=\dfrac{1}{4}S_{ABC}\)
\(\Rightarrow S_{DMN}=\left(1-\dfrac{1}{6}-\dfrac{1}{3}-\dfrac{1}{4}\right)S_{ABC}=\dfrac{1}{4}S_{ABC}=\dfrac{1}{4}\cdot600=150cm^2\)

1. Giá trị của biểu thức là:
\(15:1,5+2,5\times0,2=10+0,5=10,5\)
2. Thể tích nước cần đổ:
\(\dfrac{1}{2}\times2=1\left(m^3\right)\)
Số lít nước cần đổ:
\(1\left(m^3\right)=1000\left(dm^3\right)=1000l\)
3. \(0,1356+5\times0,1356-0,1356\times6\)
\(=0,1356\times\left(1+5-6\right)\)
\(=0,1356\times0\)
\(=0\)
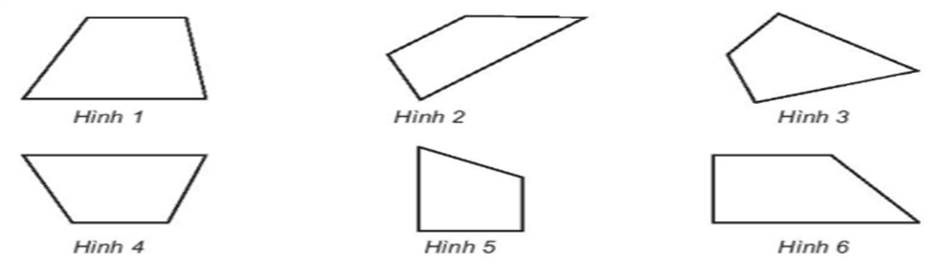
4. Các hình thang là: hình 1, hình 4, hình 5, hình 6

1 tuẫn lễ = 7 ngày
Tuần thứ 2 dùng hết số lít là: 182,45+27,1=209,55(lít)
Cả hai tuần dùng số lít là: 182,45+209,55=392(lít)
Trung bình cả hai tuần 1 ngày dùng số lít là: 392:7=56(lít)
Đ/S:...
Chúc bạn học tốt, tích cho mình nhé
Tuần thứ hai nhà hàng dùng hết số dầu ăn là:
182,45 + 27,1 = 209,55 (l)
Cả hai tuần nhà hàng đã dùng hết số dầu ăn là:
209,55 + 182,45 = 392 (l)
Một tuần = 7 ngày
392 l dầu ăn nhà hàng đã dùng hết trong số ngày là:
7 \(\times\) 2 = 14 (ngày)
Trung bình mỗi ngày trong hai tuần lễ đó nhà hàng dùng hết số lít dầu ăn là:
392 : 14 = 28 (l)
Đáp số: 28 (l)

Diện tích hồ cá:
\(5\times5\times3,14=78,5\left(m^2\right)\)
Bán kính của cả con đường và hồ cá:
\(5+2=7\left(m\right)\)
Diện tích của cả con đường và hồ cá:
\(7\times7\times3,14=153,86\left(m^2\right)\)
Diện tích con đường:
\(153,86-78,5=\text{ }75,36\left(m^2\right)\)

Cho \(K\left(x\right)=0\)
\(=>\left(x+3\right)^2+\left(x^2-9\right)^2=0\\ =>\left\{{}\begin{matrix}x+3=0\\x^2-9=0\end{matrix}\right.\\ =>\left\{{}\begin{matrix}x=-3\\x^2=9\end{matrix}\right.\\ =>\left\{{}\begin{matrix}x=-3\\x=\pm3\end{matrix}\right.=>x=-3\)
Vậy `x=-3` là nghiệm đa thức
cho mình hỏi vì sao x=-3, x=+-3 lại => là x=-3 vậy?