Áp dụng BĐT Bunhiacopxki:

\(\sqrt{\left(a^2+c^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ac+bc\right)^2}=ac+bc\)

CMTT : \(\sqrt{\left(a^2+d^2\right)\left(b^2+d^2\right)}\ge ad+bd\)

Ta có :\(\sqrt{\left(a^2+c^2\right)\left(b^2+c^2\right)}+\sqrt{\left(a^2+d^2\right)\left(b^2+d^2\right)}\ge ac+bc+ad+bd=\left(a+b\right)\left(c+d\right)\)

Áp dụng BĐT Bunhiacopxki:

$\sqrt{\left(a^2+c^2\right)\left(b^2+c^2\right)}\ge \sqrt{{\left(ac+bc\right)}^2}=ac+bc$

CMTT : $\sqrt{\left(a^2+d^2\right)\left(b^2+d^2\right)}\ge ad+bd$

Ta có :$\sqrt{\left(a^2+c^2\right)\left(b^2+c^2\right)}+\sqrt{\left(a^2+d^2\right)\left(b^2+d^2\right)}\ge ac+bc+ad+bd=\left(a+b\right)\left(c+d\right)$

=..

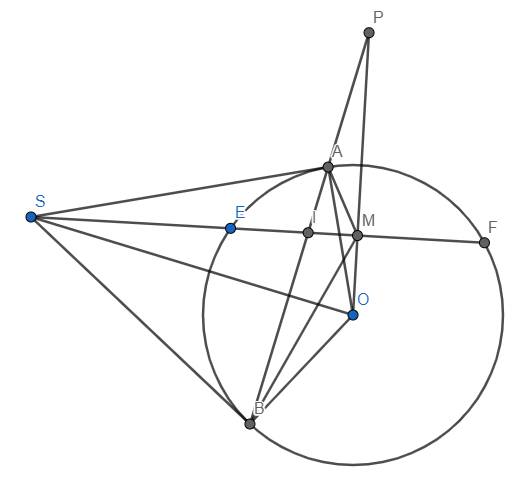
a) Do SA là tiếp tuyến tại A của (O) nên \(\widehat{OAS}=90^o\). Tương tự, ta có \(\widehat{OBS}=90^o\), suy ra \(\widehat{OAS}+\widehat{OBS}=180^o\). Do đó tứ giác SAOB nội tiếp. (đpcm)

 Mặt khác, trong đường tròn (O) có M là trung điểm của dây EF nên \(OM\perp EF\) tại M hay \(\widehat{OMS}=90^o\). Từ đó suy ra \(\widehat{OMS}=\widehat{OAS}\),từ đó tứ giác OMAS nội tiếp. Vì vậy 5 điểm O, M, A, S, B cùng thuộc một đường tròn \(\Rightarrow\) Tứ giác SAMO nội tiếp (đpcm)

b) Ta thấy tứ giác OMAB nội tiếp nên \(\widehat{PMA}=\widehat{PBO}\). Từ đó dễ dàng suy ra \(\Delta PAM~\Delta POB\left(g.g\right)\Rightarrow\dfrac{PA}{PO}=\dfrac{PM}{PB}\) \(\Rightarrow PA.PB=PO.PM\) (đpcm)

c) Do tứ giác SAMB nội tiếp nên \(\widehat{SMB}=\widehat{SAB}\) và \(\widehat{SMA}=\widehat{SBA}\). Mặt khác, trong đường tròn (O), có 2 tiếp tuyến tại A và B cắt nhau tại S nên \(SA=SB\) hay \(\Delta SAB\) cân tại S \(\Rightarrow\widehat{SAB}=\widehat{SBA}\) \(\Rightarrow\widehat{SMB}=\widehat{SMA}\) hay MI là phân giác trong của \(\widehat{AMB}\) . Lại có \(MP\perp MI\) nên MP là phân giác ngoài của \(\widehat{AMB}\). Áp dụng tính chất đường phân giác, ta thu được \(\dfrac{IA}{IB}=\dfrac{MA}{MB}\) và \(\dfrac{PA}{PB}=\dfrac{MA}{MB}\). Từ đây suy ra \(\dfrac{IA}{IB}=\dfrac{PA}{PB}\) \(\Rightarrow PA.IB=PB.IA\) (đpcm)

Bài làm :

1. Trường hợp 1 :

F₁ có tỉ lệ phân li 3 quả đỏ : 1 quả vàng . Quả vàng có kiểu gen aaa chứng tỏ những cây P đem lại ở đây ít nhất có 2 gen lặn aa. Mặt khác , với 3+1=4 tổ hợp là kết quả thụ phấn giữa 2 loại giao tử cái . Để cho ra 2 loại giao tử với tỉ lệ ngang nhau trong đó có giao tử mang aa thì kiểu gen của cây P là Aaaa.

Sơ đồ lai :

P:             Quả đỏ                  .               Quả đỏ

                 Aaaa                                      Aaaa

G_P:            (1Aa : 1aa)                          (1Aa : 1aa )

F₁ : 1/4 AAaa : 2/4 Aaaa            :               1/4 aaaa

               3 quả đỏ                                              1 quả vàng

2. Trường hợp 2 :

F₁ có tỉ lệ phân li 11 quả đỏ : 1 quả vàng , trong đó cây quả vàng có kiểu gen aaaa , do đó ở cây P có ít nhất 2 gen a . Mặt khác với 11+1=12 tổ hợp có thể giải thích là một bên P cho ra 3 loại giao tử với tỉ lệ 1:4:1 , còn một bên cho 2 loại giao tử với tỉ lệ 1:1 . Từ đó suy ra : một bên P có kiểu gen AAaa còn bên P còn lại có kiểu gen Aaaa

Sơ đồ lai :

P :                  Quả đỏ                .            Quả đỏ 

                 AAaa                                               Aaaa

G_P:           ( 1AA:4Aa:1aa)                             ( 1Aa:1aa)

F₁:           1AAAa:5AAaa:5Aaaa          :                1aaaa

                    11 quả đỏ                                              1 quả vàng