Tính tổng S=1.2.3+2.3.5+...+n(n+1)(2n+1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(7,\) \(a,\left(2x-3y\right)^2-\left(2x+3y\right)^2=\left(3x-2y\right)^2-\left(3x+2y\right)^2\)
\(\Leftrightarrow4x^2-12xy+9y^2-4x^2-12xy-9y^2=9x^2-12xy+4y^2-9x^2-12xy-4y^2\)
\(\Leftrightarrow-24xy=-24xy\) ( luôn đúng )
Vậy 2 đẳng thức ở 2 vế bằng nhau.
\(b,\left(a^2+b^2\right)\left(c^2+d^2\right)=\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(\Leftrightarrow\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2=\left(ac\right)^2+2acbd+\left(bd\right)^2+\left(ad\right)^2-2adbc+\left(bc\right)^2\)
\(\Leftrightarrow\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2=\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2\) ( luôn đúng )
Vậy 2 đẳng thức ở 2 vế bằng nhau.
*Ở câu \(b,\) dòng thứ 3, vế phải triệt tiêu \(2acbd-2adbc\) \(=0\) nên mất rồi nha.

`@` `\text {Ans}`
`\downarrow`
`8,`
`a,`
Thay \(x=18;y=41\) vào bt
\(18^2-4\cdot41^2\)
`= 18^2 - (2*41)^2`
`= 18^2 - 82^2`
`= -6400`
`b,`
\(87^2+13^2+26\cdot87\)
`= 87*(87+26) + 169`
`= 87*113 + 169`
`= 9831 + 169`
`= 10000`
\(9,\) \(a,\left(2x+1\right)^2-4\left(x-1\right)\left(x+1\right)=2x-4\)
\(\Leftrightarrow4x^2+4x+1-4\left(x^2-1\right)-2x+4=0\)
\(\Leftrightarrow4x^2+4x+1-4x^2+4-2x+4=0\)
\(\Leftrightarrow\left(4x^2-4x^2\right)+\left(4x-2x\right)+\left(1+4+4\right)=0\)
\(\Leftrightarrow2x=-9\)
\(\Leftrightarrow x=-\dfrac{9}{2}\)
Vậy \(S=\left\{-\dfrac{9}{2}\right\}\)
\(b,\left(-3+x\right)^2-2\left(2-x\right)\left(x+2\right)-3\left(x+1\right)^2=4\)
\(\Leftrightarrow9-6x+x^2-2\left(2x+4-x^2-2x\right)-3\left(x^2+2x+1\right)-4=0\)
\(\Leftrightarrow9-6x+x^2-4x-8+2x^2+4x-3x^2-6x-3-4=0\)
\(\Leftrightarrow-12x=6\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(S=\left\{-\dfrac{1}{2}\right\}\)
\(c,3x^2+\left(-1-x\right)^2=\left(2x+5\right)\left(2x-5\right)\)
\(\Leftrightarrow3x^2+1+2x+x^2=4x^2-25\)
\(\Leftrightarrow2x=-26\)
\(\Leftrightarrow x=-13\)
Vậy \(S=\left\{-13\right\}\)

Ta có: \(C=\dfrac{bc}{a^2}+\dfrac{ac}{b^2}+\dfrac{ab}{c^2}\)
\(C=\dfrac{abc}{a^3}+\dfrac{abc}{b^3}+\dfrac{abc}{c^3}\)
\(C=abc\left(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}\right)\)
Vì: \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}=-\dfrac{1}{c}\)
\(\Rightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^3=\left(-\dfrac{1}{c}\right)^3\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{3}{ab}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=-\dfrac{1}{c^3}\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}+\dfrac{3}{ab}\left(-\dfrac{1}{c}\right)=0\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}+-\dfrac{3}{abc}=0\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\left(1\right)\)
Thay (1) vào C ta được:
\(C=abc\left(\dfrac{3}{abc}\right)\)
\(\Rightarrow C=3\)

a) \(\left(-x-4\right)^2\)
\(=\left(-x\right)^2-2\cdot\left(-x\right)\cdot4+4^2\)
\(=x^2+8x+16\)
b) \(\left(-5+3x\right)^2\)
\(=\left(-5\right)^2+2\cdot\left(-5\right)\cdot3x+\left(3x\right)^2\)
\(=25-30x+9x^2\)
c) \(\left(-x-3\right)\left(x-3\right)\)
\(=-\left(x+3\right)\left(x-3\right)\)
\(=-\left(x^2-9\right)\)


Cho \(K\left(x\right)=0\)
\(=>\left(x+3\right)^2+\left(x^2-9\right)^2=0\\ =>\left\{{}\begin{matrix}x+3=0\\x^2-9=0\end{matrix}\right.\\ =>\left\{{}\begin{matrix}x=-3\\x^2=9\end{matrix}\right.\\ =>\left\{{}\begin{matrix}x=-3\\x=\pm3\end{matrix}\right.=>x=-3\)
Vậy `x=-3` là nghiệm đa thức

- dotrungminhnhat

- 14/08/2021
Ta có:
A� = `2121 . 4343 . 6565........200199200199`
A� < `2121..3232..5454............199198199198`
⇒⇒ A²�² < `2.4.6...2001.3.5.1992.4.6...2001.3.5.199..2.3.5....1991.2.4....1982.3.5....1991.2.4....198`
== 200.2=400200.2=400
⇒⇒ A<20�<20.
Để chứng minh A > 14, ta làm giảm mỗi phân số của A bằng cách dùng bất đẳng thức:
`n+1n�+1� > n+2n+1�+2�+1`.
Chứng minh tương tự ta có: 14<A14<�
Vậy 14<A<2014<�<20.

`@` `\text {Ans}`
`\downarrow`
\(3(x^2+2x-3)+3(-x^2-4x)\)
`= 3*(x^2+2x-3 - x^2 - 4x)`
`= 3*[(x^2-x^2)+(2x-4x)-3]`
`= 3*(-2x-3)`
`= -6x-9`
3(x² + 2x - 3) + 3(-x² - 4x)
= 3x² + 6x - 9 - 3x² - 12x
= (3x² - 3x²) + (6x - 12x) - 9
= -6x - 9
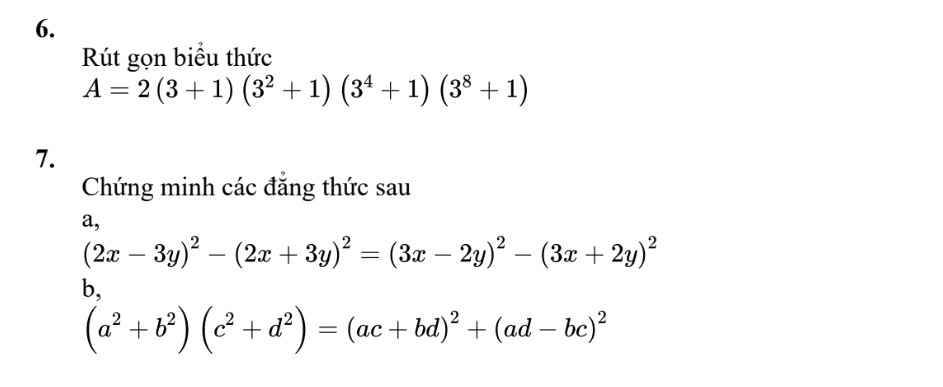
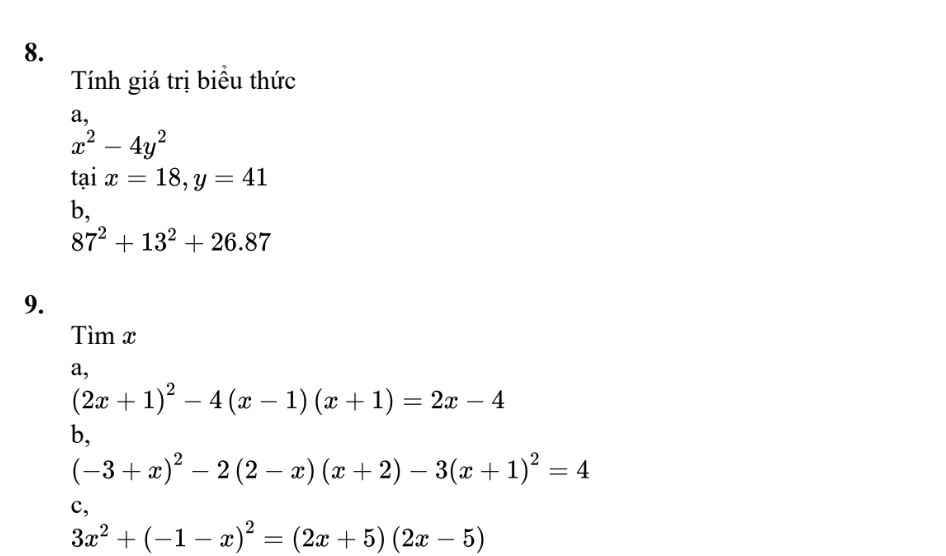
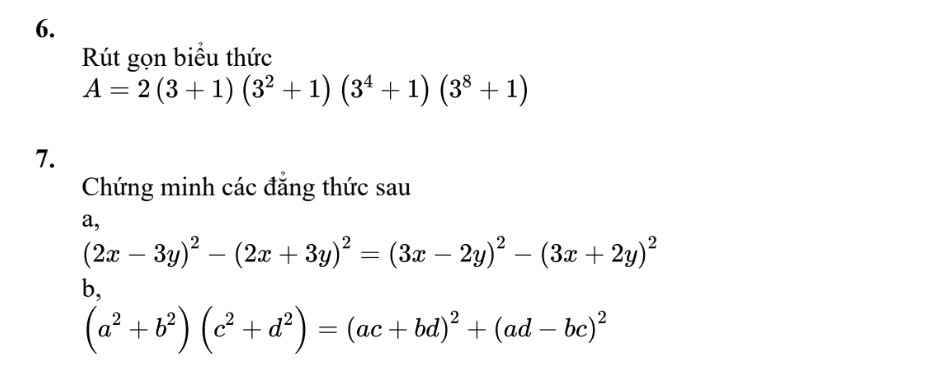
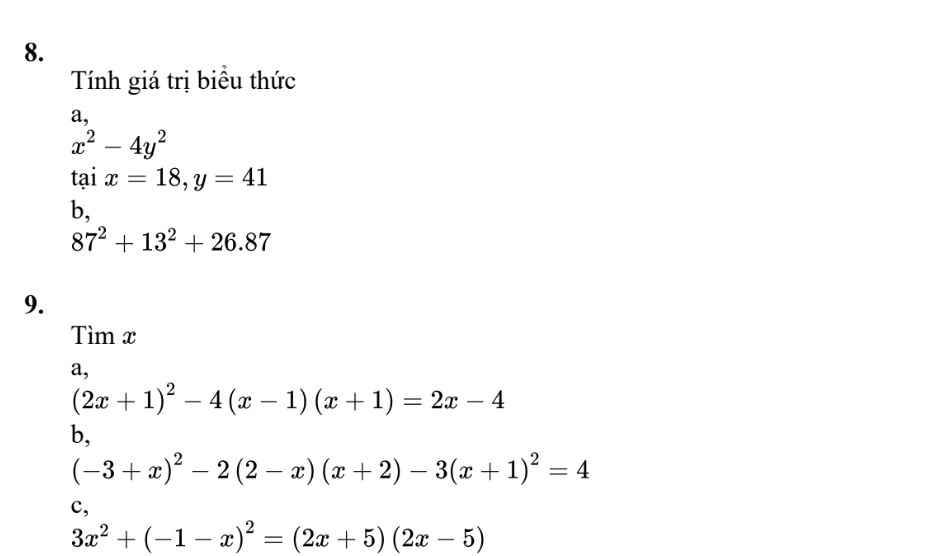

S=1.2.3+2.3.(4+1)+3.4.(5+2)+...+n(n+1)[(n+2).(n-1)=
=1.2.3+1.2.3+2.3.4+2.3.4+3.4.5+...+(n-1)n(n+1)+n(n+1)(n+2)=
=2[1.2.3+2.3.4+3.4.5+...+(n-1)n(n+1)]+n(n+1)(n+2)
Đặt
A=1.2.3+2.3.4+3.4.5+...+(n-1)n(n+1)
4A=1.2.3.4+2.3.4.4+3.4.5.4+...+(n-1)n(n+1).4=
=1.2.3.4+2.3.4.(5-1)+3.4.5.(6-2)+...+(n – 1).n.(n + 1).[(n + 2) – (n – 2)]
=1.2.3.4 + 2.3.4.5 – 1.2.3.4 + 3.4.5.6 – 2.3.4.5 + … + (n – 1).n(n + 1).(n + 2) – (n – 2).(n – 1).n.(n + 1)=
= (n – 1).n(n + 1).(n + 2)
2A=\(\dfrac{\left(n-1\right)n\left(n+1\right)\left(n+2\right)}{2}\)
S=2A+n(n+1)(n+2)