Tính tổng các hệ số của đa thức nhận được sau khi bỏ dấu ngoặc trong biểu thức P(x) = (8x2 + 3x - 10)2018 . (8x2 + x - 10) 2019
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\dfrac{y+z+1}{x}=\dfrac{z+x+2}{y}=\dfrac{x+y-3}{z}=x+y+z\left(1\right)\)
Ta có:
\(\dfrac{y+z+1}{x}=\dfrac{z+x+z}{y}=\dfrac{x+y-3}{z}=\dfrac{y+z+1+z+x+2+x+y-3}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}\left(2\right)\)
Trường hợp 1: \(x+y+z=0\Leftrightarrow x=y=z=0\)
Trường hợp 2: \(x+y+z\ne0\)
\(\left(2\right)\Rightarrow\left\{{}\begin{matrix}y+z+1=2x\\x+z+2=2y\\x+y-3=2z\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y+z=3x-1\\x+y+z=3y-2\\x+y+z=3z+3\end{matrix}\right.\Rightarrow3x-1=3y-2=3z+3\Rightarrow\left\{{}\begin{matrix}x=z+\dfrac{4}{3}\\y=z+\dfrac{5}{3}\end{matrix}\right.\)
\(\left(1\right)\Rightarrow\dfrac{z}{z+\dfrac{4}{3}+z+\dfrac{5}{3}-3}=z+\dfrac{4}{4}+z+\dfrac{5}{4}+z\)
\(\Rightarrow\dfrac{1}{2}=3+3z\)
\(\Rightarrow z=-\dfrac{5}{6}\)
\(\Rightarrow x=-\dfrac{5}{6}+\dfrac{4}{3}=\dfrac{1}{2}\)
\(\Rightarrow y=-\dfrac{5}{6}+\dfrac{5}{3}=\dfrac{5}{6}\)

8<2n<648<2n<64⇔23<2n<26⇔23<2n<26⇔3<n<6⇔3<n<6
Vì n nguyên dương ⇒n∈{4;5}⇒n∈{4;5}
Vậy n∈{4;5}
_HT_



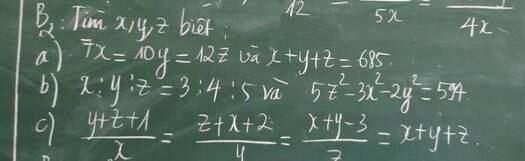 Các bạn giải giúp mình ý c với
Các bạn giải giúp mình ý c với 