Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a,`
`2x^2 - 6x`
`= 2 (x^2 - 3x) `
`= 2 (x^2 - 2 . x . 3/2 + 9/4 - 9/4)`
`= 2 (x-3/2)^2 -9/2 >= 9/2`
Dấu "=" xảy ra khi :
`<=> (x-3/2)^2=0 <=> x-3/2=0 <=> x=3/2`
Vậy GTNN của BT là `9/2 <=> x=3/2`
`b,`
`x^2 + y^2 - x + 6y +10`
`= (x^2 - x)+(y^2 + 6y)+10`
`= (x^2 - 2 . x . 1/2 +1/4) + (y^2 + 2 . y . 3 + 9) +3/4`
`= (x-1/2)^2 + (y+3)^2 + 3/4 >= 3/4`
Dấu "=" xảy ra khi :
`<=> (x-1/2)^2=0, (y+3)^2=0`
`<=> x=1/2, y=-3`
Vậy GTNN của BT là `3/4 <=> x=1/2, y=-3`

a) 3x*(x+2)=0 \(\Leftrightarrow\orbr{\begin{cases}x=0\\x=-2\end{cases}}\)
b) (2x+3)(x-1-2x)=0<=>(2x+3)(-x-1)=0\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{3}{2}\\x=-1\end{cases}}\)
c) (2x+1)2=0<=>x=-1/2
d) x2-4x-3=0<=>\(\orbr{\begin{cases}x=2+\sqrt{7}\\x=2-\sqrt{7}\end{cases}}\)
`a,`
`3x^2 +6x=0 -> 3x (x+2)=0`
TH1 : `3x=0 ->x=0`
TH2 : `x+2=0 ->x=-2`
Vậy `x=0,x=-2`
`b,`
`(2x+3)(x-1)=2x(2x+3) -> (2x+3)(x-1)-2x (2x+3) -> (2x+3)(x-1-2x)=0`
TH1 : `2x+3=0 ->x=(-3)/2`
TH1 : `-x-1=0 ->x=-1`
Vậy `x=(-3)/2, x=-1`
`c,`
`4x^2 +4x+1=0 -> (2x)^2 + 2 . 2x.1+1^2=0 -> (2x+1)^2=0`
`->2x+1=0 ->2x=-1 ->x=(-1)/2`
Vậy `x=(-1)/2`
`d,`
`x^2 - 4x=3 ->x^2 - 4x-3=0 ->x^2 - 2 . x . 2 + 2^2 -7 =0`
`-> (x-2)^2 =7`
TH1 : `x-2=\sqrt{7} ->x=2+\sqrt{7}`
TH2 : `x-2=-\sqrt{7} ->x=2 -\sqrt{7}`
Vậy ..

Ta có C = x3 + y3 = ( x + y ) ( x2 - xy + y2 ) = 3 [ ( x2 + 2xy + y2 ) - 3xy ] = 3 ( x + y )2 - 3.3xy
= 3. 32 - 3.3.2 = 27 - 18 = 9
Có : `(x+y)^3 = x^3 + y^3 + 3xy (x+y)`
`-> x^3 + y^3 = (x+y)^3 - 3xy (x+y)`
`->x^3 + y^3 = 3^3 - 3 . 2 . 3`
`-> x^3 + y^3 = 27 - 18`
`->x^3 + y^3=9`
Vậy `x^3+y^3=9`

\(M=-4x^2+6x-9\)
\(=-\left(4x^2-6x+9\right)=-\left(4x^2-2.2x\frac{3}{2}+\frac{9}{4}+\frac{27}{4}\right)=-\left(2x-\frac{3}{2}\right)^2-\frac{27}{4}\)
Ta có: \(\left(2x-\frac{3}{2}\right)^2\ge0\forall x\Rightarrow-\left(2x-\frac{3}{2}\right)^2\le0\Rightarrow-\left(2x-\frac{3}{2}\right)^2-\frac{27}{4}\le\frac{-27}{4}\)
Dấu '' = '' xảy ra khi: \(2x-\frac{3}{2}=0\Rightarrow x=\frac{3}{4}\)
`M= -4x^2 +6x-9`
`->M = -(4x^2 - 6x +9) =- [(2x)^2 - 2 . 2x . 3/2 + 9/4 +27/4] = -(2x - 3/2)^2 - 27/4 =< (-27)/4`
Dấu "=" xảy ra khi : `<=> (2x-3/2)^2=0 <=>x=3/4`
Vậy `max M=(-27)/4 <=> x=3/4`


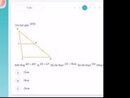
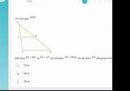


xét tam giác ABD có
[laTEX]\frac{AB}{sin 90} = \frac{AD}{sin 36} \Rightarrow AD = sin 36. AB[/laTEX]
xét tam giác ABE có
[laTEX]\frac{AB}{sin 54} = \frac{BE}{sin 108} \Rightarrow BE = \frac{sin 108}{sin 54}. AB[/laTEX]
ta có
[laTEX]sin 108 = sin (2.54) = 2sin 54. cos 54 \\ \\ BE = \frac{2sin 54. cos 54 }{sin 54}.AB = 2cos54.AB[/laTEX]
mặt khác
[laTEX]cos 54 = sin 36 \Rightarrow 2AD = BE[/laTEX]
Tam giác ABC cân tại A có:
ABC=900−10802=900−540=360ABC=900−10802=900−540=360
BE là tia phân giác của ABC
ABE=EBC=ABC2=3602=180ABE=EBC=ABC2=3602=180
AD là tia phân giác của BAC
BAD=DAC=BAC2=10802=540BAD=DAC=BAC2=10802=540
Tam giác ABE có:
ABE+EAB+AEB=1800ABE+EAB+AEB=1800
180+1080+AEB=1800180+1080+AEB=1800
AEB=1800−1260AEB=1800−1260
AEB=540AEB=540
AD là tia phân giác của BAC của tam giác ABC cân tại A
=> AD là trung tuyến của tam giác ABC
Trên tia đối của AC, lấy điểm H sao cho A là trung điểm của HC
mà D là trung điểm của BC (AD là trung tuyến của tam giác ABC)
=> AD là đường trung bình của tam giác CBH
=> AD // HB
=> AHB = EAD (2 góc so le trong)
mà EAD = AEB (= 540)
=> AHB = AEB
=> Tam giác HBE cân tại B
=> HB = BE
mà AD = BH/2 (AD là đường trung bình của tam giác CBH)
=> AD = BE/2 = 10/2 = 5 (cm)
k cho mk nha
chúc bn trung thu vui vẻ
HT