Bài 3: Một vòi nước chảy vào bể không chứa nước, mỗi phút vòi chảy được x lít nước. Cùng lúc đó một vòi khác chảy từ bể ra, mỗi phút chảy ra y lít nước.
a) Viết biểu thức biểu thị lượng nước có trong bể sau a phút.
b) Giả sử sau a phút người ta khóa vòi chảy ra và tiếp tục để vòi chảy vào chảy thêm b phút.
Tính lượng nước trong bể, biết rằng lúc đầu bể chứa 5 lít nước.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(x\) (học sinh) là số học sinh cần tìm \(\left(x\in N;30\le x\le40\right)\)
Do khi xếp hàng 3; 6; 9 đều vừa đủ nên \(x⋮3;x⋮6;x⋮9\)
\(\Rightarrow x\in BC\left(3;6;9\right)\)
Ta có:
\(3=3\)
\(6=2.3\)
\(9=3^2\)
\(\Rightarrow BCNN\left(3;6;9\right)=2.3^2=18\)
\(\Rightarrow x\in\left\{0;18;36;54;...\right\}\)
Mà \(30\le x\le40\)
\(\Rightarrow x=36\)
Vậy lớp 6C có 36 học sinh

xy - 2x + y = 9 (x,y E N)
x(y - 2) + y-2+2 = 9
x(y-2) + (y-2) = 9-2 = 7
(x+1)(y-2) = 7
Suy ra x+1 thuộc Ư(7) = {1;7) (do x E N nên x+1 E N)
TH1 : x+1 = 1
Suy ra y-2 = 7
Suy ra x=0 ; y = 9
Th2: x+1 = 7
Suy ra y-2 = 1
Suy ra x = 6 ; y = 3
Vậy ........

A = 1 x 2 + 2 x 3 + 3 x 4 + ...+ 41 x 42 + 42 x 43
A = \(\dfrac{1}{3}\) x (1 x 2 x 3 + 2 x 3 x 3 + ... + 42 x 43 x 3)
A = \(\dfrac{1}{3}\) x [1 x 2 x 3 + 2 x 3 x (4 - 1)+ ... + 42 x 43 x (44 - 41)]
A = \(\dfrac{1}{3}\) x [1 x 2 x 3 + 2 x 3 x 4 -1 x 2 x 3+...+ 42 x 43 x 44 - 42x43x41]
A = \(\dfrac{1}{3}\) x [42 x 43 x 44]
A = \(\dfrac{42}{3}\) x 43 x 44
A = 14 x 43 x 44
A = 602 x 44
A = 26488

\(A=\left(x^3+3x^2y+3xy^2+y^3\right)-3\left(x^2+2xy+y^2\right)+3\left(x+y\right)+2020\)
\(=\left(x+y\right)^3-3\left(x+y\right)^2+3\left(x+y\right)-1+2021\)
\(=\left(x+y-1\right)^3+2021\)
\(=4040^3+2021\)


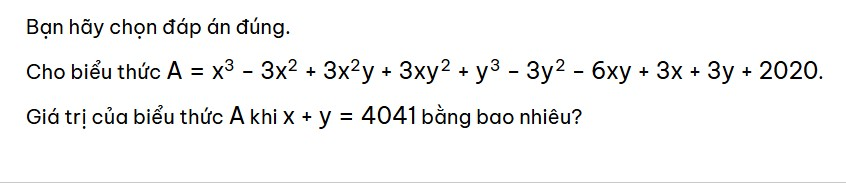
a) Sau a phút, lượng nước có trong bể là:
\(x-y\left(l\right)\)
b) Sau b phút, vòi nước chảy vào được số lít nước là: \(bx\left(l\right)\)
Lượng nước trong bể:
\(5+x-y+bx\left(l\right)\)