Dùng in spite of khi nào vậy mn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, PT: \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
b, Ta có: \(n_{Fe}=\dfrac{19,6}{56}=0,35\left(mol\right)\)
Theo PT: \(n_{H_2}=n_{Fe}=0,35\left(mol\right)\Rightarrow V_{H_2}=0,35.22,4=7,84\left(l\right)\)
c, \(n_{H_2SO_4}=n_{Fe}=0,35\left(mol\right)\Rightarrow C_{M_{H_2SO_4}}=\dfrac{0,35}{0,2}=1,75\left(M\right)\)
d, \(n_{FeSO_4}=n_{Fe}=0,35\left(mol\right)\Rightarrow m_{FeSO_4}=0,35.152=53,2\left(g\right)\)
e, \(C_{M_{FeSO_4}}=\dfrac{0,35}{0,2}=1,75\left(M\right)\)
d, \(n_{H_2SO_4}=0,25.1,6=0,4\left(mol\right)\)
Xét tỉ lệ: \(\dfrac{n_{Fe}}{1}< \dfrac{n_{H_2SO_4}}{1}\), ta được H2SO4 dư.
Theo PT: \(n_{H_2SO_4\left(pư\right)}=n_{Fe}=0,35\left(mol\right)\)
\(\Rightarrow n_{H_2SO_4\left(dư\right)}=0,4-0,35=0,05\left(mol\right)\)
\(\Rightarrow m_{H_2SO_4\left(dư\right)}=0,05.98=4,9\left(g\right)\)

Đề bài phải sửa thành AN=NC mới c/m được
A B C D
MA=MB (gt)
AN=NC (gt)
=> MN là đường trung bình của tg ABC
=> MN//BC và \(MN=\dfrac{BC}{2}\)
Ta có
\(BC\perp AB\) mà MN//BC => \(MN\perp AB\) (1)
Ta có
\(BC=AB\Rightarrow MN=\dfrac{AB}{2}\)
Mà \(MA=MB=\dfrac{AB}{2}\)
=> MN = MA (2)
Từ (1) và (2) => tg AMN vuông cân tại M

\(\sqrt{2}\)\(\times\)\(\sqrt{4}\) - \(\sqrt{15}\) = 2\(\sqrt{2}\) - \(\sqrt{15}\)

Đáp án mà em chọn là sai rồi em nhé.
Em chọn đáp án: (\(\sqrt{7x}\) + \(\sqrt{5}\))2
Đáp án đúng phải là: (\(\sqrt{7}\)\(x\) + \(\sqrt{5}\))2
\(\sqrt{7x}\) và \(\sqrt{7}\)\(x\) khác nhau hoàn toàn em nhé
vì \(\sqrt{7x}\) = \(\sqrt{7}\) \(\times\) \(\sqrt{x}\)
\(\sqrt{7}\)\(x\) = \(\sqrt{7}\) \(\times\) \(x\)
Nên \(\sqrt{7x}\) \(\ne\) \(\sqrt{7}\)\(x\)
Đáp án của em chọn là sai.

Ta thấy 1 cặp tam giác đồng dạng quen thuộc là \(\Delta HAB~\Delta HCA\), từ đó suy ra \(\dfrac{S_{HAB}}{S_{HCA}}=\left(\dfrac{AB}{AC}\right)^2\). Mà ta lại có \(\dfrac{S_{HAB}}{S_{HCA}}=\dfrac{HB}{HC}\) (2 tam giác có chung đường cao hạ từ A) nên suy ra đpcm.
\(\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\sqrt{2}+\sqrt{12}+\sqrt{18-\sqrt{128}}}}}\)

\(\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\sqrt{2}+\sqrt{12}+\sqrt{18-\sqrt{128}}}}}\)
\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\sqrt{2}+2\sqrt{3}+\sqrt{4^2-2.4.\sqrt{2}+\sqrt{2^2}}}}}\)
\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\sqrt{2}+2\sqrt{3}+\sqrt{\left(4-\sqrt{2}\right)^2}}}}\)
\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\sqrt{2}+2\sqrt{3}+\left|4-\sqrt{2}\right|}}}\)
\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\sqrt{2}+2\sqrt{3}+4-\sqrt{2}}}}\)
\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{4+2\sqrt{3}}}}\)
\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\left(\sqrt{3}+1\right)^2}}}\)
\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{3}-1}}\)
\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{2-\sqrt{3}}}\)
\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{4-2\sqrt{3}}}\)
\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{\left(\sqrt{3}-1\right)^2}}\)
\(=\left(\sqrt{3}-1\right)\sqrt{6+2\left|\sqrt{3}-1\right|}\)
\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{3}-2}\)
\(=\left(\sqrt{3}-1\right)\sqrt{4+2\sqrt{3}}\)
\(=\left(\sqrt{3}-1\right)\sqrt{\left(\sqrt{3}+1\right)^2}\)
\(=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)\)
\(=\sqrt{3^2}-1^2\\ =3-1\\ =2\)

\(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{7+4\sqrt{3}}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{\left(2+\sqrt{3}\right)^2}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\left|2+\sqrt{3}\right|}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{3}-20}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{28-10\sqrt{3}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{5^2-2.5.\sqrt{3}+\sqrt{3^2}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{\left(5-\sqrt{3}\right)^2}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\left|5-\sqrt{3}\right|}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+25-5\sqrt{3}}}\)
\(=\sqrt{4+\sqrt{25}}\)
\(=\sqrt{4+5}\)
\(=\sqrt{9}\\ =3\)
\(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{7+4\sqrt{3}}}}}\)
= \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{\left(2+\sqrt{3}\right)^2}}}}\)
= \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10.|2+\sqrt{3}|}}}\)
= \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10.\left(2+\sqrt{3}\right)}}}\)
= \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-20-10\sqrt{3}}}}\)
= \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{28-10\sqrt{3}}}}\)
= \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{\left(5-\sqrt{3}\right)^2}}}\)
= \(\sqrt{4+\sqrt{5\sqrt{3}+5.|5-\sqrt{3}|}}\)
= \(\sqrt{4+\sqrt{5\sqrt{3}+5.\left(5-\sqrt{3}\right)}}\)
= \(\sqrt{4+\sqrt{5\sqrt{3}+25-5\sqrt{3}}}\)
= \(\sqrt{4+\sqrt{25}}\)
= \(\sqrt{4+5}\)
= \(\sqrt{9}\)
= \(3\)


\(e,\dfrac{\sqrt{4x-1}}{\sqrt{7-2x}-2}\) có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}4x-1\ge0\\7-2x\ne4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{4}\\x\ne-\dfrac{3}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{1}{4}\)
\(d,\dfrac{\sqrt{2x-1}}{\sqrt{2x+17}+1}\) có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}2x-1\ge0\\2x+17\ge0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{2}\\x\ge-\dfrac{17}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{1}{2}\)
\(b,c,\dfrac{3}{\sqrt{2x-17}}\) có nghĩa \(\Leftrightarrow2x-17>0\Leftrightarrow x>\dfrac{17}{2}\)
\(a,\sqrt{2-5x}\) có nghĩa \(\Leftrightarrow2-5x\ge0\Leftrightarrow x\le\dfrac{2}{5}\)

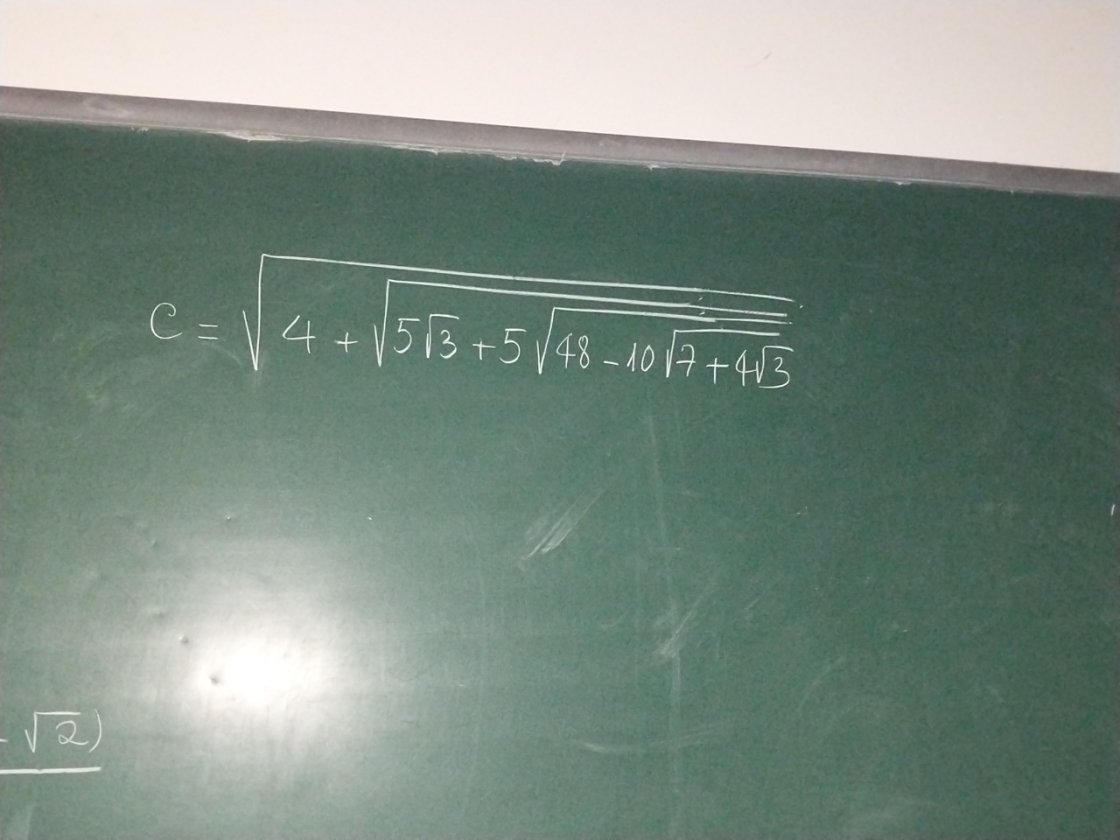
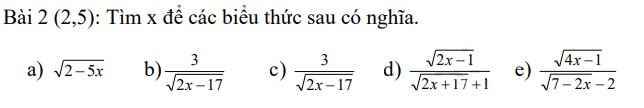
In spite of = Due to + Ving/N, S + V
= In spite of/Due to + the fact that + S + V, S + V
=Although + S + V, S + V
Nghĩa: Mặc dù, biểu thị 2 hành động trái ngược nhau