(2002 - 79 + 15) - (-79 + 15) 

= 2002 - 79 + 15 + 79 - 15

= 2002 + (79 - 79) + (15 - 15) 

= 2002 + 0 + 0

= 2002 

2002 nhé

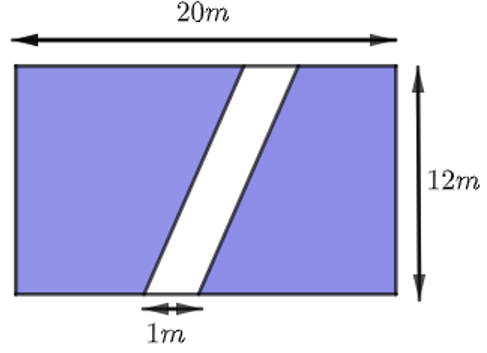
Diện tích khu vườn là:

`20*12=240(m^2)` 

Diện tích lối đi là

`1*12=12(m^2)`

Diện tích trồng hoa là:

`240-12=228(m^2)` 

ĐS: ... 

cảm ơn nhiều ah

ta có 2n+12= 2(n + 6)

suy ra để 2n+12 chia hết cho n+3 thì 

2(n + 6) chia hết cho n+3

nên n + 6 chia hết n +3

rồi làm tiếp nhé :)

Ta có \(n+3⋮n+3\) với mọi số tự nhiên \(n\)

nên \(2\left(n+3\right)=2n+6⋮n+3\)

Mà \(2n+12=2n+6+6\)

Do đó để \(2n+12⋮n+3\) thì \(6⋮n+3\)

nên \(n+3\) thuộc \(U'\left(6\right)=\text{1; 2; 3; 6}\)

Giải từng trường hợp ta được: \(n=0;3\)

\(3^{400}=\left(3^4\right)^{100}=81^{100};5^{300}=\left(5^3\right)^{100}=125^{100}\)

mà 81<125

nên \(3^{400}< 5^{300}\)

Ta có : 

3^400 = (3^4)^100 = 81^100

5^300 = (5^3)^100 = 125^100

Vì 81^100 < 125^100 nên

=>3^400 < 5^300

Vậy 3^400 < 5^300

\(\overline{cab}=3\cdot\overline{ab}+8\)

=>\(100c+10a+b-30a-3b-8=0\)

=>-20a-2b+100c-8=0

=>\(\left(a;b;c\right)\in\left\{\left(4;6;1\right);\left(9;6;2\right)\right\}\)

Vậy: Số cần tìm là 461;962

a: Gọi số ban đầu có dạng là \(\overline{ab7}\)

Số mới được tạo ra khi chuyển chữ số 7 lên đầu là \(\overline{7ab}\)

Chia số mới cho số cũ thì được thương là 2,dư là 21

nên ta có: \(\overline{7ab}=2\cdot\overline{ab7}+21\)

=>\(700+\overline{ab}=2\left(10\overline{ab}+7\right)+21\)
=>\(\overline{ab}-20\overline{ab}=14+21-700\)

=>\(-19\overline{ab}=-665\)

=>\(\overline{ab}=35\)

vậy: Số ban đầu là 357

b: Trong 3 số tự nhiên liên tiếp, chắc chắn sẽ có số chia hết cho 3

=>Tích của 3 số tự nhiên liên tiếp sẽ luôn chia hết cho 3

Gọi số cần tìm là \(\overline{abc}\)

Viết thêm số 50 vào bên trái thì lấy số mới chia số ban đầu thì được thương là 401 nên \(\overline{50abc}=401\cdot\overline{abc}\)

=>\(50000+\overline{abc}=401\cdot\overline{abc}\)

=>\(400\cdot\overline{abc}=50000\)

=>\(\overline{abc}=125\)

Vậy: Số cần tìm là 125

a: \(2\cdot5^2+3:71^0-54:3^3\)

\(=2\cdot25+3:1-54:27\)

=50+3-2=51

b: \(36\cdot4-4\cdot\left(82-7\cdot11\right)^2:4-2016^0\)

\(=144-\left(82-77\right)^2-1\)

\(=143-5^2=143-25=118\)

a: Vì AB//CD

nên \(\dfrac{MB}{MC}=\dfrac{AB}{DC}=\dfrac{1}{3}\)

=>\(\dfrac{S_{BAM}}{S_{MAC}}=\dfrac{1}{3}\)

b: Vì AB//CD

nên ΔMAB~ΔMDC

=>\(\dfrac{S_{MAB}}{S_{MDC}}=\left(\dfrac{AB}{DC}\right)^2=\dfrac{1}{9}\)

=>\(S_{MAB}=\dfrac{1}{9}\cdot S_{MDC}\)

=>\(\dfrac{S_{MAB}}{S_{ABCD}}=\dfrac{1}{8}\)

=>\(\dfrac{S_{MAB}}{64}=\dfrac{1}{8}\)

=>\(S_{MAB}=\dfrac{64}{8}=8\left(cm^2\right)\)