\(\frac{1}{x\left(x+1\right)}+\frac{1}{\left(x+1\right)\left(x+2\right)}+\frac{1}{\left(x+2\right)\left(x+3\right)}-\frac{1}{x}=\frac{1}{2010}\)

\(\frac{1}{x}-\frac{1}{x+1}+\frac{1}{x+1}-\frac{1}{x+2}+\frac{1}{x+2}-\frac{1}{x+3}-\frac{1}{x}=\frac{1}{2010}\)

\(\frac{-1}{x+3}=\frac{1}{2010}\)

\(\Rightarrow-\left(x-3\right)=2010\)

\(\Rightarrow x=-2013\)

\(\frac{1}{x\left(x+1\right)}+\frac{1}{\left(x+1\right)\left(x+2\right)}+\frac{1}{\left(x+2\right)\left(x+3\right)}-\frac{1}{x}=\frac{1}{2010}\)

\(\Rightarrow\frac{1}{x}-\frac{1}{x+1}+\frac{1}{x+1}-\frac{1}{x+2}+\frac{1}{x+2}-\frac{1}{x+3}-\frac{1}{x}=\frac{1}{2010}\)

\(\Rightarrow\frac{1}{x}-\frac{1}{x+3}-\frac{1}{x}=\frac{1}{2010}\)

\(\Rightarrow\left(\frac{1}{x}-\frac{1}{x}\right)-\frac{1}{x+3}=\frac{1}{2010}\)

\(\Rightarrow\frac{1}{x+3}=\frac{1}{2010}\)

\(\Rightarrow x=2007\)

( x - 3/2 ) ( 2x + 1 ) > 0

TH1 : cả 2 thừa số đều lớn hơn 0

\(\Rightarrow\hept{\begin{cases}x-\frac{3}{2}>0\\2x+1>0\end{cases}\Rightarrow\hept{\begin{cases}x>\frac{3}{2}\\x>-\frac{1}{2}\end{cases}\Rightarrow}x>\frac{3}{2}}\)

TH2 : cả 2 thừa số đều bé hơn 0

\(\Rightarrow\hept{\begin{cases}x-\frac{3}{2}< 0\\2x+1< 0\end{cases}\Rightarrow\hept{\begin{cases}x< \frac{3}{2}\\x< -\frac{1}{2}\end{cases}\Rightarrow}x< -\frac{1}{2}}\)

Vậy,..........

\(\frac{x+1}{10}+\frac{x+2}{9}+\frac{x+3}{8}+\frac{x+4}{7}+\frac{x+5}{6}=-5\)

\(\left(\frac{x+1}{10}+1\right)+\left(\frac{x+2}{9}+1\right)+\left(\frac{x+3}{8}+1\right)+\left(\frac{x+4}{7}+1\right)+\left(\frac{x+5}{6}+1\right)=0\)

\(\frac{x+11}{10}+\frac{x+11}{9}+\frac{x+11}{8}+\frac{x+11}{7}+\frac{x+12}{6}=0\)

\(\left(x+11\right)\left(\frac{1}{10}+\frac{1}{9}+\frac{1}{8}+\frac{1}{7}+\frac{1}{6}\right)=0\)

Vì : \(\frac{1}{10}+\frac{1}{9}+\frac{1}{8}+\frac{1}{7}+\frac{1}{6}>0\)

\(\Rightarrow x+11=0\)

\(\Rightarrow x=-11\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có :

\(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{2x+y-z}{4+3-5}=\frac{8}{2}=4\)

\(\Rightarrow\hept{\begin{cases}\frac{x}{2}=4\\\frac{y}{3}=4\\\frac{z}{5}=4\end{cases}\Rightarrow\hept{\begin{cases}x=8\\y=12\\z=20\end{cases}}}\)

Vậy,_

\(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\)

\(\Rightarrow\frac{2x}{4}=\frac{y}{3}=\frac{z}{5}\)

áp dụng t\c của dãy tỉ số bằng nhau ta có :

\(\frac{2x}{4}=\frac{y}{3}=\frac{z}{5}=\frac{2x+y-z}{4+3-5}=\frac{8}{2}=4\)

\(\Rightarrow\hept{\begin{cases}x=4\cdot2=8\\y=4\cdot3=12\\z=4\cdot5=20\end{cases}}\)

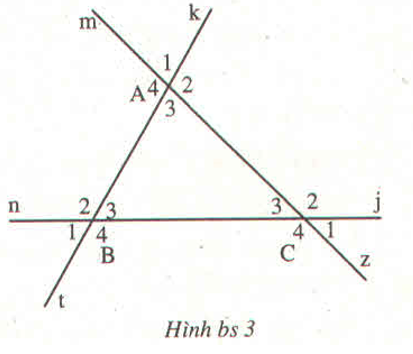
Méo thấy hình :D

Cho hình mà chẳng vẽ thì có thánh thần mới làm được.

hỏi gì mà ngáo thế

cÂU HỎI HƠI LẠ

Giải

Số gạo đã cứu trợ bão lụt là: 36 x \(\dfrac{2}{3}\) = 24 (tấn)

Sau khi cứu trợ, bán đi và nhập thêm số gạo còn lại trong kho là:

 36 - 24 - \(\dfrac{19}{4}\) + 4 = \(\dfrac{45}{4}\) (tấn)

Kết luận: Cuối cùng số gạo còn lại trong kho là: \(\dfrac{45}{4}\) tấn

Bài 1 :

Nếu a ≥ 0

a, |a | + a = a + a = 2a

b, | a | - a =  a - a = 0

c, | a | : a = a : a = 1

Nếu a < 0

a, | a | + a = - a + a = 0

b, | a | -a = -a - a = -2a 

c, | a | : a =  -a : a = -1

Bài 2 :

\(\orbr{\begin{cases}2x-1=2x+3\\1-2x=2x+3\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}0x=4\\-4x=2\end{cases}\Leftrightarrow\orbr{\begin{cases}x\in\varnothing\\x=\frac{-1}{2}\end{cases}}}\)

Vậy x = -1/2