
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. \(8x\left(x-2007\right)-2x+4034=0\)
\(\Rightarrow\left(x-2017\right)\left(4x-1\right)\)
\(\Rightarrow\left[{}\begin{matrix}x-2017=0\\4x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2017\\4x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2017\\x=\dfrac{1}{4}\end{matrix}\right.\)
Vậy x=2017 hoặc x=1/4
b.\(\dfrac{x}{2}+\dfrac{x^2}{8}=0\)
\(\Rightarrow\dfrac{x}{2}\left(1+\dfrac{x}{4}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{x}{2}=0\\1+\dfrac{x}{4}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\\dfrac{x}{4}=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
Vậy x=0 hoặc x=-4
c.\(4-x=2\left(x-4\right)^2\)
\(\Rightarrow\left(4-x\right)-2\left(x-4\right)^2=0\)
\(\Rightarrow\left(4-x\right)\left(2x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4-x=0\\2x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{7}{2}\end{matrix}\right.\)
Vậy x=4 hoặc x=7/2
d.\(\left(x^2+1\right)\left(x-2\right)+2x=4\)
\(\Rightarrow\left(x-2\right)\left(x^2+3\right)=0\)
Nxet: (x2+3)>0 với mọi x
=> x-2=0 <=>x=2
Vậy x=2
a, 8\(x\).(\(x-2007\)) - 2\(x\) + 4034 = 0
4\(x\)(\(x\) - 2007) - \(x\) + 2017 = 0
4\(x^2\) - 8028\(x\) - \(x\) + 2017 = 0
4\(x^2\) - 8029\(x\) + 2017 = 0
4(\(x^2\) - 2. \(\dfrac{8029}{8}\) \(x\) +( \(\dfrac{8029}{8}\))2) - (\(\dfrac{8029}{4}\))2 + 2017 = 0
4.(\(x\) + \(\dfrac{8029}{8}\))2 = (\(\dfrac{8029}{4}\))2 - 2017
\(\left[{}\begin{matrix}x=-\dfrac{8029}{8}+\dfrac{1}{2}.\sqrt{\left(\dfrac{8029}{4}\right)^2-2017}\\x=-\dfrac{8029}{8}-\dfrac{1}{2}.\sqrt{\left(\dfrac{8029}{4}\right)^2-2017}\end{matrix}\right.\)

a, F(\(x\)) = a\(x^2\) + b\(x\) + c (a; b; c \(\in\) Q và a \(\ne\) 0)
Vì F(\(x\)) có nghiệm là \(\sqrt{2}\) ta có F(\(\sqrt{2}\)) = 0
⇔ a.(\(\sqrt{2}\))2 + b.(\(\sqrt{2}\)) + c = 0
2a + \(\sqrt{2}\)b + c = 0 ⇒ c = - (2a + \(\sqrt{2}\)b) (1)
a\(x^2\) + b\(x\) + c = 0
a(\(x^2\) + 2. \(\dfrac{b}{2a}\)\(x\) + \(\dfrac{b^2}{4a^2}\)) - \(\dfrac{b^2-4ac}{4a}\) = 0
a.(\(x\) + \(\dfrac{b}{2a}\))2 = \(\dfrac{b^2-4ac}{4a}\)
(\(x\) + \(\dfrac{b}{2a}\) )2 = \(\dfrac{b^2-4ac}{4a^2}\)
\(\left[{}\begin{matrix}x=\dfrac{-b+\sqrt{b^2-4ac}}{2a}\\x=\dfrac{-b-\sqrt{b^2-4ac}}{2a}\end{matrix}\right.\)
Thay (1) vào \(x\) = \(\dfrac{-b-\sqrt{b^2-4ac}}{2a}\) ta có
\(x\) = \(\dfrac{-b-\sqrt{b^2-4a\left(2a+\sqrt{2}b\right)}}{2a}\)
a) \(f\left(x\right)=ax^2+bx+c=0\)
\(\Rightarrow f\left(x_1=\sqrt[]{2}\right)=2a+b\sqrt[]{2}+c=0\left(1\right)\)
\(S=x_1+x_2=-\dfrac{b}{a}\Rightarrow x_2=-\dfrac{b}{a}-x_1=-\dfrac{b}{a}-\sqrt[]{2}\)
\(P=x_1.x_2=\dfrac{c}{a}\Rightarrow x_2=\dfrac{c}{a.x_1}=\dfrac{c}{a.\sqrt[]{2}}\)
Vậy nghiệm còn lại là \(-\dfrac{b}{a}-\sqrt[]{2}\) hay \(\dfrac{c}{a.\sqrt[]{2}}\left(a,b,c\in Q;a\ne0\right)\)
b) \(P\left(x\right)=x^2-px+q\)
\(S=x_1+x_2=p;P=x_1.x_2=q\)
Để P(x) có nghiệm \(x_1;x_2\) đều là số nguyên
\(\Rightarrow S=p;P=q\) đều là số nguyên
mà \(p,q\) là số nguyên tố
\(\Rightarrow p;q⋮1\)
\(\Rightarrow\left(p;q\right)\in\left\{-1;1\right\}\Rightarrow p=\pm1;q=\pm1\)
Ta thay \(p=\pm1;q=\pm1\) vào \(P\left(x\right)=x^2-px+p=0\) ta được \(\Delta=5;\Delta=-4< 0\) \(\Rightarrow p,q\) không thỏa nghiệm đa thức nguyên
\(\Rightarrow\left(p;q\right)\in\varnothing\)

Hình của em đâu, phần tô màu là phần nào thì mới chứng minh chính xác được em nhé

\(\dfrac{3}{4}\left(x^2y\right)^2:\dfrac{1}{8}xy^2\\ =\dfrac{3}{4}x^4y^2:\dfrac{1}{8}xy^2\\ =\left(\dfrac{3}{4}:\dfrac{1}{8}\right)\left(x^4:x\right)\left(y^2:y^2\right)\\ =6x^3\)
\(\dfrac{3}{4}\left(x^2y\right)^2\div\dfrac{1}{8}xy^2\)
\(=\dfrac{3}{4}x^4y^2\div\dfrac{1}{8}xy^2\)
\(=6x^3\)

a) Vì AB//CD, ta có góc ACD = góc BCD = 180 - góc D = 180 - 60 = 120 độ.
Vì AB//CD, ta có góc ACD = góc BAD.
Vậy số đo góc A là 120 độ.
b) Gọi góc BCD là x độ.
Theo giả thiết, góc B phần góc D = 4/5, ta có:
góc B = (4/5) * góc D
= (4/5) * 60
= 48 độ.
Vì AB//CD, ta có góc BCD = góc BAD.
Vậy góc BAD = góc BCD = x độ.
Vì tứ giác ABCD là tứ giác lồi, tổng các góc trong tứ giác ABCD là 360 độ.
Ta có: góc A + góc B + góc C + góc D = 360 độ.
Vì góc D = 60 độ, góc A = 120 độ và góc B = 48 độ, ta có:
120 + 48 + góc C + 60 = 360
góc C = 360 - 120 - 48 - 60 = 132 độ.
Vậy số đo góc B là 48 độ và số đo góc C là 132 độ.
* Ib = bài 4

cô làm rồi em ơi https://olm.vn/cau-hoi/bai-3-tu-giac-abcd-co-goc-c-goc-d-90-do-chung-minh-rang-ac2-bd-ab2cd2.8140260328277

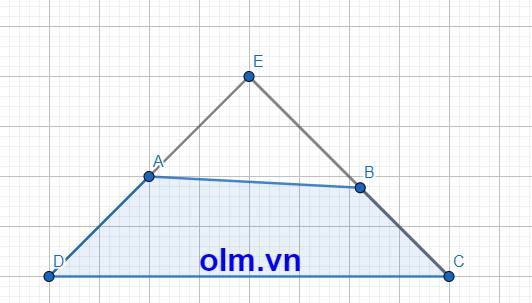
Kéo dài DA và CB lần lượt về phía A và B cắt nhau tại E
Xét tam giác DCE có \(\widehat{DEC}\) = 1800 - (\(\widehat{EDC}\) + \(\widehat{ECD}\)) = 1800- 900 = 900
⇒\(\Delta\)DEC vuông tại E
Xét \(\Delta\)AEB Theo pytago ta có: AE2 + BE2 = AB2
Tương tự ta có: DE2 + CE2 = DC2
Cộng vế với vế ta có: AE2 + BE2 + DE2 + CE2 = AB2+DC2
AE2 + CE2+BE2+DE2 = AB2+DC2 (1)
Xét \(\Delta\)AEC theo pytago ta có: AE2+ CE2 = AC2
Tương tự ta có: BE2 + DE2 = BD2
Cộng vế với vế ta có: AE2 + CE2 + BE2+ DE2 = AC2 + BD2 (2)
Từ (1) và (2) ta có: AC2 + BD2 = AB2 + DC2(đpcm)

Bài 1:
a) Sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác OAB, OBC,OCD và ODA.
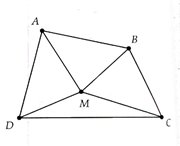
b) Chứng minh tổng hai đường chéo lớn hơn nửa chu vi tứ giác sử dụng kết quả của a).
Chứng minh tổng hai đường chéo nhỏ hơn chu vi tứ giác sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác ABC, ADC, ABD và CBD
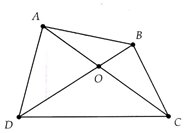
Bài 3:
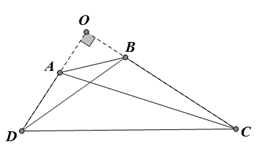
Gọi O là giao điểm AD và BC.
Ta có ˆC+⌢D=900�^+�⏜=900 nên ˆO=900�^=900
Áp dụng định lí Py – ta – go,
Ta có
AC2=OA2+OC2.��2=��2+��2.
BD2=OB2+OD2��2=��2+��2
Nên AC2+BD2=(OA2+OB2)+(OC2+OD2)=AB2+CD2
Bài 1: 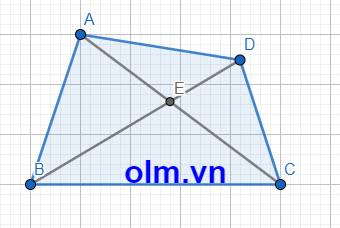
Gọi E là giao điểm của hai đường chéo AC và BD
Xét tam giác AEB ta có: AE + BE > AB (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét tam giác DEC ta có: DE + CE > DC (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AE + BE + DE + CE > AB + DC
(AE + CE) + (BE + DE) > AB + DC
AC + BD > AB + DC
Tương tự ta có AC + BD > AD + BC
Kết luận: Trong một tứ giác tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối.
Nửa chu vi của tứ giác ABCD là: \(\dfrac{AB+BC+CD+DA}{2}\)
Theo chứng minh trên ta có:
\(\dfrac{AB+BC+CD+DA}{2}\)< \(\dfrac{\left(AB+CD\right)\times2}{2}\) = AB + CD (1)
Vì trong một tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại nên ta có:
AB + AD > BD
AB + BC > AC
BC + CD > BD
CD + AD > AC
Cộng vế với vế ta có:
(AB + BC + CD + DA)\(\times\)2 > (BD + AC ) \(\times\) 2
⇒AB + BC + CD + DA > BD + AC (2)
Kết hợp (1) và (2) ta có:
Tổng hai đường chéo của tứ giác lớn hơn nửa chu vi của tứ giác nhưng nhỏ hơn chu vi của tứ giác

