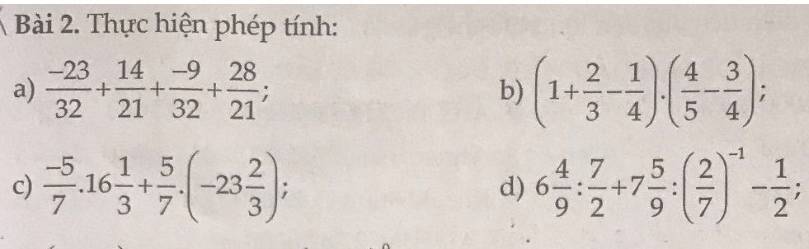
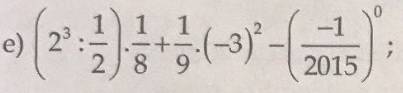
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: `3/4=0,75` và `3/5=0,6`
Ta cần viết các số hữu tỉ nhỏ hơn 0,75 và lớn hớn 0,6
\(0,65=\dfrac{13}{20}\)
\(0,7=\dfrac{7}{10}\)
\(0,72=\dfrac{18}{25}\)
b) Ta có: `2/3=0,66...` và `3/4=0,75`
Ta cần viết các số hữu tỉ nhỏ hơn 0,75 và lớn hơn 0,66...
\(0,68=\dfrac{17}{25}\)
\(0,7=\dfrac{7}{10}\)
\(0,72=\dfrac{18}{25}\)

a)
\(\dfrac{267}{268}< 1\Rightarrow-\dfrac{267}{268}>-1\)
\(\dfrac{1347}{1343}>1\Rightarrow-\dfrac{1347}{1343}< -1\)
\(\Rightarrow-\dfrac{1347}{1343}< -\dfrac{267}{268}\)
b) \(\dfrac{2022\cdot2023-1}{2022\cdot2023}=\dfrac{2022\cdot2023}{2022\cdot2023}-\dfrac{1}{2022\cdot2023}=1-\dfrac{1}{2022\cdot2023}\)
\(\dfrac{2023\cdot2024-1}{2023\cdot2024}=\dfrac{2023\cdot2024}{2023\cdot2024}-\dfrac{1}{2023\cdot2024}=1-\dfrac{1}{2023\cdot2024}\)
Vì: \(2022\cdot2023< 2023\cdot2024\)
\(\Rightarrow\dfrac{1}{2022\cdot2023}>\dfrac{1}{2023\cdot2024}\)
\(\Rightarrow1-\dfrac{1}{2022\cdot2023}< 1-\dfrac{1}{2023\cdot2024}\)
Hay: `(2022*2023-1)/(2022*2023) < (2023*2024 - 1)/(2023*2024)`
c) \(\dfrac{2022\cdot2023}{2022\cdot2023+1}=\dfrac{2023\cdot2023+1-1}{2022\cdot2023+1}=1-\dfrac{1}{2022\cdot2023+1}\)
\(\dfrac{2023\cdot2024}{2023\cdot2024+1}=\dfrac{2023\cdot2024+1-1}{2023\cdot2024+1}=1-\dfrac{1}{2023\cdot2024+1}\)
Vì: \(2022\cdot2023+1< 2023\cdot2024+1\)
\(\Rightarrow\dfrac{1}{2022\cdot2023+1}>\dfrac{1}{2023\cdot2024+1}\)
\(\Rightarrow1-\dfrac{1}{2022\cdot2023+1}< 1-\dfrac{1}{2023\cdot2024+1}\)
Hay: `(2022*2023)/(2022*2023+1)<(2023*2024)/(2023*2024+1)`


\(\dfrac{x^3-3x^2y+3xy^2-y^3}{x-y}=\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)-3xy\left(x-y\right)}{x-y}\)
\(=\dfrac{\left(x-y\right)\left(x^2-2xy+y^2\right)}{x-y}=\left(x-y\right)^2\)

a: Xét ΔBAD vuông tại A và ΔBMD vuông tại M có
BD chung
\(\widehat{ABD}=\widehat{MBD}\)
Do đó: ΔBAD=ΔBMD
b: ΔBAD=ΔBMD
=>DA=DM
mà DM<DC(ΔDMC vuông tại M)
nên DA<DC
c: ΔBAD=ΔBMD
=>BA=BM
=>ΔBAM cân tại B
Ta có: ΔBAM cân tại B
mà BI là đường phân giác
nên BI\(\perp\)AM và I là trung điểm của AM
Ta có: BI\(\perp\)AM
ME\(\perp\)AM
Do đó: ID//ME
Xét ΔAME có
I là trung điểm của AM
ID//ME
Do đó: D là trung điểm của AE
Xét ΔAME có
AK,EI,MD là các đường trung tuyến
Do đó: AK,EI,MD đồng quy

a) Nữa chu vi mảnh đất là:
90 : 2 = 45 (m)
Tổng số phần bằng nhau là:
2 + 3 = 5 (phần)
Chiều rộng là:
45 : 5 x 2 = 18 (m)
Chiều dài là:
45 - 18 = 27 (m)
Diện tích mảnh đất là:
18 x 27 = 486 `(m^2)`
b) Diện tích trồng rau là:
20% x 486 = 97,2 `(m^2)`
Diện tích trồng hoa là:
`2/9 xx 486 = 108 (m^2)`
Diện tích trồng cây ăn quả là:
486 - 97,2 - 108 = 280,8 `(m^2)`
ĐS: ...

2B.
a) \(A=\dfrac{\dfrac{1}{3}-\dfrac{1}{7}-\dfrac{1}{13}}{\dfrac{2}{3}-\dfrac{2}{7}-\dfrac{2}{13}}\cdot\dfrac{\dfrac{3}{4}-\dfrac{3}{16}-\dfrac{3}{64}-\dfrac{3}{256}}{1-\dfrac{1}{4}-\dfrac{1}{16}-\dfrac{1}{64}}+\dfrac{5}{8}\)
\(=\dfrac{\dfrac{1}{3}-\dfrac{1}{7}-\dfrac{1}{13}}{2\left(\dfrac{1}{3}-\dfrac{1}{7}-\dfrac{1}{13}\right)}\cdot\dfrac{\dfrac{3}{4}\cdot\left(1-\dfrac{1}{4}-\dfrac{1}{16}-\dfrac{1}{64}\right)}{1-\dfrac{1}{4}-\dfrac{1}{16}-\dfrac{1}{64}}+\dfrac{5}{8}\)
\(=\dfrac{1}{2}\cdot\dfrac{3}{4}+\dfrac{5}{8}\)
\(=\dfrac{3}{8}+\dfrac{5}{8}\)
\(=\dfrac{8}{8}\)
\(=1\)
b) \(B=\dfrac{0,125-\dfrac{1}{5}+\dfrac{1}{7}}{0,375-\dfrac{3}{5}+\dfrac{3}{7}}+\dfrac{\dfrac{1}{2}+\dfrac{1}{3}-0,2}{\dfrac{3}{4}+0,5-\dfrac{3}{10}}\)
\(=\dfrac{\dfrac{1}{8}-\dfrac{1}{5}-\dfrac{1}{7}}{\dfrac{3}{8}-\dfrac{3}{5}+\dfrac{3}{7}}+\dfrac{\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{5}}{\dfrac{3}{4}+\dfrac{1}{2}-\dfrac{3}{10}}\)
\(=\dfrac{\dfrac{1}{8}-\dfrac{1}{5}+\dfrac{1}{7}}{3\left(\dfrac{1}{8}-\dfrac{1}{5}+\dfrac{1}{7}\right)}+\dfrac{2\cdot\left(\dfrac{1}{4}+\dfrac{1}{6}-\dfrac{1}{10}\right)}{\dfrac{3}{4}+\dfrac{3}{6}-\dfrac{3}{10}}\)
\(=\dfrac{1}{3}\cdot\dfrac{2\left(\dfrac{1}{4}+\dfrac{1}{6}-\dfrac{1}{10}\right)}{3\left(\dfrac{1}{4}+\dfrac{1}{6}-\dfrac{1}{10}\right)}\)
\(=\dfrac{1}{3}\cdot\dfrac{2}{3}\)
\(=\dfrac{2}{9}\)
3A:
\(A=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{10}-1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-9}{10}=\dfrac{-1}{10}>-\dfrac{1}{9}\)
3B:
\(B=\left(\dfrac{1}{4}-1\right)\left(\dfrac{1}{9}-1\right)\cdot...\cdot\left(\dfrac{1}{100}-1\right)\)
\(=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{10}-1\right)\cdot\left(\dfrac{1}{2}+1\right)\cdot\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{10}+1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-9}{10}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{11}{10}\)
\(=\dfrac{-1}{10}\cdot\dfrac{11}{2}=\dfrac{-11}{20}\)
Vì 20<21 nên \(\dfrac{11}{20}>\dfrac{11}{21}\)
=>\(-\dfrac{11}{20}< -\dfrac{11}{21}\)
=>\(B< -\dfrac{11}{21}\)
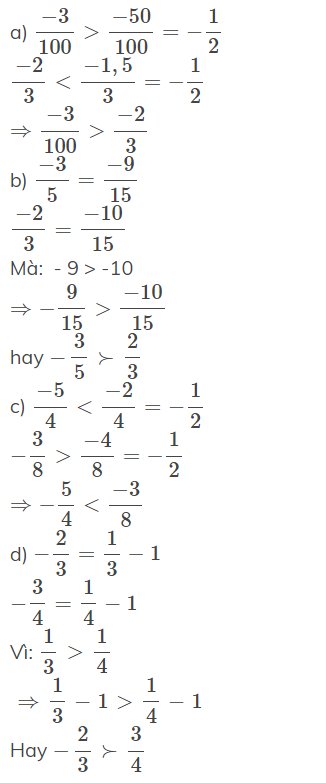



Bài 3:
a)
\(\dfrac{2}{3}x+4=-12\\ \Rightarrow\dfrac{2}{3}x=-12-4=-16\\ \Rightarrow x=-16:\dfrac{2}{3}\Rightarrow x=-24\)
b) \(\dfrac{5}{6}-\dfrac{1}{6}:x=-2\dfrac{1}{2}\)
\(\Rightarrow\dfrac{5}{6}-\dfrac{1}{6}:x=-\dfrac{3}{2}\\ \Rightarrow\dfrac{1}{6}:x=\dfrac{5}{6}+\dfrac{3}{2}\\ \Rightarrow\dfrac{1}{6}:x=\dfrac{14}{6}\\ \Rightarrow x=\dfrac{1}{6}:\dfrac{14}{6}=\dfrac{1}{14}\)
c) \(x:20-25\%x=-1\dfrac{1}{5}\)
\(\Rightarrow\dfrac{x}{20}-\dfrac{x}{4}=-\dfrac{4}{5}\)
\(\Rightarrow\dfrac{x}{20}-\dfrac{5x}{20}=-\dfrac{4}{5}\)
\(\Rightarrow-\dfrac{4x}{20}=\dfrac{-4}{5}\)
\(\Rightarrow-\dfrac{x}{5}=-\dfrac{4}{5}\)
\(\Rightarrow x=-4\)
d) \(\dfrac{35}{x-1}=\dfrac{15}{-6}\left(x\ne1\right)\)
\(\Rightarrow-6\cdot35=15\left(x-1\right)\\ \Rightarrow-210=15x-15\\ \Rightarrow15x=-210+15=-195\\ \Rightarrow x=\dfrac{-195}{15}\\ \Rightarrow x=-13\)
e)
\(\left(\dfrac{9}{25}\right)^x=\left(\dfrac{5}{3}\right)^{-1}\cdot\left(\dfrac{3}{5}\right)^5\\ \Rightarrow\left[\left(\dfrac{3}{5}\right)^2\right]^x=\dfrac{3}{5}\cdot\left(\dfrac{3}{5}\right)^5\\ \Rightarrow\left(\dfrac{3}{5}\right)^{2x}=\left(\dfrac{3}{5}\right)^6\\ \Rightarrow2x=6\\ \Rightarrow x=3\)
f)
\(0,5^{x+1}+0,5^x=1,5\\ \Rightarrow0,5^x\cdot\left(0,5+1\right)=1,5\\ \Rightarrow0,5^x\cdot1,5=1,5\\ \Rightarrow0,5^x=1,5:1,5=1\\ \Rightarrow0,5^x=0,5^0\\ \Rightarrow x=0\)
Bài 3:
a: \(\dfrac{2}{3}x+4=-12\)
=>\(\dfrac{2}{3}x=-12-4=-16\)
=>\(x=-16:\dfrac{2}{3}=-16\cdot\dfrac{3}{2}=-24\)
b: \(\dfrac{5}{6}-\dfrac{1}{6}:x=-2\dfrac{1}{2}\)
=>\(\dfrac{5}{6}-\dfrac{1}{6}:x=-\dfrac{5}{2}\)
=>\(\dfrac{1}{6}:x=\dfrac{5}{6}+\dfrac{5}{2}=\dfrac{5}{6}+\dfrac{15}{6}=\dfrac{20}{6}=\dfrac{10}{3}\)
=>\(x=\dfrac{1}{6}:\dfrac{10}{3}=\dfrac{1}{6}\cdot\dfrac{3}{10}=\dfrac{1}{20}\)
c: \(x:20-25\%\cdot x=-1\dfrac{1}{5}\)
=>\(0,05x-0,25x=-1,2\)
=>-0,2x=-1,2
=>x=1,2:0,2=6
d: \(\dfrac{35}{x-1}=\dfrac{15}{-6}\)(ĐKXĐ: \(x\ne1\))
=>\(x-1=\dfrac{35\cdot\left(-6\right)}{15}=\dfrac{-210}{15}=-14\)
=>x=-14+1=-13(nhận)
e: \(\left(\dfrac{9}{25}\right)^x=\left(\dfrac{5}{3}\right)^{-1}\cdot\left(\dfrac{3}{5}\right)^5\)
=>\(\left(\dfrac{3}{5}\right)^{2x}=\left(\dfrac{3}{5}\right)\cdot\left(\dfrac{3}{5}\right)^5=\left(\dfrac{3}{5}\right)^6\)
=>2x=6
=>x=3
f: \(0,5^{x+1}+0,5^x=1,5\)
=>\(0,5^x\cdot\left(0,5+1\right)=1,5\)
=>\(0,5^x=1\)
=>x=0
Bài 2:
a: \(\dfrac{-23}{32}+\dfrac{14}{21}+\dfrac{-9}{32}+\dfrac{28}{21}\)
\(=\left(-\dfrac{23}{32}-\dfrac{9}{32}\right)+\left(\dfrac{14}{21}+\dfrac{28}{21}\right)\)
\(=-\dfrac{32}{32}+\dfrac{42}{21}=-1+2=1\)
b: \(\left(1+\dfrac{2}{3}-\dfrac{1}{4}\right)\cdot\left(\dfrac{4}{5}-\dfrac{3}{4}\right)\)
\(=\left(\dfrac{12}{12}+\dfrac{8}{12}-\dfrac{3}{12}\right)\cdot\left(\dfrac{16}{20}-\dfrac{15}{20}\right)\)
\(=\dfrac{17}{12}\cdot\dfrac{1}{20}=\dfrac{17}{240}\)
c: \(\dfrac{-5}{7}\cdot16\dfrac{1}{3}+\dfrac{5}{7}\cdot\left(-23\dfrac{2}{3}\right)\)
\(=\dfrac{-5}{7}\cdot\left(16+\dfrac{1}{3}+23+\dfrac{2}{3}\right)\)
\(=-\dfrac{5}{7}\cdot40=-\dfrac{200}{7}\)
d: \(6\dfrac{4}{9}:\dfrac{7}{2}+7\dfrac{5}{9}:\left(\dfrac{2}{7}\right)^{-1}-\dfrac{1}{2}\)
\(=\left(6+\dfrac{4}{9}\right)\cdot\dfrac{2}{7}+\left(7+\dfrac{5}{9}\right)\cdot\dfrac{2}{7}-\dfrac{1}{2}\)
\(=\dfrac{2}{7}\left(6+\dfrac{4}{9}+7+\dfrac{5}{9}\right)-\dfrac{1}{2}=\dfrac{2}{7}\cdot14-\dfrac{1}{2}=4-\dfrac{1}{2}=\dfrac{7}{2}\)
e: \(\left(2^3:\dfrac{1}{2}\right)\cdot\dfrac{1}{8}+\dfrac{1}{9}\cdot\left(-3\right)^2-\left(-\dfrac{1}{2015}\right)^0\)
\(=\left(8\cdot2\right)\cdot\dfrac{1}{8}+\dfrac{1}{9}\cdot9-1=2+1-1=2\)