




Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Em ơi chia hết cho 4 thì làm sao lại dư 1 được nữa em.
Gọi a là số cần tìm
Vì a chia 4 dư 1 nên a là số lẻ
Nhưng theo đề bài, a là số chẵn
nên không có số nào thỏa đề bài

\(500-\left\{5\cdot\left[409-\left(2^3\cdot3-21\right)^2\right]-1724\right\}\\ =500-\left\{5\cdot\left[409-\left(8\cdot3-21\right)^2\right]-1724\right\}\\ =500-\left\{5\cdot\left[409-\left(24-21\right)^2\right]-1724\right\}\\ =500-\left[5\cdot\left(409-3^2\right)-1724\right]\\ =500-\left[5\cdot\left(409-9\right)-1724\right]\\ =500-\left(5\cdot400-1724\right)\\ =500-\left(2000-1724\right)\\ =500-276\\ =224\)
\(500-\left\{5\left[409-\left(2^3\times3-21\right)^2\right]-1724\right\}\)
\(=500-\left\{5\left[409-\left(24-21\right)^2\right]-1724\right\}\)
\(=500-\left\{5\left[409-9\right]-1724\right\}\)
\(=500-\left\{5.400-1724\right\}\)
\(=500-\left\{2000-1724\right\}\)
\(=500-2000+1724\)
\(=224\)

\(a.\dfrac{2}{3}-\left(-\dfrac{1}{2}-x\right)=-\dfrac{4}{5}\\ \dfrac{2}{3}+\dfrac{1}{2}+x=-\dfrac{4}{5}\\ x=-\dfrac{4}{5}-\dfrac{2}{3}-\dfrac{1}{2}\\ x=-\dfrac{59}{30}\\ b.\left(-x-3\dfrac{1}{4}\right)-\left(1\dfrac{2}{3}-2\dfrac{3}{4}\right)=\dfrac{-5}{6}\\ \left(-x-\dfrac{13}{4}\right)-\left(\dfrac{5}{3}-\dfrac{11}{4}\right)=\dfrac{-5}{6}\\ -x-\dfrac{13}{4}-\dfrac{5}{3}+\dfrac{11}{4}=-\dfrac{5}{6}\\ -x-\dfrac{5}{3}-\dfrac{1}{2}=-\dfrac{5}{6}\\ x=\dfrac{5}{6}-\dfrac{5}{3}-\dfrac{1}{2}\\ x=-\dfrac{4}{3}\\ c.\dfrac{8}{23}\cdot\dfrac{46}{24}-\dfrac{1}{2}x=\dfrac{1}{3}\\ \dfrac{2}{3}-\dfrac{1}{2}x=\dfrac{1}{3}\\ \dfrac{1}{2}x=\dfrac{2}{3}-\dfrac{1}{3}=\dfrac{1}{3}\\ x=\dfrac{1}{3}:\dfrac{1}{2}=\dfrac{2}{3}\\ d.\dfrac{x-1}{16}=\dfrac{3}{x+1}\\ \left(x-1\right)\left(x+1\right)=3\cdot16=48\\ x^2-1=48\\ x^2=49\\ x^2=7^2\\ x=\pm7\)
\(e.\left(1,2\right)^3x^2=\left(1,2\right)^5\\ x^2=\dfrac{\left(1,2\right)^5}{\left(1,2\right)^3}\\ x^2=\left(1,2\right)^2\\ x=\pm1,2\\ f.\left(\dfrac{2}{3}x-\dfrac{1}{4}\right)^2=4\\ \left(\dfrac{2}{3}x-\dfrac{1}{4}\right)^2=2^2\\TH1:\dfrac{2}{3}x-\dfrac{1}{4}=2\\ \dfrac{2}{3}x=2+\dfrac{1}{4}=\dfrac{9}{4}\\ x=\dfrac{9}{4}:\dfrac{2}{3}=\dfrac{27}{8}\\ TH2:\dfrac{2}{3}x-\dfrac{1}{4}=-2\\ \dfrac{2}{3}x=-2+\dfrac{1}{4}=-\dfrac{7}{4}\\ x=\dfrac{-7}{4}:\dfrac{2}{3}=-\dfrac{21}{8}\\ g.\left(\dfrac{1}{6}x-3\right)^2=\dfrac{4}{9}\\ \left(\dfrac{1}{6}x-3\right)^2=\left(\dfrac{2}{3}\right)^2\\ TH1:\dfrac{1}{6}x-3=\dfrac{2}{3}\\ \dfrac{1}{6}x=\dfrac{2}{3}+3=\dfrac{11}{3}\\ x=\dfrac{11}{3}:\dfrac{1}{6}=22\\ TH2:\dfrac{1}{6}x-3=-\dfrac{2}{3}\\ \dfrac{1}{6}x=-\dfrac{2}{3}+3=\dfrac{7}{3}\\ x=\dfrac{7}{3}:\dfrac{1}{6}=14\)

\(a.\dfrac{1}{2}-3x=-\dfrac{2}{5}\\ 3x=\dfrac{1}{2}+\dfrac{2}{5}\\ 3x=\dfrac{9}{10}\\ x=\dfrac{9}{10}:3\\ x=\dfrac{3}{10}\\ b.-x+\dfrac{1}{2}=-\dfrac{5}{6}\\ x=\dfrac{1}{2}+\dfrac{5}{6}\\ x=\dfrac{4}{3}\\ c.x+\dfrac{3}{5}=\left(-\dfrac{2}{5}\right)^2\\ x+\dfrac{3}{5}=\dfrac{4}{25}\\ x=\dfrac{4}{25}-\dfrac{3}{5}\\ x=-\dfrac{11}{25}\\ d.\dfrac{3}{7}+\dfrac{1}{7}:x=\dfrac{3}{14}\\ \dfrac{1}{7}:x=\dfrac{3}{14}-\dfrac{3}{7}=-\dfrac{3}{14}\\ x=\dfrac{1}{7}:-\dfrac{3}{14}=-\dfrac{2}{3}\\ e.-\dfrac{1}{3}\left(\dfrac{1}{7}-x\right)=\dfrac{1}{21}\\ \dfrac{1}{7}-x=\dfrac{1}{21}:-\dfrac{1}{3}=-\dfrac{1}{7}\\ x=\dfrac{1}{7}+\dfrac{1}{7}=\dfrac{2}{7}\\ h.\dfrac{1}{4}-3x+\dfrac{3}{2}=-0,75\\ \dfrac{1}{4}-3x+\dfrac{3}{2}=-\dfrac{3}{4}\\ 3x=\dfrac{1}{4}+\dfrac{3}{2}+\dfrac{3}{4}=\dfrac{5}{2}\\ x=\dfrac{5}{2}:3\\ x=\dfrac{5}{6}\\ i.\dfrac{2}{7}-\left(\dfrac{2}{3}+2x\right)=\dfrac{5}{7}\\ \dfrac{2}{3}+2x=\dfrac{2}{7}-\dfrac{5}{7}=-\dfrac{3}{7}\\ 2x=-\dfrac{3}{7}-\dfrac{2}{3}=-\dfrac{23}{21}\\ x=\dfrac{-23}{21}:2=-\dfrac{23}{42}\)
a: \(\dfrac{1}{2}-3x=-\dfrac{2}{5}\)
=>\(3x=\dfrac{1}{2}+\dfrac{2}{5}=\dfrac{5}{10}+\dfrac{4}{10}=\dfrac{9}{10}\)
=>\(x=\dfrac{9}{10}:3=\dfrac{9}{30}=\dfrac{3}{10}\)
b: \(-x+\dfrac{1}{2}=-\dfrac{5}{6}\)
=>\(-x=-\dfrac{5}{6}-\dfrac{1}{2}=-\dfrac{5}{6}-\dfrac{3}{6}=-\dfrac{8}{6}=-\dfrac{4}{3}\)
=>\(x=\dfrac{4}{3}\)
c: \(x+\dfrac{3}{5}=\left(-\dfrac{2}{5}\right)^2\)
=>\(x+\dfrac{3}{5}=\dfrac{4}{25}\)
=>\(x=\dfrac{4}{25}-\dfrac{3}{5}=\dfrac{4}{25}-\dfrac{15}{25}=-\dfrac{11}{25}\)
d: \(\dfrac{3}{7}+\dfrac{1}{7}:x=\dfrac{3}{14}\)
=>\(\dfrac{1}{7}:x=\dfrac{3}{14}-\dfrac{3}{7}=-\dfrac{3}{14}\)
=>\(x=-\dfrac{1}{7}:\dfrac{3}{14}=-\dfrac{1}{7}\cdot\dfrac{14}{3}=-\dfrac{2}{3}\)
e: \(-\dfrac{1}{3}\left(\dfrac{1}{7}-x\right)=\dfrac{1}{21}\)
=>\(\dfrac{1}{7}-x=\dfrac{1}{21}:\dfrac{-1}{3}=\dfrac{-1}{21}\cdot3=-\dfrac{1}{7}\)
=>\(x=\dfrac{1}{7}+\dfrac{1}{7}=\dfrac{2}{7}\)
h: \(\dfrac{1}{4}-3x+\dfrac{3}{2}=-0,75\)
=>\(-3x+\dfrac{5}{4}=-\dfrac{3}{4}\)
=>\(-3x=-\dfrac{3}{4}-\dfrac{5}{4}=-\dfrac{8}{4}=-2\)
=>\(x=\dfrac{-2}{-3}=\dfrac{2}{3}\)
i: \(\dfrac{2}{7}-\left(\dfrac{2}{3}+2x\right)=\dfrac{5}{7}\)
=>\(2x+\dfrac{2}{3}=\dfrac{2}{7}-\dfrac{5}{7}=-\dfrac{3}{7}\)
=>\(2x=-\dfrac{3}{7}-\dfrac{2}{3}=-\dfrac{9}{21}-\dfrac{14}{21}=-\dfrac{23}{21}\)
=>\(x=-\dfrac{23}{21}:2=-\dfrac{23}{42}\)

\(a.\dfrac{3}{7}\cdot\dfrac{5}{8}+\dfrac{3}{7}\cdot\dfrac{11}{8}+\dfrac{11}{7}=\dfrac{3}{7}\cdot\left(\dfrac{5}{8}+\dfrac{11}{8}\right)+\dfrac{11}{7}=\dfrac{3}{7}\cdot2+\dfrac{11}{7}=\dfrac{6}{7}+\dfrac{11}{7}=\dfrac{17}{7}\\ b.\dfrac{3}{8}\cdot19\dfrac{1}{3}-\dfrac{3}{8}\cdot\left(33\dfrac{1}{3}\right)=\dfrac{3}{8}\cdot\left(19\dfrac{1}{3}-33\dfrac{1}{3}\right)=\dfrac{3}{8}\cdot-14=\dfrac{-21}{8}\\ c.\dfrac{1}{3}\cdot\dfrac{5}{4}+\dfrac{1}{3}\cdot\dfrac{7}{4}-2022^0=\dfrac{1}{3}\cdot\left(\dfrac{5}{4}+\dfrac{7}{4}\right)-1=\dfrac{1}{3}\cdot\dfrac{12}{4}-1=\dfrac{1}{3}\cdot3-1=1-1=0\\ d.\dfrac{5}{13}+\left(-\dfrac{5}{17}\right)+\dfrac{-21}{41}+\dfrac{8}{13}+\dfrac{-20}{41}=\left(\dfrac{5}{13}+\dfrac{8}{13}\right)+\left(-\dfrac{5}{17}\right)+\left(\dfrac{-21}{41}+\dfrac{-20}{41}\right)=1+\left(-\dfrac{5}{17}\right)-1=-\dfrac{5}{17}\)
\(e.\dfrac{27}{13}:\dfrac{9}{7}+\dfrac{12}{13}:\dfrac{9}{7}=\dfrac{27}{13}\cdot\dfrac{7}{9}+\dfrac{12}{13}\cdot\dfrac{7}{9}=\dfrac{7}{9}\cdot\left(\dfrac{27}{13}+\dfrac{12}{13}\right)=\dfrac{7}{9}\cdot\dfrac{39}{13}=\dfrac{7}{9}\cdot3=\dfrac{7}{3}\\ g.\dfrac{8}{15}\cdot-\dfrac{4}{9}+\dfrac{8}{15}:\dfrac{-9}{5}-3\dfrac{2}{5}=\dfrac{8}{15}\cdot\dfrac{-4}{9}+\dfrac{8}{15}\cdot\dfrac{-5}{9}-\dfrac{17}{5}=\dfrac{8}{15}\cdot\left(\dfrac{-4}{9}+\dfrac{-5}{9}\right)-\dfrac{17}{5}=-\dfrac{8}{15}-\dfrac{17}{5}=-\dfrac{59}{15}\\ h.\left(-\dfrac{2}{3}+\dfrac{3}{13}\right):\dfrac{7}{8}+\left(-\dfrac{1}{3}+\dfrac{10}{13}\right):\dfrac{7}{8}=\left(-\dfrac{2}{3}+\dfrac{3}{13}\right)\cdot\dfrac{8}{7}+\left(-\dfrac{1}{3}+\dfrac{10}{13}\right)\cdot\dfrac{8}{7}=\dfrac{8}{7}\cdot\left(-\dfrac{2}{3}+\dfrac{3}{13}-\dfrac{1}{3}+\dfrac{10}{3}\right)=\dfrac{8}{7}\cdot\left(-1+1\right)=\dfrac{8}{7}\cdot0=0\)

Ta có: ΔAHD vuông tại H
=>AD là cạnh huyền
=>AD>AH
mà AD=BC(ABCD là hình thang cân)
nên BC>AH
Ta có: KI là đường trung trực của AH
=>KI\(\perp\)AH và K là trung điểm của AH
Ta có: KI\(\perp\)AH
AH\(\perp\)HD
Do đó: KI//HD
=>\(\widehat{KIH}=\widehat{IHD}\)(1)
Xét ΔAHD có
K là trung điểm của AH
KI//HD
Do đó: I là trung điểm của AD
ΔAHD vuông tại H
mà HI là đường trung tuyến
nên IH=ID
=>ΔIHD cân tại I
=>\(\widehat{IHD}=\widehat{IDH}=\widehat{ADC}\left(2\right)\)
ABCD là hình thang cân
=>\(\widehat{ADC}=\widehat{BCD}\)(hai góc kề đáy CD)(3)
Từ (1),(2),(3) suy ra \(\widehat{HIK}=\widehat{BCD}\)

\(a.\left(\dfrac{1}{2}\right)^2-\dfrac{3}{8}:-\dfrac{9}{2}=\dfrac{1}{4}-\dfrac{3}{8}\cdot\dfrac{-2}{9}=\dfrac{1}{4}+\dfrac{1}{12}=\dfrac{4}{12}=\dfrac{1}{3}\)
\(b.\dfrac{1}{2}:\left(\dfrac{4}{5}-\dfrac{1}{2}\right)=\dfrac{1}{2}:\dfrac{4\cdot2-5}{10}=\dfrac{1}{2}:\dfrac{3}{10}=\dfrac{1}{2}\cdot\dfrac{10}{3}=\dfrac{5}{3}\)
\(c.\left(-\dfrac{1}{3}\right)^2:\dfrac{5}{9}+\left(-1\right)^3=\dfrac{1}{9}:\dfrac{5}{9}-1=\dfrac{1}{9}\cdot\dfrac{9}{5}-1=\dfrac{1}{5}-1=-\dfrac{4}{5}\)
\(d.\left(\dfrac{3}{5}\right)^2-\left(\dfrac{4}{5}-6\dfrac{1}{2}\right)=\dfrac{9}{25}-\dfrac{4}{5}+6\dfrac{1}{2}=\dfrac{9}{25}-\dfrac{20}{25}+\dfrac{13}{2}=\dfrac{-11}{25}+\dfrac{13}{2}=\dfrac{303}{50}\)
a) \(\left(\dfrac{1}{2}\right)^2-\dfrac{3}{8}:\dfrac{-9}{2}=\dfrac{1}{4}-\dfrac{3}{8}\times\dfrac{2}{-9}\\ =\dfrac{1}{4}-\left(-\dfrac{1}{12}\right)=\dfrac{3}{12}+\dfrac{1}{12}=\dfrac{4}{12}=\dfrac{1}{3}\)
b) \(\dfrac{1}{2}:\left(\dfrac{4}{5}-\dfrac{1}{2}\right)=\dfrac{1}{2}:\dfrac{3}{10}\\ =\dfrac{1}{2}\times\dfrac{10}{3}=\dfrac{5}{3}\)
c) \(\left(-\dfrac{1}{3}\right)^2:\dfrac{5}{9}+\left(-1\right)^3=\dfrac{1}{9}\times\dfrac{9}{5}-1=\dfrac{1}{5}-1\\ =-\dfrac{4}{5}\)

Bài 1
a: ĐKXĐ: \(n\ne4\)
Để A nguyên thì \(3n+9⋮n-4\)
=>\(3n-12+21⋮n-4\)
=>\(21⋮n-4\)
=>\(n-4\in\left\{1;-1;3;-3;7;-7;21;-21\right\}\)
=>\(n\in\left\{5;3;7;1;11;-3;25;-17\right\}\)
b: ĐKXĐ: n<>1/2
Để B nguyên thì \(6n+5⋮2n-1\)
=>\(6n-3+8⋮2n-1\)
=>\(8⋮2n-1\)
mà 2n-1 lẻ(do n nguyên)
nên \(2n-1\in\left\{1;-1\right\}\)
=>\(n\in\left\{1;0\right\}\)
Bài 2:
a: \(\left|x-\dfrac{1}{2}\right|>=0\forall x\)
=>\(-\dfrac{1}{2}\left|x-2\right|< =0\forall x\)
=>\(A=-\dfrac{1}{2}\left|x-2\right|+\dfrac{3}{2}< =\dfrac{3}{2}\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
b: \(\left|\dfrac{1}{2}-x\right|>=0\forall x\)
=>\(-2,3\left|\dfrac{1}{2}-x\right|< =0\forall x\)
=>\(D=-2,3\left|\dfrac{1}{2}-x\right|+2< =2\forall x\)
Dấu '=' xảy ra khi 1/2-x=0
=>x=1/2
Bài 1:
\(A=\dfrac{3n+9}{n-4}=\dfrac{3n-12}{n-4}+\dfrac{21}{n-4}=3+\dfrac{21}{n-4}\)
Để A nguyên thì \(\dfrac{21}{n-4}\) phải nguyên hay \(\left(n-4\right)\inƯ\left(21\right)=\left\{1;-1;3;-3;7;-7;21;-21\right\}\)
\(\Rightarrow n\in\left\{5;3;7;1;11;-3;25;-17\right\}\) (thoả mãn điều kiện)
Vậy...
\(B=\dfrac{6n+5}{2n-1}=\dfrac{6n-3}{2n-1}+\dfrac{8}{2n-1}=3+\dfrac{8}{2n-1}\)
Để B nguyên thì \(\dfrac{8}{2n-1}\) phải nguyên hay \(\left(2n-1\right)\inƯ\left(8\right)=\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
Mặt khác: Vì n nguyên nên 2n-1 là số lẻ
Do đó: \(\left(2n-1\right)\in\left\{1;-1\right\}\)
\(\Rightarrow n\in\left\{1;0\right\}\)
Vậy....
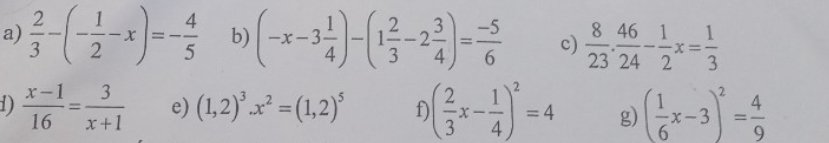

B5:
a) Thay x = 1 và y = 2 vào pt ta có:
\(m\cdot1+2-5=0\\ =>m-3=0\\ =>m=3\)
b) A(0;3) thuộc đường thẳng 4x - my - 6 = 0
=> Thay x = 0 và y = 3 vào đường thẳng ta có:
\(4\cdot0-m\cdot3-6=0\\ =>0-3m-6=0\\=> -3m-6=0\\ =>-3m=6\\ =>m=\dfrac{6}{-3}=-2\)
B11:
Ta có:
\(\left\{{}\begin{matrix}2x+3y=7\\x-3y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=6\\x-3y=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{6}{3}=2\\2-3y=-1\end{matrix}\right. \Leftrightarrow\left\{{}\begin{matrix}x=2\\3y=2+1=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{3}{3}=1\end{matrix}\right.\)
=> Cặp (2;1) là nghiệm của hpt
B12:
Ta có
\(\left\{{}\begin{matrix}4x+5y=3\\x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+5y=3\\4x-12y=20\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}17y=-17\\x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-17}{17}=-1\\x+3=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=5-3=2\end{matrix}\right.\)
=> Cặp (2;-1) là nghiệm của hpt