1. Tim GTLN của biểu thức A= \(\frac{-9x+\sqrt{x}-1}{\sqrt{x}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\sqrt{x}+2=\frac{1}{2}\)
\(\Leftrightarrow\sqrt{x}=\frac{-3}{2}\)(Vô lý)
Vậy phương trình trên vô nghiệm
b) \(-2\sqrt{x}+3=0\)
\(\Leftrightarrow-2\sqrt{x}=-3\)
\(\Leftrightarrow\sqrt{x}=\frac{3}{2}\)
\(\Leftrightarrow\sqrt{x}=\sqrt{\left(\frac{3}{2}\right)^2}\)
\(\Leftrightarrow x=\left(\frac{3}{2}\right)^2\)
\(\Leftrightarrow x=\frac{9}{4}\)
Vậy nghiệm của phương trình là: \(x=\left\{\frac{9}{4}\right\}\)
c) \(\frac{\sqrt{2x+4}}{2}=3\)
\(\Leftrightarrow\sqrt{2x+4}=6\)
\(\Leftrightarrow\sqrt{2x+4}=\sqrt{6^2}\)
\(\Leftrightarrow2x+4=36\)
\(\Leftrightarrow x=16\)
Vậy nghiệm của phương trình là: \(x=\left\{16\right\}\)

Ta có: \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\ge\left(a+b\right)\left(2ab-ab\right)=ab\left(a+b\right)\)
\(\Rightarrow a^3+b^3+abc\ge ab\left(a+b+c\right)\)
\(\Rightarrow\frac{1}{a^3+b^3+abc}\le\frac{1}{ab\left(a+b+c\right)}\)
Tương tự: ...
\(\Rightarrow VT\le\frac{1}{a+b+c}\cdot\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\right)=\frac{1}{a+b+c}\cdot\frac{a+b+c}{abc}=\frac{1}{abc}\)
Dấu "=" xảy ra khi: a = b = c

Điều kiện xác định : \(1\ge a\ge0\)
a, Ta có : \(\frac{\sqrt{1+a}}{\sqrt{1+a}-\sqrt{1-a}}+\frac{1-a}{\sqrt{1-a^2}-1+a}=\frac{\sqrt{1+a}+\sqrt{1-a}}{\sqrt{1+a}-\sqrt{1-a}}=\frac{1+\sqrt{1-a^2}}{a}\)
\(\sqrt{\frac{1}{a^2}-1}-\frac{1}{a}=\sqrt{\frac{1-a^2}{a^2}}-\frac{1}{a}=\frac{\sqrt{1-a^2}-1}{a}\)
\(\sqrt{a^2-2a+1}=\sqrt{\left(a-1\right)^2}=a-1\)
Suy ra \(Q=\frac{1+\sqrt{1-a^2}}{a}.\frac{\sqrt{1-a^2}-1}{a}.\left(a-1\right)=\frac{1-a^2-1}{a^2}.\left(a-1\right)=-1.\left(a-1\right)=1-a\)
b, Xét hiệu \(Q^3-Q=-2a+3a^2-a^3=-a\left(a^2-3a+2\right)=a\left(a-1\right)\left(2-a\right)\):vv
phải xét th a = 1 với a khác 1 nhé :)
gợi ý nè : a = 1 thì = nhau mà a khác 1 thì q^3 > q nhé
Tự làm 1 xíu nhé

a) \(x^2=\frac{1}{15}\)
\(\Leftrightarrow\sqrt{x^2}=\sqrt{\frac{1}{15}}\)
\(\Leftrightarrow\left|x\right|=\frac{1}{\sqrt{15}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{\sqrt{15}}\\x=-\frac{1}{\sqrt{15}}\end{cases}}\)
Vậy \(x=\left\{\frac{1}{\sqrt{15}};-\frac{1}{\sqrt{15}}\right\}\)
b) \(\sqrt{x}-3=\frac{1}{3}\)
\(\Leftrightarrow\sqrt{x}=\frac{10}{3}\)
\(\Leftrightarrow\sqrt{x}=\sqrt{\left(\frac{10}{3}\right)^2}\)
\(\Leftrightarrow x=\left(\frac{10}{3}\right)^2\)
\(\Leftrightarrow x=\frac{100}{9}\)
Vậy \(x=\left\{\frac{100}{9}\right\}\)

a,Vì ABCD là hình chữ nhật => BC = AD = 15 cm
Xét tam giác ABD vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác ABD
\(BD^2=AB^2+AD^2=64+225=289\Rightarrow BD=17\)cm
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AD^2}\Rightarrow\frac{1}{AH^2}=\frac{1}{64}+\frac{1}{225}=\frac{225+64}{64.225}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{289}{14400}\Leftrightarrow AH^2=\frac{14400}{289}\Leftrightarrow AH=\frac{120}{17}\)
b, Xét tam giác AHB vuông tại H đường cao HI
\(AH^2=IA.AB\)( hệ thức lượng ) (1)
Xét tam giác ABD vuông tại A đường cao AH
\(AH^2=DH.BH\)( hệ thức lượng ) (2)
Từ (1) ; (2) suy ra \(IA.AB=DH.BH\)( đpcm )

đk: \(\orbr{\begin{cases}a\ge b\\a\le-b\end{cases}\left(b\ge0\right)}\) và a,b không đồng thời bằng 0
\(Q=\frac{a}{\sqrt{a^2-b^2}}-\left(1+\frac{a}{\sqrt{a^2-b^2}}\right)\div\frac{b}{a-\sqrt{a^2-b^2}}\)
\(Q=\frac{a}{\sqrt{a^2-b^2}}-\frac{a+\sqrt{a^2-b^2}}{\sqrt{a^2-b^2}}\cdot\frac{a-\sqrt{a^2-b^2}}{b}\)
\(Q=\frac{a}{\sqrt{a^2-b^2}}-\frac{a^2-\left(a^2-b^2\right)}{b\sqrt{a^2-b^2}}\)
\(Q=\frac{a}{\sqrt{a^2-b^2}}-\frac{b^2}{b\sqrt{a^2-b^2}}\)
\(Q=\frac{a}{\sqrt{a^2-b^2}}-\frac{b}{\sqrt{a^2-b^2}}\)
\(Q=\frac{a-b}{\sqrt{a^2-b^2}}\)

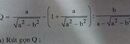

\(A=\frac{-9x+\sqrt{x}-1}{\sqrt{x}}=1-\left(9\sqrt{x}+\frac{1}{\sqrt{x}}\right)\le1-2\sqrt{9\sqrt{x}.\frac{1}{\sqrt{x}}}=1-2.3=-5\)
Dấu \(=\)khi \(9\sqrt{x}=\frac{1}{\sqrt{x}}\Leftrightarrow x=\frac{1}{9}\)
Vậy \(maxA=-5\).