Bán kính đáy là: \(1,7:2=0,85\left(m\right)\)

Thể tích bồn là: \(V=\pi R^2h=\pi.0,85^2.4,8\approx10,9\left(m^3\right)\)

Bồn chứa được nhiều nhất là: \(10,9\times90\%=9,8\left(m^3\right)\)

Để tính dung tích của bồn chứa LPG, ta sử dụng công thức:

\[ V = \pi \times r^2 \times h \]

Trong đó:
- \( V \) là dung tích của bồn chứa LPG,
- \( r \) là bán kính đáy của hình trụ (\( r = \frac{d}{2} \)),
- \( h \) là chiều cao của hình trụ.

Với \( d \) là đường kính đáy của hình trụ, ta có:
\[ r = \frac{1.7}{2} = 0.85 \, \text{m} \]

Vậy \( r = 0.85 \, \text{m} \).

\[ h = 4.8 \, \text{m} \]

Dung tích bồn chứa LPG là:
\[ V = \pi \times (0.85)^2 \times 4.8 \]
\[ V = \pi \times 0.7225 \times 4.8 \]
\[ V \approx 10.89 \pi \, \text{m}^3 \]

Theo quy chuẩn kỹ thuật, lượng LPG không được vượt quá 90% dung tích bồn chứa. Vậy dung tích tối đa của LPG trong bồn là:
\[ 0.9 \times 10.89 \pi \approx 9.801 \pi \, \text{m}^3 \]

Để chuyển sang diện tích, chúng ta sử dụng công thức:
\[ \text{Diện tích} = \frac{\text{Dung tích}}{\text{Chiều cao bồn}} \]

\[ \text{Diện tích} = \frac{9.801 \pi}{4.8} \approx 6.13 \, \text{m}^2 \]

Vậy bồn có thể chứa nhiều nhất khoảng \(6.13 \, \text{m}^2\) LPG.

Gọi số tuổi của An là x, số tuổi của mẹ An là y (x;y là số nguyên dương)

Do 3 lần tuổi An ít hơn tuổi mẹ An là 4 tuổi nên ta có:

\(y-3x=4\) (1)

Do 4 lần tuổi An nhiều hơn mẹ An 10 tuổi nên ta có:

\(4x-y=10\) (2)

Từ (1);(2) ta có hệ:

\(\left\{{}\begin{matrix}-3x+y=4\\4x-y=10\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=14\\y=46\end{matrix}\right.\)

Gọi \(x\) là số tuổi của An và \(y\) là số tuổi của mẹ An.

Theo đề bài, ta có hệ phương trình sau:

1. Ba lần tuổi của An nhỏ hơn tuổi của mẹ An là 4 tuổi:
\[3x = y - 4\]

2. Bốn lần tuổi của An lại lớn hơn tuổi của mẹ An là 10 tuổi:
\[4x = y + 10\]

Giải hệ phương trình này để tìm \(x\) và \(y\):

Từ phương trình 1, ta có \(y = 3x + 4\).

Thay \(y\) vào phương trình 2, ta được:
\[4x = (3x + 4) + 10\]
\[4x = 3x + 14\]
\[x = 14\]

Thay \(x = 14\) vào phương trình 1, ta được:
\[3(14) = y - 4\]
\[42 = y - 4\]
\[y = 46\]

Vậy, số tuổi của mẹ An là 46 tuổi và số tuổi của An là 14 tuổi.

Do \(ac< 0\) (đối với cả 2 pt) nên 2 pt đã cho đều có 2 nghiệm pb trái dấu

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+2\\x_1x_2=-\dfrac{1}{2}\end{matrix}\right.\) và \(\left\{{}\begin{matrix}x_3+x_4=-\left(m+2\right)\\x_3x_4=-2\end{matrix}\right.\)

\(\Rightarrow x_1x_2+x_3x_4=-\dfrac{1}{2}-2=-\dfrac{5}{2}\)

\(\Rightarrow x_1x_3+x_2x_4=x_1x_2+x_3x_4\)

\(\Rightarrow x_1\left(x_3-x_2\right)-x_4\left(x_3-x_2\right)=0\)

\(\Rightarrow\left(x_1-x_4\right)\left(x_3-x_2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x_1=x_4\\x_2=x_3\end{matrix}\right.\)

\(\Rightarrow\) Hai pt đã cho có ít nhất 1 nghiệm chung. Gọi nghiệm chung đó là \(x_0\)

\(\Rightarrow\left\{{}\begin{matrix}2x_0^2-\left(m+2\right)x_0-1=0\\x_0^2+\left(m+2\right)x_0-2=0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}2x_0^2-\left(m+2\right)x_0-1=0\left(1\right)\\2x_0^2+2\left(m+2\right)x_0-4=0\left(2\right)\end{matrix}\right.\)

Trừ vế (2) cho (1)

\(\Rightarrow3\left(m+2\right)x_0-3=0\Rightarrow x_0=\dfrac{1}{m+2}\) (với \(x\ne-2\))

Thế vào (1)

\(\Rightarrow\dfrac{2}{\left(m+2\right)^2}-2=0\Rightarrow\left(m+2\right)^2=1\)

\(\Rightarrow\left[{}\begin{matrix}m=-1\\m=-3\end{matrix}\right.\)

Gọi số sản phẩm ban đầu nhóm công nhân dự định làm trong 1 ngày là x(sản phẩm)

(ĐK: \(x\in Z^+\))

Số ngày ban đầu dự kiến sẽ hoàn thành là \(\dfrac{500}{x}\left(ngày\right)\)

Sau 4 ngày đầu thì số sản phẩm nhóm công nhân làm được là 4x(sản phẩm)

=>Số sản phẩm còn lại cần làm là 500-4x(sản phẩm)

Thời gian hoàn thành phần còn lại là: \(\dfrac{500-4x}{x+10}\left(ngày\right)\)

Theo đề, ta có phương trình:

\(\dfrac{500-4x}{x+10}+4=\dfrac{500}{x}-1\)

=>\(\dfrac{500-4x}{x+10}+5=\dfrac{500}{x}\)

=>\(\dfrac{500-4x+5x+50}{x+10}=\dfrac{500}{x}\)

=>\(\dfrac{x+550}{x+10}=\dfrac{500}{x}\)

=>\(x\left(x+550\right)=500\left(x+10\right)\)

=>\(x^2+550x-500x-5000=0\)

=>\(x^2+50x-5000=0\)

=>(x+100)(x-50)=0

=>\(\left[{}\begin{matrix}x=-100\left(loại\right)\\x=50\left(nhận\right)\end{matrix}\right.\)

Vậy: Số sản phẩm dự kiến làm trong 1 ngày là 50 sản phẩm

a) ∆' = (-m)² - (2m - 1)

= m² - 2m + 1

= (m - 1)² ≥ 0 với mọi m ∈ R

Vậy phương trình luôn có hai nghiệm với mọi m ∈ R

b) Theo hệ thức Vi-ét, ta có:

x₁ + x₂ = 2m

x₁x₂ = 2m - 1

(x₁ + x₂)² - 4x₁x₂ = -4

(2m)² - 4(2m - 1) = -4

4m² - 8m + 4 + 4 = 0

4m² - 8m + 8 = 0 (*)

∆' = (-4)² - 4.8 = -16 < 0

⇒ (*) vô nghiệm

Vậy không tìm được m thỏa mãn (x₁ + x₂)² - 4x₁x₂ = -4

                          Giải

Gọi số ngày mà tổ đó phải hoàn thành theo kế hoạch là: \(x\) (ngày)

Điều kiện: \(x\) \(\in\) N

Số ngày thực tế đội đó hoàn thành là: \(x\) - 2 (ngày)

Số áo mỗi ngày đội đó làm được theo kế hoạch là: \(\dfrac{1200}{x}\) (chiếc áo)

Số áo mỗi ngày mà đội đó làm được trên thực tế là: \(\dfrac{1200}{x-2}\) (chiếc áo)

Theo bài ra ta có phương trình: 

               \(\dfrac{1200}{x-2}\) - \(\dfrac{1200}{x}\) = 20

                \(\dfrac{60}{x-2}\) - \(\dfrac{60}{x}\) = 1

                  60\(x\) - 60\(x\) + 120 = \(x^2\) - 2\(x\) 

                  \(x^2\) - 2\(x\) + 1 = 121

                   (\(x\) - 1)² = 11²

                \(\left[{}\begin{matrix}x-1=11\\x-1=-11\end{matrix}\right.\)

                \(\left[{}\begin{matrix}x=12\\x=-10\end{matrix}\right.\)

Vì \(x\) > 0 nên \(x\) = 12

Kêt luận số ngày mà đội đó phải hoàn thành theo kế hoạch là 12 ngày. 

Gọi thời gian tổ may xong áo theo kế hoạch là \(x(\text{ngày};x\in \mathbb{N}^*)\)

Theo kế hoạch thì mỗi ngày tổ may được: \(\dfrac{1200}{x}\) (chiếc áo)

Thời gian tổ may xong trên thực tế là: \(x-2\) (ngày)

Trên thực tế thì mỗi ngày tổ may được: \(\dfrac{1200}{x-2}\) (chiếc áo)

Do cải tiến kỹ thuật nên mỗi ngày tổ may thêm được 20 chiếc áo, khi đó ta có pt:

\(\dfrac{1200}{x}+20=\dfrac{1200}{x-2}\)

\(\Leftrightarrow1200\cdot\left(\dfrac{1}{x-2}-\dfrac{1}{x}\right)=20\)

\(\Leftrightarrow\dfrac{x-\left(x-2\right)}{x\left(x-2\right)}=\dfrac{20}{1200}\)

\(\Leftrightarrow\dfrac{2}{x^2-2x}=\dfrac{1}{60}\)

\(\Rightarrow x^2-2x=120\)

\(\Leftrightarrow x^2-2x-120=0\)

\(\Leftrightarrow\left(x-1\right)^2-121=0\)

\(\Leftrightarrow\left(x-12\right)\left(x+10\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-12=0\\x+10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=12\left(tm\right)\\x=-10\left(ktm\right)\end{matrix}\right.\)

Vậy theo kế hoạch tổ phải may số áo trên trong 12 ngày.

                          Giải

Gọi số ngày mà tổ đó phải hoàn thành theo kế hoạch là: \(x\) (ngày)

Điều kiện: \(x\) \(\in\) N

Số ngày thực tế đội đó hoàn thành là: \(x\) - 2 (ngày)

Số áo mỗi ngày đội đó làm được theo kế hoạch là: \(\dfrac{1200}{x}\) (chiếc áo)

Số áo mỗi ngày mà đội đó làm được trên thực tế là: \(\dfrac{1200}{x-2}\) (chiếc áo)

Theo bài ra ta có phương trình: 

               \(\dfrac{1200}{x-2}\) - \(\dfrac{1200}{x}\) = 20

                \(\dfrac{60}{x-2}\) - \(\dfrac{60}{x}\) = 1

                  60\(x\) - 60\(x\) + 120 = \(x^2\) - 2\(x\) 

                  \(x^2\) - 2\(x\) + 1 = 121

                   (\(x\) - 1)² = 11²

                \(\left[{}\begin{matrix}x-1=11\\x-1=-11\end{matrix}\right.\)

                \(\left[{}\begin{matrix}x=12\\x=-10\end{matrix}\right.\)

Vì \(x\) > 0 nên \(x\) = 12

Kêt luận số ngày mà đội đó phải hoàn thành theo kế hoạch là 12 ngày. 

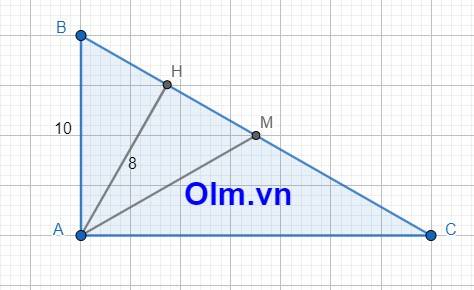
        Bài 1:

Theo pytago ta có: HB² + AH² = AB² 

          ⇒ HB² = AB² - AH² 

              HB² = 10² -  8² = 36 

              HB = \(\sqrt{36}\) = 6 (cm)

Xét tam giác ABC  và tam giác HBA có:

            \(\widehat{BAC}\) = \(\widehat{BHA}\) = 90⁰

            \(\widehat{ABC}\) = \(\widehat{HBA}\)

⇒ \(\Delta\) ABC \(\sim\) \(\Delta\) HBA (g - g)

⇒ \(\dfrac{AB}{HB}\) = \(\dfrac{BC}{BA}\)

      BC = \(\dfrac{AB}{HB}\) \(\times\) AB 

      BC = \(\dfrac{10.10}{6}\) = \(\dfrac{50}{3}\) (cm)

      S_ABC = \(\dfrac{1}{2}\)BC \(\times\)  AH  = \(\dfrac{1}{2}\) \(\times\) \(\dfrac{50}{3}\) \(\times\) 8 = \(\dfrac{200}{3}\) (cm²)

Vì M là trung điểm của tam giác ABC nên 

   S_ABM  = \(\dfrac{1}{2}\) S_ABC (hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và BM = \(\dfrac{1}{2}\) BC)

   S_ABM = \(\dfrac{200}{3}\).\(\dfrac{1}{2}\) = \(\dfrac{100}{3}\) (cm²)

  S_AHB = \(\dfrac{1}{2}\)AH.HB = \(\dfrac{8.6}{2}\) = 24 (cm²)

S_AHB + S_AHM = S_ABM

 ⇒ S_AHM = S_ABM - S_AHB 

    S_AHM = \(\dfrac{100}{3}\) - 24 = \(\dfrac{28}{3}\) (cm²)

Kết luận: BC dài \(\dfrac{50}{3}\) cm; Diện tích tam giác AHM là \(\dfrac{28}{3}\) cm²

dễ mà

Giải:

Gọi số phần quà ban đầu là n, từ để bài ta có phương trình:

(n+5)(n-6) = (n+10)(n-10)

<=> n= 70

=> Tổng số hộp sữa= (n=10)(n-10)= 80 x 60  =4800 hộp