chào nhé

Gọi $BF$ cắt $DC$ tại $K$, $BE$ cắt $DC$ tại $I$, và $EF$ cắt $AB$ tại $G$.

$\Delta FAB$ có $DK$ // $AB$ suy ra ����=����ABDK​=FAFD​ (1)

$\Delta FAG$ có $DH$ // $AG$ suy ra ����=����AGDH​=FAFD​ (2)

Từ (1) và (2) suy ra ����=����ABDK​=AGDH​ hay ����=����DHDK​=AGAB​ (*)

Tương tự $\Delta EIC$ có $AB$ // $IC$ suy ra ����=����ABIC​=EAEC​ (3)

$\Delta EHC$ có $HC$ // $AB$ suy ra ����=����AGHC​=EAEC​ (4)

Từ (3) và (4) ta có ����=����ABIC​=AGHC​ hay ����=����HCIC​=AGAB​ (**)

Từ (*) và (**) ta có ����=����DHDK​=HCIC​.

Mà $DH=HC$ (gt) suy ra $DK=IC$

Mặt khác $BD=BC$ (gt) nên $\Delta BDC$ cân

Suy ra ���^=���^BDK=BCI

Vậy $\Delta BDK=\Delta BCI$ (c.g.c)

Suy ra ���^=���^DBK=CBI.

a) $\Delta ABE$ có $AM$ // $DG$ suy ra ����=����EGAE​=EDEB​ (1)

$\Delta ADE$ có $AD$ // $BK$ suy ra ����=����EDEB​=EAEK​ (2)

Từ (1) và (2) ta có ����=����EGAE​=EAEK​ nên ��2=��.��AE2=EK.EG.

b) Từ 1��=1��+1��AE1​=AK1​+AG1​ suy ra ����+����=1AKAE​+AGAE​=1

$\Delta ADE$ có $AD$ // $BC$ suy ra ����=����EKAE​=EBED​

     ����+��=����+��AE+EKAE​=ED+EBED​

     ����=����AKAE​=DBED​ (3)

Tương tự $\Delta AEB$ có $AB$ // $DG$ suy ra ����=����EGAE​=EDBE​

     ����+��=����+��AE+EGAE​=BE+EDBE​

     ����=����AGAE​=BDBE​ (4)

Khi đó ����+����=����+����=1AKAE​+AGAE​=BDED​+BDBE​=1.

c) Ta có ����=����KCBK​=CGAB​ suy ra ��=��.����BK=CGKC.AB​ và ����=����ADKC​=DGCG​.

Suy ra ��=��.����DG=KCAD.CG​

Nhân theo vế ta được $BK.DG=AB.AD$ không đổi.

a) $\Delta ABE$ có $AM$ // $DG$ suy ra ����=����EGAE​=EDEB​ (1)

$\Delta ADE$ có $AD$ // $BK$ suy ra ����=����EDEB​=EAEK​ (2)

Từ (1) và (2) ta có ����=����EGAE​=EAEK​ nên ��2=��.��AE2=EK.EG.

b) Từ 1��=1��+1��AE1​=AK1​+AG1​ suy ra ����+����=1AKAE​+AGAE​=1

$\Delta ADE$ có $AD$ // $BC$ suy ra ����=����EKAE​=EBED​

     ����+��=����+��AE+EKAE​=ED+EBED​

     ����=����AKAE​=DBED​ (3)

Tương tự $\Delta AEB$ có $AB$ // $DG$ suy ra ����=����EGAE​=EDBE​

     ����+��=����+��AE+EGAE​=BE+EDBE​

     ����=����AGAE​=BDBE​ (4)

Khi đó ����+����=����+����=1AKAE​+AGAE​=BDED​+BDBE​=1.

c) Ta có ����=����KCBK​=CGAB​ suy ra ��=��.����BK=CGKC.AB​ và ����=����ADKC​=DGCG​.

Suy ra ��=��.����DG=KCAD.CG​

Nhân theo vế ta được $BK.DG=AB.AD$ không đổi.

a) $\Delta ABE$ có $AM$ // $DG$ suy ra ����=����EGAE​=EDEB​ (1)

$\Delta ADE$ có $AD$ // $BK$ suy ra ����=����EDEB​=EAEK​ (2)

Từ (1) và (2) ta có ����=����EGAE​=EAEK​ nên ��2=��.��AE2=EK.EG.

b) Từ 1��=1��+1��AE1​=AK1​+AG1​ suy ra ����+����=1AKAE​+AGAE​=1

$\Delta ADE$ có $AD$ // $BC$ suy ra ����=����EKAE​=EBED​

     ����+��=����+��AE+EKAE​=ED+EBED​

     ����=����AKAE​=DBED​ (3)

Tương tự $\Delta AEB$ có $AB$ // $DG$ suy ra ����=����EGAE​=EDBE​

     ����+��=����+��AE+EGAE​=BE+EDBE​

     ����=����AGAE​=BDBE​ (4)

Khi đó ����+����=����+����=1AKAE​+AGAE​=BDED​+BDBE​=1.

c) Ta có ����=����KCBK​=CGAB​ suy ra ��=��.����BK=CGKC.AB​ và ����=����ADKC​=DGCG​.

Suy ra ��=��.����DG=KCAD.CG​

Nhân theo vế ta được $BK.DG=AB.AD$ không đổi.

a) $\Delta ABE$ có $AM$ // $DG$ suy ra ����=����EGAE​=EDEB​ (1)

$\Delta ADE$ có $AD$ // $BK$ suy ra ����=����EDEB​=EAEK​ (2)

Từ (1) và (2) ta có ����=����EGAE​=EAEK​ nên ��2=��.��AE2=EK.EG.

b) Từ 1��=1��+1��AE1​=AK1​+AG1​ suy ra ����+����=1AKAE​+AGAE​=1

$\Delta ADE$ có $AD$ // $BC$ suy ra ����=����EKAE​=EBED​

     ����+��=����+��AE+EKAE​=ED+EBED​

     ����=����AKAE​=DBED​ (3)

Tương tự $\Delta AEB$ có $AB$ // $DG$ suy ra ����=����EGAE​=EDBE​

     ����+��=����+��AE+EGAE​=BE+EDBE​

     ����=����AGAE​=BDBE​ (4)

Khi đó ����+����=����+����=1AKAE​+AGAE​=BDED​+BDBE​=1.

c) Ta có ����=����KCBK​=CGAB​ suy ra ��=��.����BK=CGKC.AB​ và ����=����ADKC​=DGCG​.

Suy ra ��=��.����DG=KCAD.CG​

Nhân theo vế ta được $BK.DG=AB.AD$ không đổi.

Qua $A$ vẽ đường thẳng song song với $BC$ cắt ��′BB′ tại $D$ và cắt ��′CC′ tại $E$.

Khi đó 

$\Delta AME$ có $AE$ // �′�A′C suy ra ���′�=���′�A′MAM​=A′CAE​ (1)

$\Delta AMD$ có $AD$ // �′�A′B suy ra ���′�=���′�A′MAM​=A′BAD​ (2)

Từ (1) và (2) ta có ���′�=���′�=���′�=��+���′�+�′�=����A′MAM​=A′CAE​=A′BAD​=A′C+A′BAD+AE​=BCDE​ (*)

Chứng minh tương tự ta cũng có:

Δ��′�ΔAB′D có $AD$ // $BC$ suy ra ��′�′�=����B′CAB′​=BCAD​ (3)

Δ��′�ΔAC′E có $AE$ // $BC$ suy ra ��′�′�=����C′BAC′​=BCAE​ (4)

Từ (3) và (4) ta có ��′�′�+��′��′=����+����=����B′CAB′​+BC′AC′​=BCAD​+BCAE​=BCDE​ (**)

Từ (*) và (**) ta có ���′�=����=��′�′�+��′��′A′MAM​=BCDE​=B′CAB′​+BC′AC′​ (đpcm).

Qua $A$ vẽ đường thẳng song song với $BC$ cắt ��′BB′ tại $D$ và cắt ��′CC′ tại $E$.

Khi đó 

$\Delta AME$ có $AE$ // �′�A′C suy ra ���′�=���′�A′MAM​=A′CAE​ (1)

$\Delta AMD$ có $AD$ // �′�A′B suy ra ���′�=���′�A′MAM​=A′BAD​ (2)

Từ (1) và (2) ta có ���′�=���′�=���′�=��+���′�+�′�=����A′MAM​=A′CAE​=A′BAD​=A′C+A′BAD+AE​=BCDE​ (*)

Chứng minh tương tự ta cũng có:

Δ��′�ΔAB′D có $AD$ // $BC$ suy ra ��′�′�=����B′CAB′​=BCAD​ (3)

Δ��′�ΔAC′E có $AE$ // $BC$ suy ra ��′�′�=����C′BAC′​=BCAE​ (4)

Từ (3) và (4) ta có ��′�′�+��′��′=����+����=����B′CAB′​+BC′AC′​=BCAD​+BCAE​=BCDE​ (**)

Từ (*) và (**) ta có ���′�=����=��′�′�+��′��′A′MAM​=BCDE​=B′CAB′​+BC′AC′​ (đpcm).

22. to get - driving

23. to seeing

24. talking

25. to arrive

26. serviced

27. made

28. to smoke

29. prepare

30. to repaired

31. broken

32. stolen

22 , When British people go abroad, it takes them several day __to get _ (get) used to __driving_ (drive) on the right-hand side of the road.

23)        I’m looking forward __to seeing__ (see) you again soon .

24)        Whenever we meet ,we stop _to talk__ (talk) .

25)        I don’t like being the first person _to arrive__ (arrive) at a party.

26)        You should have your car __serviced_ (service) regularly .

27)        I lost my key . I’ll have to get another key __made_ (make).

28)        He does not allow us _to smoke__ (smoke) in his house.

29)        The manager had his secretary __prepare__ (prepare) the report.

30)        I’m going to get Harry _to repair__ (repair) my car.

31)        George had his nose ___broken_ (break) in a fight.(đánh nhau)

32)        We had all our money __stolen__ (steal) while we were on holiday

\(\Leftrightarrow x^4-4x^3+12x^2-32x+32=\left(y-5\right)^2\)

\(\Leftrightarrow\left(x-2\right)^2\left(x^2+8\right)=\left(y-5\right)^2\)

- Với \(x=2\Rightarrow y=5\)

- Với \(x\ne2\Rightarrow x-2\) là ước của \(y-5\) 

Đặt \(y-5=n\left(x-2\right)\)

\(\Rightarrow\left(x-2\right)^2\left(x^2+8\right)=n^2\left(x-2\right)^2\)

\(\Rightarrow x^2+8=n^2\)

\(\Rightarrow\left(n-x\right)\left(n+x\right)=8\)

\(\Rightarrow\left[{}\begin{matrix}x=1;n=-3\Rightarrow y=8\\x=-1;n=-3\Rightarrow y=14\\x=1;n=3\Rightarrow y=2\\x=-1;n=3\Rightarrow y=-4\end{matrix}\right.\) 

Câu 1
\(a)PTHH:Mg+2HCl\rightarrow MgCl_2+H_2\\ b)200ml=0,2l\\ n_{HCl}=0,2.1=0,2mol\\ n_{H_2}=n_{MgCl_2}=\dfrac{1}{2}n_{H_2}=\dfrac{1}{2}\cdot0,2=0,1mol\\ V_{H_2}=0,1.24,79=2,479l\\ c)C_{M_{MgCl_2}}=\dfrac{0,1}{0,2}=0,5M\)

Câu 2
\(a)PTHH:Mg+2HCl\rightarrow MgCl_2+H_2\\ b)n_{Mg}=\dfrac{1,2}{24}=0,05mol\\ n_{H_2}=n_{MgCl_2}=n_{Mg}=0,05mol\\ V_{H_2}=0,05.24,79=1,2395l\\ c)n_{HCl}=2n_{Mg}=2.0,05=0,1mol\\ V_{ddHCl}=\dfrac{0,1}{2}=0,05l\\ d)C_{M_{MgCl_2}}=\dfrac{0,05}{0,05}=1M\)

1. Smartphones can be expensive because they come with many features.

=> Smartphones come with many features, so they can be expensive

2. Smartwatches can track your heart rate. They can also receive messages.

=> Smartwatches not only can track your heart rate, but also can receive messages

3. I enjoy taking photos with my phone, but the storage gets full quickly.

=> Although I enjoy taking photos with my phone, the storage gets full quickly.

4. Tablets are lightweight, so they are easy to carry in a bag.

=> Because tablets are lightweight, they are easy to carry in a bag.

5. I use noise-canceling headphones so that I can focus better in a noisy environment.

=> Because of using noise-canceling headphones, I can focus better in a noisy environment.

1 so

2 but

3 so

4 so

5 as

6 However

7 Therefore

1.so

2.but

3.and

4.yet

5.because

6.but

7.so

Bài 10

a; Giao của d1 với trục ox là điểm có hoành độ thỏa mãn

     \(x\) - 3 = 0 ⇒ \(x\) = 3

Giao của d1 với trục oy là điểm có tung độ thỏa mãn y = 0 - 3 = -3

Giao của d2 với trục ox là điểm có hoành độ thỏa mãn 

     3 - \(x\) = 0 ⇒ \(x\) = 3

Giao của d2 với trục oy là điểm có tung độ thỏa mãn y = 3 - 0 = 3

Ta có đồ thị d1 và d2 như hình dưới 

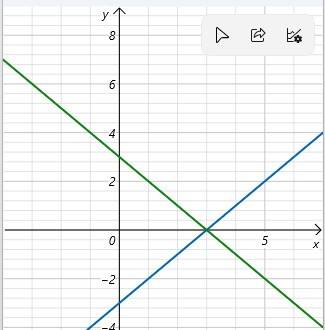
b; Giao của d1 và d2 là điểm có phương trình hoành độ thỏa mãn

\(x\) - 3 = 3 - \(x\)

2\(x\) = 6 

\(x\) = 6 : 2

\(x\) = 3; ⇒ y = 3- 3  =0 

Vậy giao của d1 và d2 là A(3;0)

Bài 9:

Giao của d1 với trục ox là điểm có hoành độ thỏa mãn 

              2\(x\) - 3  = 0 ⇒ \(x\) = \(\dfrac{3}{2}\)

Giao của d1 với trục oy là điểm có tung độ thỏa mãn

            y = 2.0 - 3  = - 3

Giao của d2 với trục ox là điểm có hoành độ thỏa mãn 

         -3 - \(x\) = 0 ⇒ \(x\) = 0

  Giao của d2 với trục oy là điểm có tung độ thỏa mãn

        y = -3 - 0 = -3

Ta có đồ thị như hình dưới đây

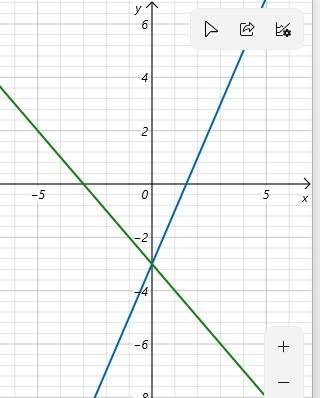
Giao của d1 và d2 là điểm có hoành độ thỏa mãn phương trình 

       2\(x\) - 3 = -3 - \(x\)

      2\(x\) + \(x\) = 0 

          3\(x\) =0 

            \(x\) = 0

    ⇒ y = -3 - 0 

       y = - 3

Vậy giao của d1 và d2 là điểm B(0; -3)