Ba đội đổ nước vào ba bể như nhau. Đội thứ nhất hoàn thành công việc trong 4 giờ, đội thứ hai hoàn thành trong 2 giờ, đội thứ ba hoàn thành trong 5 giờ. Hỏi mỗi đội có số người lần lượt là bao nhiêu? Biết ba đội có tất cả 19 người và năng suất mỗi người là như nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: G là trọng tâm tam giác ABC ⇒IG/AG=1/2⇒2IG/AG=1 Hay GM=AG
Chứng minh tương tự ta có GN=BG và GP=GC
Xét ΔGNM và ΔGBA có:
GN=BG
∠NGM=∠BGA(đối đỉnh)
GM=GA(cmt)
⇒ΔGNM = ΔGBA(c.gc)⇒MN=AB
chứng minh tương tự ta có: PN=BC, PM=AC
Xét ΔMNK và ΔABC có:
MN=AB
PN=CB
PM=CA
⇒ tg MNP=tg ABC(c.c.c)
b) PN cắt AM tại Q. Xét ΔGPQ và ΔGCI có:
GP = GC
D1ˆ=C1ˆ
PGQˆ=CGIˆ
⇒ ΔGPQ = ΔGCI (g.c.g)
⇒ PQ = IC và GQ = GI
Mà PQ = IC, IC = 1/2BC; PN = BC ⇒ PQ = 1/2PN hay PQ = QN
Vậy MQ là trung tuyến thuộc cạnh PN của ΔPNM
Cmtt
=> G là trọng tâm của tam giác NMP.
Chúc em học tốt nha!☘
Ta có: G là trọng tâm tam giác ABC ⇒IG/AG=1/2⇒2IG/AG=1 Hay GM=AG
Chứng minh tương tự ta có GN=BG và GP=GC
Xét ΔGNM và ΔGBA có:
GN=BG
∠NGM=∠BGA(đối đỉnh)
GM=GA(cmt)
⇒ΔGNM = ΔGBA(c.gc)⇒MN=AB
chứng minh tương tự ta có: PN=BC, PM=AC
Xét ΔMNK và ΔABC có:
MN=AB
PN=CB
PM=CA
⇒ tg MNP=tg ABC(c.c.c)
b) PN cắt AM tại Q. Xét ΔGPQ và ΔGCI có:
GP = GC
D1ˆ=C1ˆ
PGQˆ=CGIˆ
⇒ ΔGPQ = ΔGCI (g.c.g)
⇒ PQ = IC và GQ = GI
Mà PQ = IC, IC = 1/2BC; PN = BC ⇒ PQ = 1/2PN hay PQ = QN
Vậy MQ là trung tuyến thuộc cạnh PN của ΔPNM
Cmtt
=> G là trọng tâm của tam giác NMP.

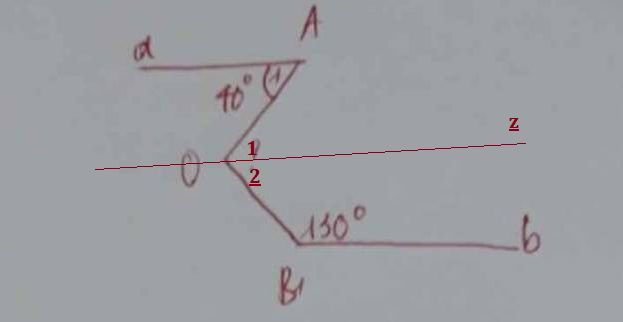
Kẻ đường thẳng `z` đi qua `O` và `// Aa` và `Bb`
`@Aa //// Oz =>\hat{A}=\hat{O_1}` (`2` góc so le trong)
`=>\hat{O_1}=40^o`
`@Bb //// Oz=>\hat{B}+\hat{O_2}=180^o` (Tổg `2` góc trog cùng phía `= 180^o`)
`=>130^o +\hat{O_2}=180^o =>\hat{O_2}=50^o`
Ta có:`\hat{O_1}+\hat{O_2}=\hat{AOB}`
`=>40^o +50^o =\hat{AOB}`
`=>\hat{AOB}=90^o`
Kẻ tia \(Ox\) song song với \(Aa\) (\(Ox\) nằm giữa \(OA,OB\))
suy ra \(Ox\) cũng song song với \(Bb\).
\(\widehat{AOx}=\widehat{A_1}=40^o\) (hai góc so le trong)
\(\widehat{BOx}+\widehat{B_1}=180^o\) (hai góc trong cùng phía)
\(\Leftrightarrow\widehat{BOx}=180^o-\widehat{B_1}=180^o-130^o=50^o\)
\(\widehat{AOB}=\widehat{AOx}+\widehat{BOx}=40^o+50^o=90^o\)

a) \(\Delta ABC=\Delta ADE\left(c.g.c\right)\) suy ra \(BC=DE\).
b) \(\widehat{DAC}=\widehat{BAD}+\widehat{ABC}=90^o+90^o=180^o\) suy ra \(D,A,C\) thẳng hàng.
Tương tự \(B,A,E\) thẳng hàng.
Ta có: \(\widehat{BDA}=\widehat{ACE}=45^o\) mà hai góc này ở vị trí so le trong suy ra \(BD\) song song với \(CE\).
d) \(\widehat{DAM}=\widehat{HAC}\) (hai góc đối đỉnh)
\(\widehat{HAC}=\widehat{ABC}\) (vì cùng phụ với góc \(\widehat{ACB}\))
\(\widehat{ABC}=\widehat{EDA}\) (vì tam giác \(ABC\) bằng tam giác\(ADE\))
suy ra \(\widehat{DAM}=\widehat{EDA}\) suy ra tam giác \(MDA\) cân tại \(M\).
Suy ra \(MA=MD\).
Tương tự ta cũng chứng minh được \(MA=ME\).
Suy ra \(MA=\dfrac{1}{2}\left(ME+MD\right)=\dfrac{DE}{2}\).

`a)`
Có: `x/3=[2x]/6` `y/4=[3y]/12`
Áp dụng t/c của dãy tỉ số bằng nhau có:
`[2x]/6=[3y]/12=z/7=[2x+3y-z]/[6+12-7]=186/11`
`@[2x]/6=186/11=>x=[186.6]/[11.2]=558/11`
`@[3y]/12=186/11=>y=[186.12]/[3.11]=744/11`
`@z/7=186/11=>z=[186.7]/11=1302/11`
____________________________________________________
`b)` Thiếu dữ kiện: `2x-3y+z=..??..`
\(a,\) Ta có: \(\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20}\\\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{20}=\dfrac{z}{28}\end{matrix}\right.\Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\Rightarrow\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{z}{28}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{z}{28}=\dfrac{2x+3y+z}{30+60+28}=\dfrac{186}{62}=3\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{2x}{30}=3\Rightarrow2x=90\Rightarrow x=45\\\dfrac{3y}{60}=3\Rightarrow3y=180\Rightarrow y=60\\\dfrac{z}{28}=3\Rightarrow z=84\end{matrix}\right.\)
\(b,\) Cậu bổ sung đề nhé.


\(3^{n+1}=9^2\)
\(3^{n+1}=\left(3^2\right)^2\)
\(3^{n+1}=3^4\)
=> n+1 =4
=> n =4-1=3

\(\dfrac{2^{15}\cdot9^4}{6^6\cdot8^3}\) \(=\dfrac{2^{15}\cdot\left(3^2\right)^4}{\left(2\cdot3\right)^6\cdot\left(2^3\right)^3}=\dfrac{2^{15}\cdot3^8}{2^6\cdot3^6\cdot2^9}=\dfrac{2^{15}\cdot3^8}{2^{15}\cdot3^6}=3^2=9\)

(-5)2.(-5)=(-5)3=-125
\(\left(\dfrac{1}{2}\right)^2.\left(\dfrac{1}{2}\right)^3.\dfrac{1}{2}\)\(=\left(\dfrac{1}{2}\right)^6=\dfrac{1}{64}\)
\(\left(\dfrac{7}{8}\right)^{11}:\left(\dfrac{7}{8}\right)^{10}=\dfrac{7}{8}\)
\(\left(\dfrac{1}{5}\right)^5.5^5=\dfrac{1^5}{5^5}.5^5=1\)
\(\dfrac{120^3}{40^3}=\dfrac{3^3.40^3}{40^3}=3^3=27\)
\(\dfrac{45^{10}.5^{20}}{75^{15}}=\dfrac{15^{10}.3^{10}.5^{20}}{15^{15}.5^{15}}=\dfrac{3^{10}.5^5}{15^5}=\dfrac{3^5.15^5}{15^5}=3^5=243\)
\(\dfrac{2^{15}.9^4}{6^6.8^3}=\dfrac{2^{15}.\left(3^2\right)^4}{2^6.3^6.\left(2^3\right)^3}=\dfrac{2^{15}.3^8}{2^6.3^6.2^9}=3^2=9\)
mấy cái này dễ quá toàn nhân chia lũy thừa cùng cơ số bạn tự làm nhé. mình làm hộ 3 câu dưới thôi.
\(\dfrac{120^3}{40^3}\) = ( \(\dfrac{120}{40}\)) 3 = 33 = 27
\(\dfrac{45^{10^{ }}.5^{20}}{75^{15}}\) = \(\dfrac{3^{20^{ }}5^{30}}{3^{15}5^{30}}\) = 35 = 243
\(\dfrac{2^{15^{ }}.9^4}{6^6.8^3}\) = \(\dfrac{2^{15^{ }}.3^8}{2^{6^{ }}.3^{6^{ }}.2^9}\) = 32 = 9
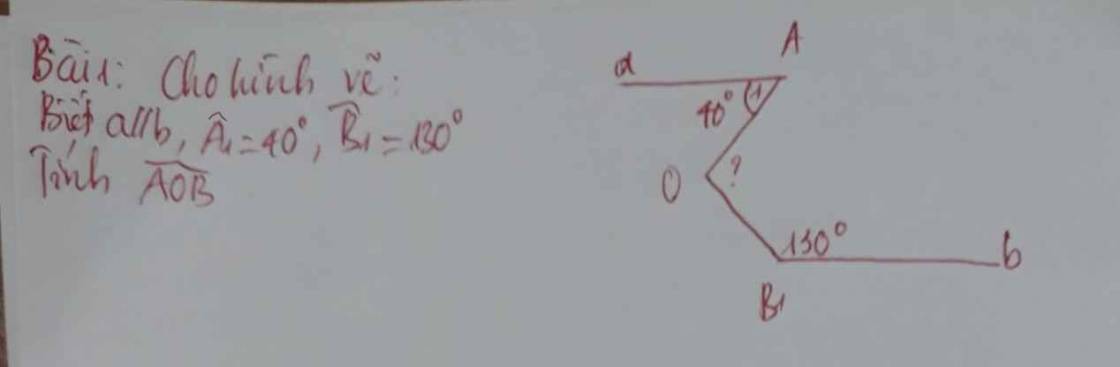
Gọi số người của ba đội lần lượt là: x; y; z (x; y; z > 0)
Ta có: 4x = 2y = 5z
Áp dụng tính chất dãy tỉ số bằng nhau:
$\dfrac{x}{5}$ = $\dfrac{y}{10}$ = $\dfrac{z}{4}$ = $\dfrac{19}{10+4+5}$ = $\dfrac{19}{19}$ = 1
=> $\dfrac{x}{5}$ = 1 \(\times\) 5 = 5 (người)
=> $\dfrac{y}{10}$ = 1 \(\times\) 10 = 10 (người)
=> $\dfrac{z}{4}$ = 1 \(\times\) 4 = 4 (người)
Vậy cả ba đội có số người lần lượt là 5 người; 10 người; 4 người.
Gọi số người của đội `1,2,3` lần lượt là : `a,b,c ( ≠ 0)`
Ta có : `4a = 2b = 5c`
Áp dụng dãy tỉ số bằng nhau :
` a/5 = b/10 = c/4 = (10+4+5)/19 = 1`
`=> a/5 = 1 xx 5 = 5 (người)`
`=> b/10 = 1 xx 10 = 10 (người)`
`=> c/4 = 1 xx 4 = 4 (người)`
Vậy....