\(\dfrac{2033}{2001}\) = 1 + \(\dfrac{32}{2001}\) > 1 + \(\dfrac{32}{2003}\)= \(\dfrac{2035}{2003}\)

vậy \(\dfrac{2033}{2001}\) > \(\dfrac{2035}{2003}\) 

phương pháp so sánh bằng phần hơn : 

áp dụng khi tử 1 - mẫu 1 = tử 2 - mẫu 2;  nếu phân số nào có phần hơn lớn hơn thì phân số đó lớn hơn

32/2001 > 32/ 2003 đúng phải không?

1+ 32/2001 > 1 + 32/2003 thêm 1 vào 2 bên

2033/2001 > 2035/ 2003 quy đồng mẫu số từ phía.

vậy 2033/2001 > 2035/ 2003

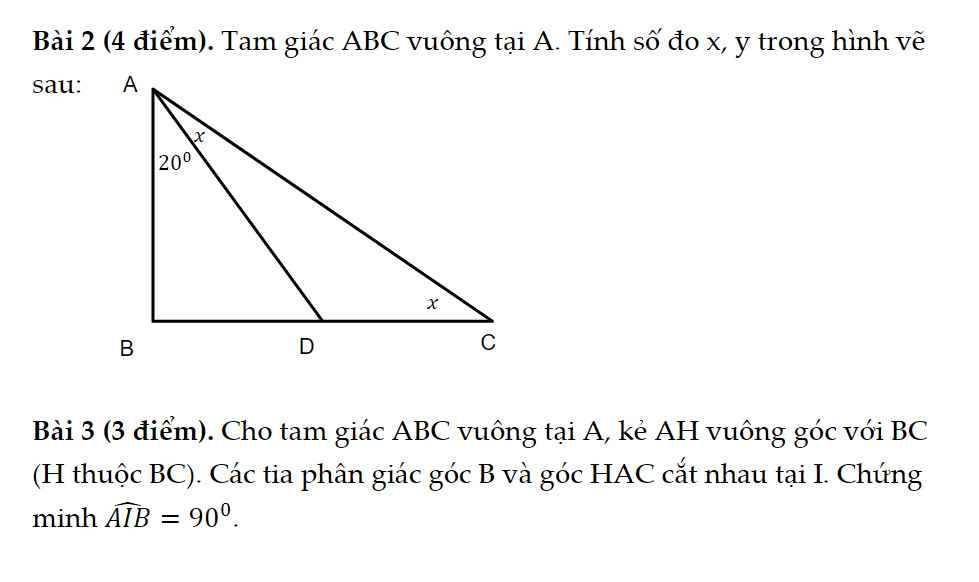
bài 2:
y là cái nào?, nếu x ở A thì y là cái kia " x" đi!
y = 90 - 20 - x = 70 - x
sin y = sin ( 70 - x) = AB: AC.
Nếu BD = DC thì kết quả là y = 45 ^o và x = 25 ^o 

? vì không có giờ nên để lại đây. làm tiếp nhé!

888 + 88 + 8 + 8 + 8 = 1000

Bạn tự vẽ hình nhé <3

a, Xét △EIB và ΔEDB có:

EB chung

Góc EDB = Góc EIB (=90 độ)

Góc DEB = Góc IEB (pg EB)

⇒△EIB = ΔEDB (ch-gn)

b, Xét △DHB và △IFB có:

góc HDB = góc FIB (=90 độ)

góc HBD = góc FBI (đối đỉnh)

BD = IB (△EIB = ΔEDB)

⇒ △DHB = △IFB (g.c.g)

c, Ta có HB = BF ( △DHB = △IFB)

mà DB < HB (cgv < c.huyền)

⇒ DB < BF 

d, Ta có ED = EI (△EIB = ΔEDB)

             DH = IF (△DHB = △IFB)

⇒ ED + DH = EI + IF

⇒     EH      =     EF

Xét △EHK và △EFK có:

EH = EF (cmt)

EK chung

HK = KF (K là trung điểm HF)

⇒△EHK = △EFK (c.c.c)

⇒ Góc HEK = Góc FEK ( góc t.ứng)

⇒ EK là phân giác góc HEF

 mà EB là phân giác góc HEF

⇒ E, B, K thẳng hàng

`1/2xx1/2xx1/2xx1/2xx1/2`

`=(1xx1xx1xx1xx1xx1)/(2xx2xx2xx2xx2xx2)`

`=1/64`

\(\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{32}\)

giờ bạn cần nữa ko mình giải cho

a) ta có: AB2 + AC2 = 100; BC2 = 100 => AB2 + AC2 = BC2

a) ta có: AB2 + AC2 = 100; BC2 = 100 => AB2 + AC2 = BC2

=> △ABC vuông tại A (theo định lý Py-ta-go)

b) ta có MK là tia đối của MH; MK = MH mà MH lại vuông góc với tia AC => MK vuông góc với tia BK

Ta có KH vuông góc với AH; BA vuông góc với HA; HK vuông góc với BK => ABKH là 1 hình chữ nhật => BK // AH => BK // AC (vì H ϵ AC)

c) xét △BKM và △AHM có:

     góc BKM = Góc AHM = 90o (vì ABKH là HCN)

     KB = HA (vì ABKH là HCN)

     MK = MH (theo GT)

=> △BKM = △AHM (2 cạnh góc vuông)

=> BM = AM (2 cạnh tương ứng)

có AM = BM mà BM = CM => AM = CM

xét △AMH và △CMH có

     góc AHM = góc CHM = 90o (theo GT)

     AM = CM (theo c/m trên)

     MH: cạnh chung

=> △AMH = △CMH (cạnh huyền - cạnh góc vuông)

=> AH = CH => H là trung điểm của AC

Vì M là trung điểm của BC nên AM là 1 đường trung tuyến; Vì H là trung điểm của AC nên BH là 1 đường trung tuyến => giao của BH và AM hay điểm G là trọng tâm của △ABC

Vì M là trung điểm của BC nên AM là 1 đường trung tuyến; Vì H là trung điểm của AC nên BH là 1 đường trung tuyến => giao của BH và AM hay điểm G là trọng tâm của △ABC

a/

\(BC^2=10^2=100\)

\(AB^2+AC^2=6^2+8^2=100\)

\(\Rightarrow BC^2=AB^2+AC^2\Rightarrow\Delta ABC\) vuông tại A (Pitago đảo)

b/

Xét tg MHC và tg MKB có

MH=MK (gt)

MB=MC (gt)

\(\widehat{HMC}=\widehat{KMB}\) (góc đối đỉnh)

\(\Rightarrow\Delta MHC=\Delta MKB\) (c.g.c)\(\Rightarrow\widehat{CHM}=\widehat{BKM}=90^o\)

\(\Rightarrow BK\perp HK\) mà \(MH\perp AC\Rightarrow AC\perp HK\)

=> BK//AC (cùng vuông góc với HK)

c/

Xét tg vuông ABC có MB=MC (gt) => AM là trung tuyến thuộc cạnh huyền \(\Rightarrow AM=\dfrac{BC}{2}=MB=MC\) (trong tg vuông trung tuyến thuộc cạnh huyền thì bằng nửa cạnh huyền)

=> tg MAC cân tại M

Mà \(MH\perp AC\) => MH là đường cao của tg MAC => MH là trung tuyến của tg MAC (trong tg cân đường cao xuất phát từ đỉnh tg cân đồng thời là đường trung tuyến)

=> HA=HC => BH là trung tuyến của tg ABC 

mà AM là trung tuyến của tg ABC 

=> G là trọng tâm của tg ABC

a) ta có: AB² + AC² = 100; BC² = 100 => AB² + AC² = BC²

=> △ABC vuông tại A (theo định lý Py-ta-go)

b) ta có MK là tia đối của MH; MK = MH mà MH lại vuông góc với tia AC => MK vuông góc với tia BK

Ta có KH vuông góc với AH; BA vuông góc với HA; HK vuông góc với BK => ABKH là 1 hình chữ nhật => BK // AH => BK // AC (vì H ϵ AC)

c) xét △BKM và △AHM có:

     góc BKM = Góc AHM = 90^o (vì ABKH là HCN)

     KB = HA (vì ABKH là HCN)

     MK = MH (theo GT)

=> △BKM = △AHM (2 cạnh góc vuông)

=> BM = AM (2 cạnh tương ứng)

có AM = BM mà BM = CM => AM = CM

xét △AMH và △CMH có

     góc AHM = góc CHM = 90^o (theo GT)

     AM = CM (theo c/m trên)

     MH: cạnh chung

=> △AMH = △CMH (cạnh huyền - cạnh góc vuông)

=> AH = CH => H là trung điểm của AC

Vì M là trung điểm của BC nên AM là 1 đường trung tuyến; Vì H là trung điểm của AC nên BH là 1 đường trung tuyến => giao của BH và AM hay điểm G là trọng tâm của △ABC