
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(x\inƯ\left(32\right)\) và \(x>5\)
\(Ư\left(32\right)=\left\{1;2;4;8;16;32\right\}\)
\(\Rightarrow x\in\left\{8;16;32\right\}\)

2111 + 5687 = 7798
9807 + 8079 = 17886
9000 + 8000 = 17000
8904 + 7909 = 16813
7111 + 9000 = 16111
2111 + 5687 = 7798
9807 + 8079 = 17886
9000 + 8000 = 17000
8904 + 7909 = 16813
7111 + 9000 = 16111

Bài 1:
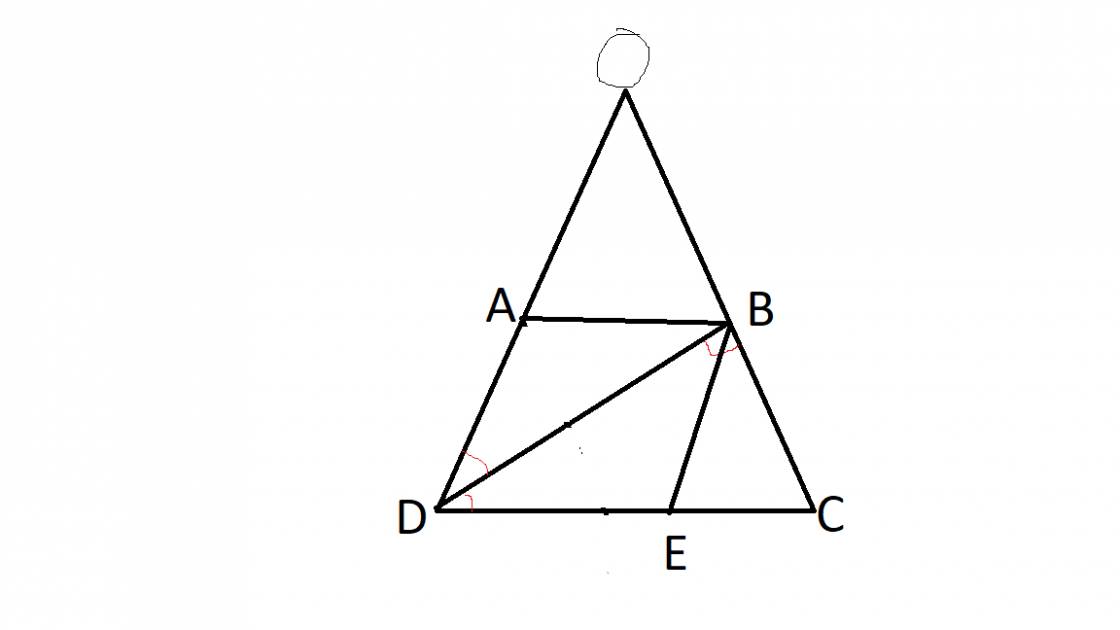
Ta có: AD=BC=3cm (t/c hthang)
Vì AB//CD(gt) nên \(\widehat{ABD}=\widehat{BDC}\left(SLT\right)\)
Mà \(\widehat{ADC}=\widehat{BDC}\) (do BD là tia pgiac góc D)
=>∠ABD=∠BDC
=>∆ABD cân tại A
=>AD=BC=3cm
Vì ∆DBC vuông tại B
nên ∠BDC+∠C=90o
Mà ∠ADC=∠C (do ABCD là hình thang cân)
và ∠BDC=1/2 ∠ADC
=> ∠BCD=1/2∠C
Khi đó: ∠C+1/2∠C=90o=>∠C=60o
- Kẻ từ B 1 đường thẳng // AD cắt CD tại E
Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE
⇒ DE = 3 (cm), BE = 3 (cm)
Mà ∠BEC=∠ADC(đồng vị)
=>∠BEC=∠C
=>∆BEC cân tại B có ∠C=60o
=>∆BEC là ∆ cả cân cả đều
=> EC=BC=3cm
Ta có: CD = CE + ED = 3 + 3 = 6(cm)
Chu vi hình thang ABCD bằng:
AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)
Bài 2:
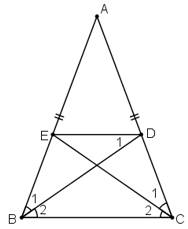
Ta có: ∆ABC là ∆ cân tại A(gt)
=>∠ABC=∠ACB
+Ta có BD là tia pgiac của ∠ABC
=>∠B1=∠B2=1/2∠ABC
+Ta có CE là tia pgiac ∠ACB
=>C1=C2=1/2∠ACB
Xét ∆
AEC và ΔADB có:
+∠A chung
+AB=AC
+C1=B1
=> ΔAEC = ΔADB
=> AE = AD
=>BCDE là hình thang cân
b) Ta có ∠ACB=∠ABC=50o(do BCDE là hình thang cân)
Ta có: ED//BC
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABC}=\widehat{AED}\\\widehat{ACB}=\widehat{ADE}\end{matrix}\right.=50^o}\) (SLT)
Mà ∠DEB=∠EDC
Ta có:
+∠DEB+∠AED=180o (kề bù)
=>50o+∠AED=180o
=>∠AED=180o-50o=130o
=>∠AED=∠ADE=130o

(1,1 + 2,21+...+9,1)(3,5.6,3 - 4,5.4,9)
= (1,1 + 2,21 +...+9,1).( 22,05 - 22,05)
= (1,1+ 2,21+...+9,1).0
= 0

Gọi số cần tìm là: \(\overline{abc}\left(a\ne0;\right)a,b,c\inℕ\)
Ta có \(\overline{abc}=a.100+b.10+c=98a+7b+2a+3c=98\left(a+b+c\right)+\left(a+2b\right)\)
Theo đề bài vì abc chia hết cho 7;98a;7b;a+b+c
Mà a+2b có kết quả lớn nhất bằng 9+2.9=2 => a+2b có thể = 7, 14, 21
-Nếu a+2b=7 mà 2b là số chẵn =>a<7 và a là số lẻ => a= 1;3;5 <=>b=3;2;1
Ta ghép vào ta có:
+ Với a=1; b=3=> a+b=4 mà tổng a+b+c⁝7
=>c=3=> \(\overline{abc}=133\)
+ Với a=3; b=2 =>a+b=5=>c=2 hoặc 9
=> \(\overline{abc}=322;329\)
Tương tự: Nếu a+2b=14=>a=2;4;6 và b=6;5;4;3
+Với a=2; b=6=>... (như ý trên) => số đó =455
+Với a=6;b=4=>... =>644
+Với a=8;b=3=>...=>833
-Nếu a+2b=21=>a= 3;5;7;9 và b=9;8;7;6
+Với a=3;b=9=>c=2;9=>392 và 399
+Với a=5;b=8=>c=1,8=>581 và 588
+Với a=7;b=7=>c=0,7=>770 và 777
+ Với a=9; b=6=>c=6=> 966
Vậy số tự nhiên đó là: 133;322;329;266;455;644;833;392;399;581;588;770;777;966

Bài 3:
P = \(\dfrac{1^2}{2^2-1}\). \(\dfrac{3^2}{4^2-1}\).\(\dfrac{5^2}{6^2-1}\).....\(\dfrac{2023^2}{2024^2-1}\)
P = \(\dfrac{1}{\left(2-1\right).\left(2+1\right)}\).\(\dfrac{3^2}{\left(4-1\right).\left(4+1\right)}\)....\(\dfrac{2023^2}{\left(2024-1\right).\left(2024+1\right)}\)
P = \(\dfrac{1}{1.3}\).\(\dfrac{3^2}{3.5}\).\(\dfrac{5^2}{5.7}\).\(\dfrac{7^2}{7.9}\)......\(\dfrac{2021^2}{2021.2023}\).\(\dfrac{2023^2}{2023.2025}\)
P = \(\dfrac{1}{2025}\)

Đây là dạng tìm một số khi biết giá trị phần trăm của nó.
Kiến thức cần nhớ: muốn tìm một số khi biết giá trị phần trăm của số đó, ta lấy giá trị đó chia cho số phần trăm rồi nhân với 100
25% của một số là 25
Số đó là: 25: 25 \(\times\) 100 = 100
Đáp số: 100

\(58,7\times9,1-12,4\times58,7+3,3\times58,7\)
\(=58,7\times\left(9,1-12,4+3,3\right)\)
\(=58,7\times0\)
\(=0\)
Chúc bạn học tốt
58,7 × 9,1 - 12,4 × 58,7 + 3,3 × 58,7
=58,7x(9,1-12,4+3,3)
=58,7x0
=0
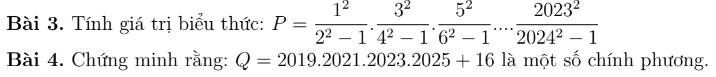
Có bao nhiêu số tự nhiên \(x\) \(\in\) B(11) và 20 < \(x\) ≤ 150
Các số tự nhiên lớn hơn 20 mà nhỏ hơn 150 đồng thời chia hết cho 11 là các số thuộc dãy số sau:
22; 33; 44; 55;...;143
Dãy số trên là dãy số cách đều với khoảng cách là: 33- 22 = 11
Dãy số trên có số số hạng là: (143 - 22): 11 = 12 (số)
Kết luận: Vậy có 12 số tự nhiên \(x\) \(\in\) B(11) và 20 < \(x\) ≤ 150