\(\dfrac{11}{4}\times49:\dfrac{77}{2}\)

\(=\dfrac{11}{4}\times\dfrac{49}{1}\times\dfrac{2}{77}\)

\(=\dfrac{11}{4}\times\dfrac{2}{77}\times49\)

\(=\dfrac{1}{2}\times\dfrac{1}{7}\times49\)

\(=\dfrac{1}{14}\times49\)

\(=\dfrac{49}{14}=\dfrac{7}{2}=3,5\)

đề bài là j vậy bạn

6,4 m ứng với số phần trăm là:

  86% - 78% = 8% (số mét vải xanh)

Số mét vải xanh cửa hàng có là:

  6,4 : 8 x 100 = 80 (m)

Đáp số...

\(6,4m\) vải ứng với:

\(86\%-78\%=8\%\left(số.vải.xanh\right)\)

Số \(m\) vải xanh của cửa hàng:

\(6,4:8.100=80\left(m\right)\)

Nếu đang định hướng bằng là bàn thì không nên để hai la bàn gần nhau vì kim la bàn là kim nam châm là vật có tính chất từ nên nếu để hai la bàn gần nhau thì hai kim nam châm sẽ tương tác với nhau khiến kim la bàn bị lệch khỏi hai hướng bắc và nam 

Nếu đang định hướng bằng là bàn thì không nên để hai la bàn gần nhau vì kim la bàn là kim nam châm là vật có tính chất từ nên nếu để hai la bàn gần nhau thì hai kim nam châm sẽ tương tác với nhau khiến kim la bàn bị lệch khỏi hai hướng bắc và nam 

a) Ta có: \(\dfrac{-22}{10}=-\dfrac{22:2}{10:2}=-\dfrac{11}{5}\)

\(\dfrac{11}{-5}=-\dfrac{11}{5}\)

\(\Rightarrow\dfrac{-22}{10}=\dfrac{11}{-5}\)

b) Ta có: \(\dfrac{20}{-52}=-\dfrac{20:4}{52:4}=-\dfrac{5}{13}\)

Mà: \(-\dfrac{5}{13}\ne\dfrac{5}{-14}\)

\(\Rightarrow\dfrac{20}{-52}\ne\dfrac{5}{-14}\)

Ta có: St4 = 14 = 3 + 4 + 7 = st1 + st2 + st3

         ST5 = 25 = 4 + 7 + 14 = st2 + st3 + st4 

Quy luật của dãy số là kể từ số hạng thứ tư trở đi của dãy số, mỗi số hạng trong dãy số bằng tổng của ba số hạng liền kề trước nó.

St6 = st3+ st4 + st5  = 7 + 14 + 25 = 46

ST7 = st4 + st5 + st6 = 14 + 25 + 46 = 85

St8 = st5 + st6 + st7 = 25 + 46 + 85 = 156

Vậy ba số tiếp theo cần điền vào chỗ... của dãy số có quy luật đã cho lần lượt là:

46; 85; 156

3+4

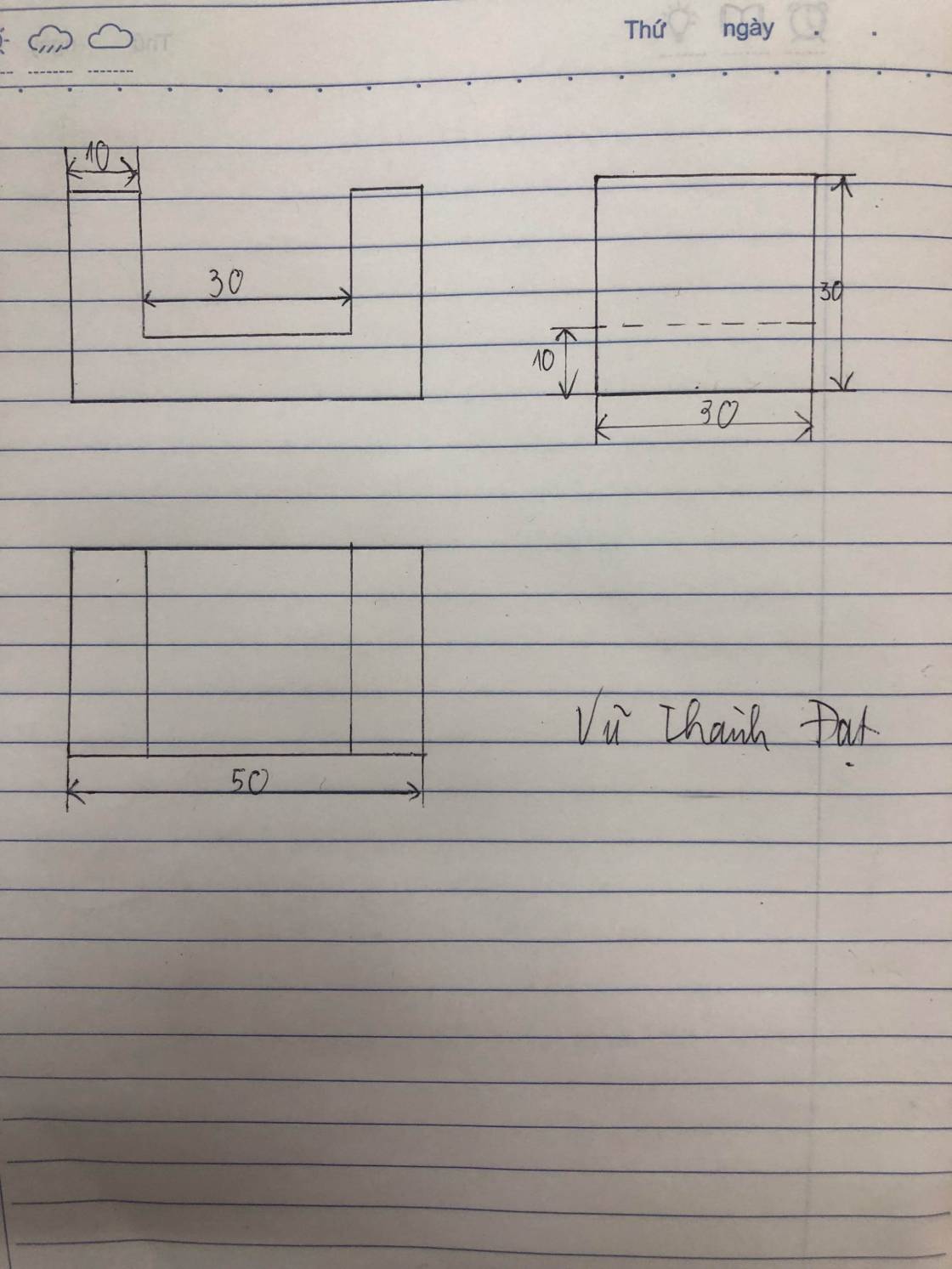
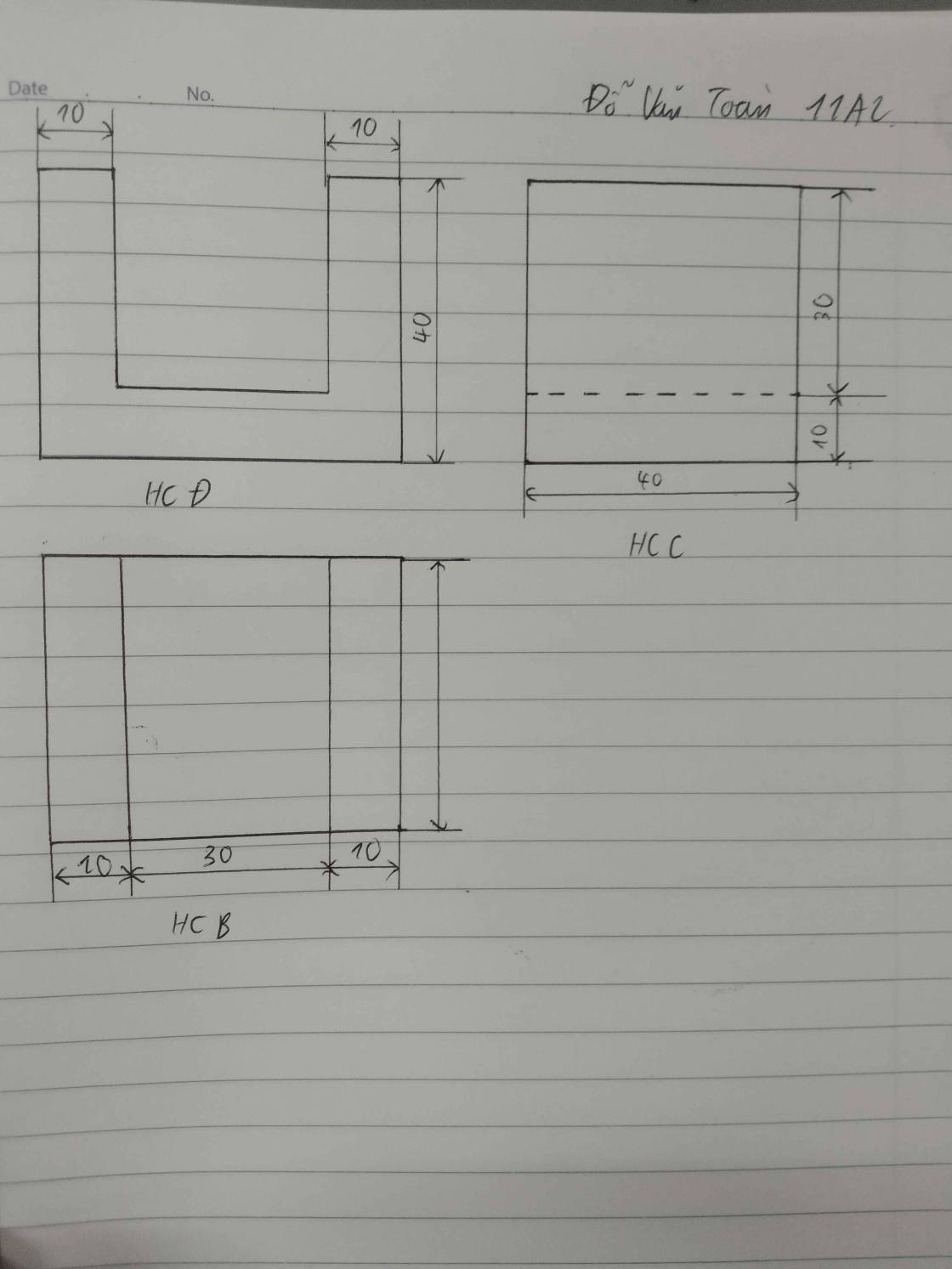
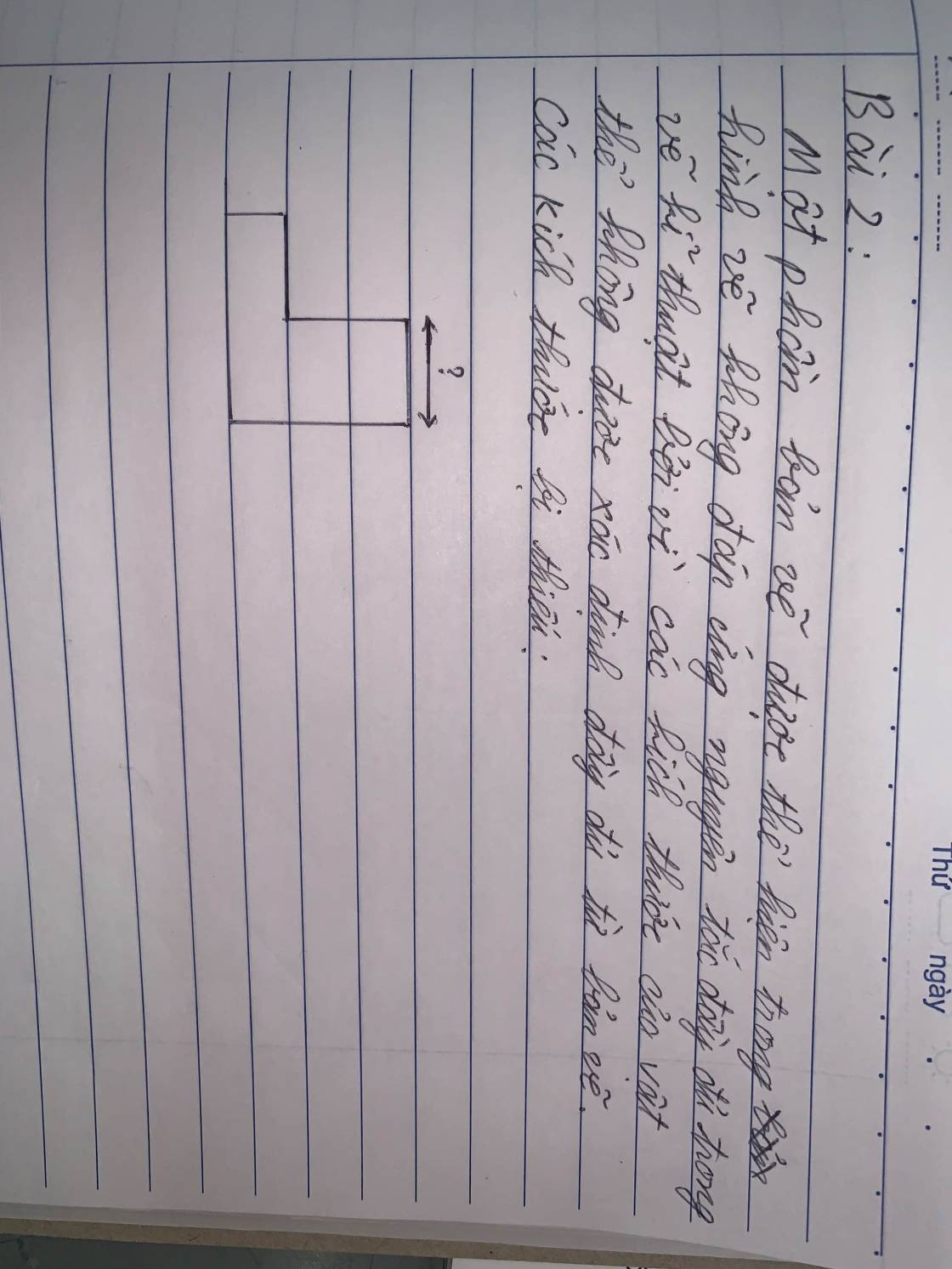
Bản vẽ được thể hiện trong hình vẽ không đáp ứng được nguyên tắc đầy đủ về kĩ thuật là vì bản vẽ thiếu một kích thước nên không thể xác định cụ thể hình ảnh của vật và bản vẽ không có hình khối (3D) mô phỏng hình ảnh của vật 

Kích thước bị thiếu là:

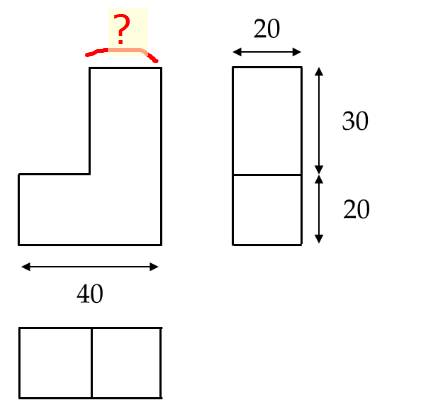
C=(1-5-9+13)+(17-21-25+29)+...+(2013-2017-2021+2025)-2029

C=0+0+0+...+0-2029

C=-2029

C = 1 - 5 - 9 + 13 + 17 - 21 - 25 + 29 + ... + 2013 - 2017 - 2021 + 2025 - 2029

= (1 - 5 - 9 + 13) + (17 - 21 - 25 + 29) + ... + (2001 - 2005 - 2009 + 2013) - 2017 - 2021 + 2025 - 2029

= 0 + 0 + ... + 0 - 4042

= -4042

Bài 1:

Vì p là số nguyên tố lớn hơn 3 nên p là số lẻ

vậy p + 1 và p -  1 là hai số chẵn.

Mà p + 1 - (p - 1) = 2 nên p + 1 và p - 1 là hai số chẵn liên tiếp.

đặt p - 1 = 2k thì p + 1 = 2k + 2 (k \(\in\) N*)

A = (p + 1).(p - 1) = (2k + 2).2k = 2.(k + 1).2k = 4.k.(k +1) 

Vì k và k + 1 là hai số tự nhiên liên tiếp nên chắc chẵn phải có một số chia hết cho 2.

⇒ 4.k.(k + 1) ⋮ 8 

⇒ A = (p + 1).(p - 1) ⋮ 8 ⁽¹⁾

Vì p là số nguyên tố lớn hơn 3 nên p có dạng:

   p = 3k + 1; hoặc p = 3k + 2

Xét trường hợp p = 3k + 1 ta có:

  p - 1 = 3k + 1  - 1  = 3k ⋮ 3

⇒ A = (p + 1).(p - 1) ⋮ 3  ⁽²⁾

Từ (1) và (2) ta có:

A ⋮ 3; 8  ⇒ A \(\in\) BC(3; 8)

3 = 3; 8 = 2³; ⇒ BCNN(3; 8) = 2³.3 = 24

⇒ A \(\in\) B(24) ⇒ A ⋮ 24 (*)

Xét trường hợp p = 3k + 2 ta có

p + 1 = 3k + 2 + 1  = 3k + 3 = 3.(k + 1) ⋮ 3 ⁽³⁾

Từ (1) và (3) ta có: 

A = (p + 1).(p - 1) ⋮ 3; 8 ⇒ A \(\in\) BC(3; 8)

3 = 3; 8 = 2³ ⇒ BCNN(3; 8) = 2³.3 = 24 

⇒ A \(\in\) BC(24) ⇒ A \(⋮\) 24 (**)

Kết hợp (*) và(**) ta có

A \(⋮\) 24 (đpcm)

Cảm ơn cô

Lời giải:

Gọi $d=ƯCLN(x+2022, x+2015)$

$\Rightarrow (x+2022)-(x+2015)\vdots d$

$\Rightarrow 7\vdots d$

$\Rightarrow d=1$ hoặc $d=7$

Nếu $d=1$ thì $x+2022, x+2015$ nguyên tố cùng nhau

$\Rightarrow (x+2022)^2, (x+2015)^3$ nguyên tố cùng nhau 

$\Rightarrow$ để $(x+2022)^2=64(x+2015)^3$ thì:

$x+2015=1, (x+2022)^2=64$

$\Rightarrow x=-2014$ (tm)

Nếu $d=7$ thì đặt $x+2022=7a, x+2015=7b$ với $a,b$ nguyên tố cùng nhau.

Khi đó: $(7a)^2=64(7b)^3$

$\Rightarrow a^2=448b^3$
Vì $(a,b)=1$ nên $b=1; a^2=448$ (vô lý vì 448 không là scp)

Vậy.......