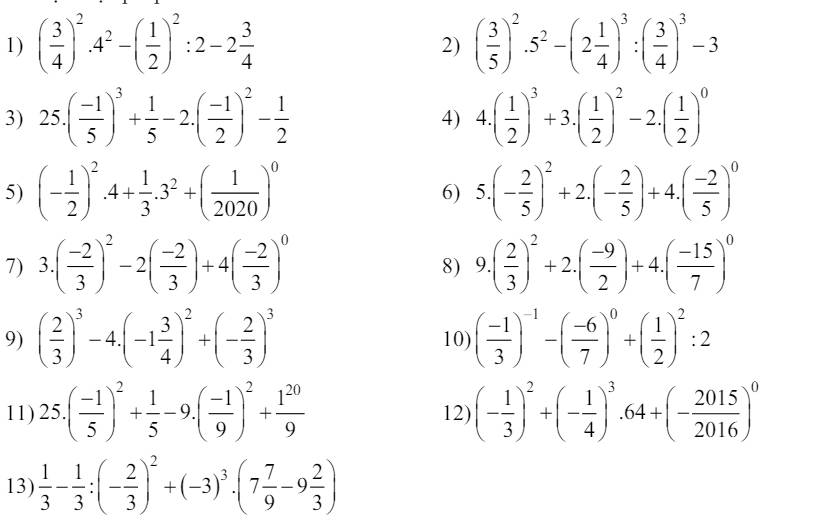
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) vì M nằm giữa đoạn thẳng AB nên ta có :
AM + MB = AB
AM + MB = 12 cm
Mà MA = MB = 12 : 2 = 6 cm
Vậy MB dài 6cm
b) Câu b bị thiếu đề nên mik ko giải dc =(

Lời giải:
\(1-A=\frac{10^{2023}-10^{2022}}{10^{2023}+2024}=\frac{9.10^{2022}}{10^{2023}+2024}=\frac{9}{10+\frac{2024}{10^{2022}}}< \frac{9}{10}=1-\frac{1}{10}=1-\frac{10^{2023}}{10^{2024}}=1-B\)
$\Rightarrow A>B$

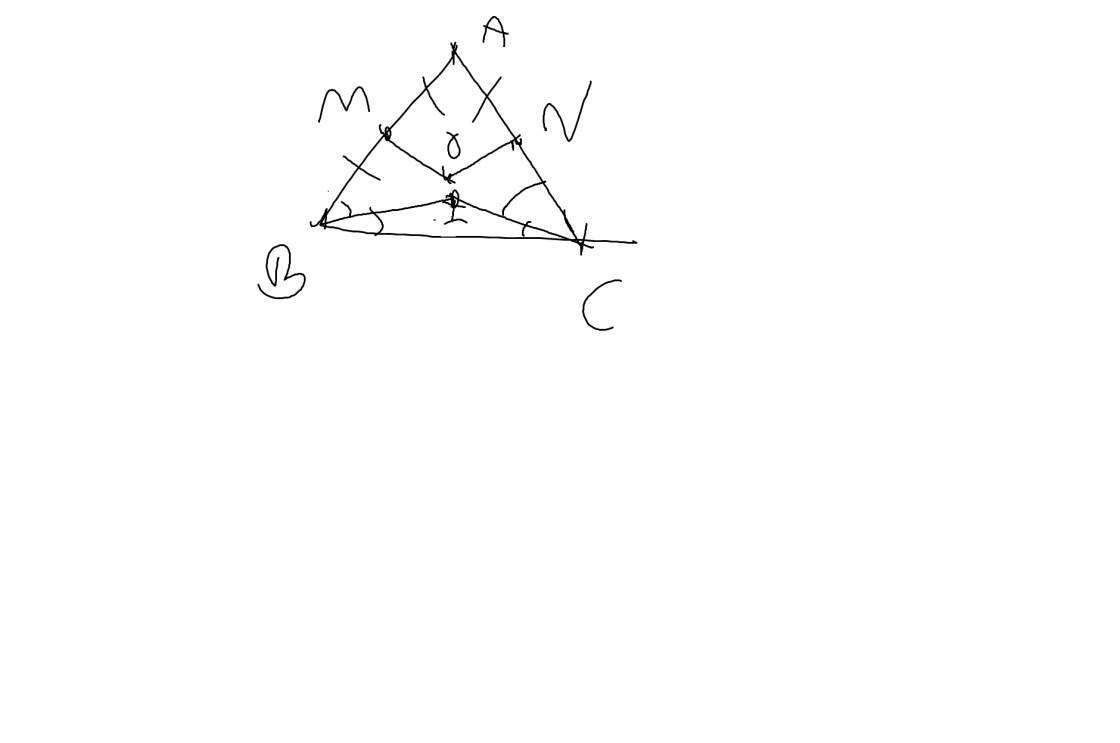
a: ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC
nên AM=MB=AN=NC
Xét ΔAMO vuông tại M và ΔANO vuông tại N có
AO chung
AM=AN
Do đó: ΔAMO=ΔANO
b: O nằm trên đường trung trực của AB
=>OA=OB
O nằm trên đường trung trực của AC
=>OA=OC
Do đó: OA=OB=OC
c: Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
=>\(\widehat{BAO}=\widehat{CAO}\)
=>AO là phân giác của góc BAC
d: Ta có: \(\widehat{IBC}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ICB}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
=>I nằm trên đường trung trực của BC(1)
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,O,I thẳng hàng

\(125\times x-25\times x=5208\)
\(x\times\left(125-25\right)=5208\)
\(x\times100=5208\)
\(x=5208:100\)
\(x=52,08\)
X*125- X*25= 5208
X*(125-25) = 5208
X*100 = 5208
X= 5208:100
X= 52,08.
Đây nek, đúng 100% luôn nên k cho mik nha!

Lời giải:
Vì số tự nhiên đó chia 17 dư 7 nên đặt nó là $A=17k+7$ với $k$ là số tự nhiên.
$A=17k+7$ chia 7 dư 4
$\Rightarrow 17k+7-4\vdots 7$
$\Rightarrow 17k+3\vdots 7$
$\Rightarrow 17k+3+14\vdots 7$
$\Rightarrow 17(k+1)\vdots 7\Rightarrow k+1\vdots 7$
$\Rightarrow k=7m-1$ với $m$ tự nhiên.
Khi đó: $A=17k+7=17(7m-1)+7=119m-10=119(m-1)+109$
Vậy số đó chia 119 dư 109.

Thời gian ô tô đi từ A đến B là:
8h50p-6h30p=2h20p=7/3(giờ)
Độ dài quãng đường AB là \(50\times\dfrac{7}{3}=\dfrac{350}{3}\left(km\right)\)
quãng đường đi từ ab là:
8 giờ 50 phút - 6 giờ 30 phút=2 giờ 20 phút
đáp số:2 giờ 20 phút

\(\dfrac{34}{15}\times\dfrac{3}{17}=\dfrac{34}{17}\times\dfrac{3}{15}=2\times\dfrac{1}{5}=\dfrac{2}{5}\)
1; (\(\dfrac{3}{4}\))2. 42 - (\(\dfrac{1}{2}\))2 : 2 - 2\(\dfrac{3}{4}\)
= \(\dfrac{3^2}{4^2}\).42 - \(\dfrac{1}{4}\) : 2 - 2\(\dfrac{3}{4}\)
= 9 - \(\dfrac{1}{8}\) - \(\dfrac{11}{4}\)
= \(\dfrac{72}{8}\) - \(\dfrac{1}{8}-\dfrac{22}{8}\)
= \(\dfrac{71}{8}\) - \(\dfrac{22}{8}\)
= \(\dfrac{49}{8}\)
2; (\(\dfrac{3}{5}\))2.52 - (2\(\dfrac{1}{4}\))3 : (\(\dfrac{3}{4}\))3 - 3
= \(\dfrac{9}{5^2}\).52 - (\(\dfrac{9}{4}\))3 : (\(\dfrac{3}{4}\))3 - 3
= 9 - (\(\dfrac{9}{4}\) : \(\dfrac{3}{4}\))3 - 3
= 9 - 33 - 3
= 9 - 27 - 3
= 9 - (27 + 3)
= 9 - 30
= - 21