Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C D E M N
1/ Xét tg ABC và tg DBE có
BA=BD (gt)
DE//AC (gt) \(\Rightarrow\widehat{BAC}=\widehat{BDE}\) (góc so le trong)
\(\widehat{ABC}=\widehat{DBE}\) (góc đối đỉnh)
=> tg ABC = tg DBE (g.c.g)
2/
Ta có tg ABC = tg DBE (cmt) => BC=BE
Xét tư giác ACDE có
BA=BD (gt); BC=BE (cmt) => ACDE là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AE//CD (cạnh đối hbh)
3/
Xét tg ADC có
MA=MC (gt); BA=BD (gt) => BM là đường trung bình của tg ADC
=> BM//CD
Xét tg ADE có
BA=BD (gt); NE=ND (gt) => BN là đường trung bình của tg ADE
=> BN//AE
Mà CD//AE (cạnh đối hbh)
=> BM//AE (cùng //CD)
\(\Rightarrow BN\equiv BM\) (từ 1 điểm ngoài đường thẳng cho trước chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)
=> M, B, N thẳng hàng

Ta có: \(\left\{{}\begin{matrix}\left|2y-27\right|^{2023}\ge0\forall y\\\left(3x+10\right)^{2024}\ge0\forall x\end{matrix}\right.\)
\(\Rightarrow\left|2y-27\right|^{2023}+\left(3x+10\right)^{2024}\ge0\forall x,y\)
Mà: \(\left|2y-27\right|^{2023}+\left(3x+10\right)^{2024}=0\)
nên: \(\left\{{}\begin{matrix}2y-27=0\\3x+10=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=\dfrac{27}{2}\\x=-\dfrac{10}{3}\end{matrix}\right.\)
Vậy: ...

Vì DE // BC nên:
\(ADE=DBC=80^o\) ( 2 góc đồng vị )
Vì ADE và EDB là 2 góc kề bù nên ta có:
\(EDB+ADE=180^o\)
Hay \(EDB+80^o=180^o\)
\(EDB=180^o-80^o\)
\(EDB=100^o\)
Vậy \(ADE=80^o;EDB=100^o\)

Olm chào em, olm cảm ơn em đã lựa chọn đồng hành cùng olm, cảm ơn những đánh giá của em về chất lượng bài giảng của olm.
Olm chúc học tập vui vẻ và hiệu quả cùng olm em nhé.

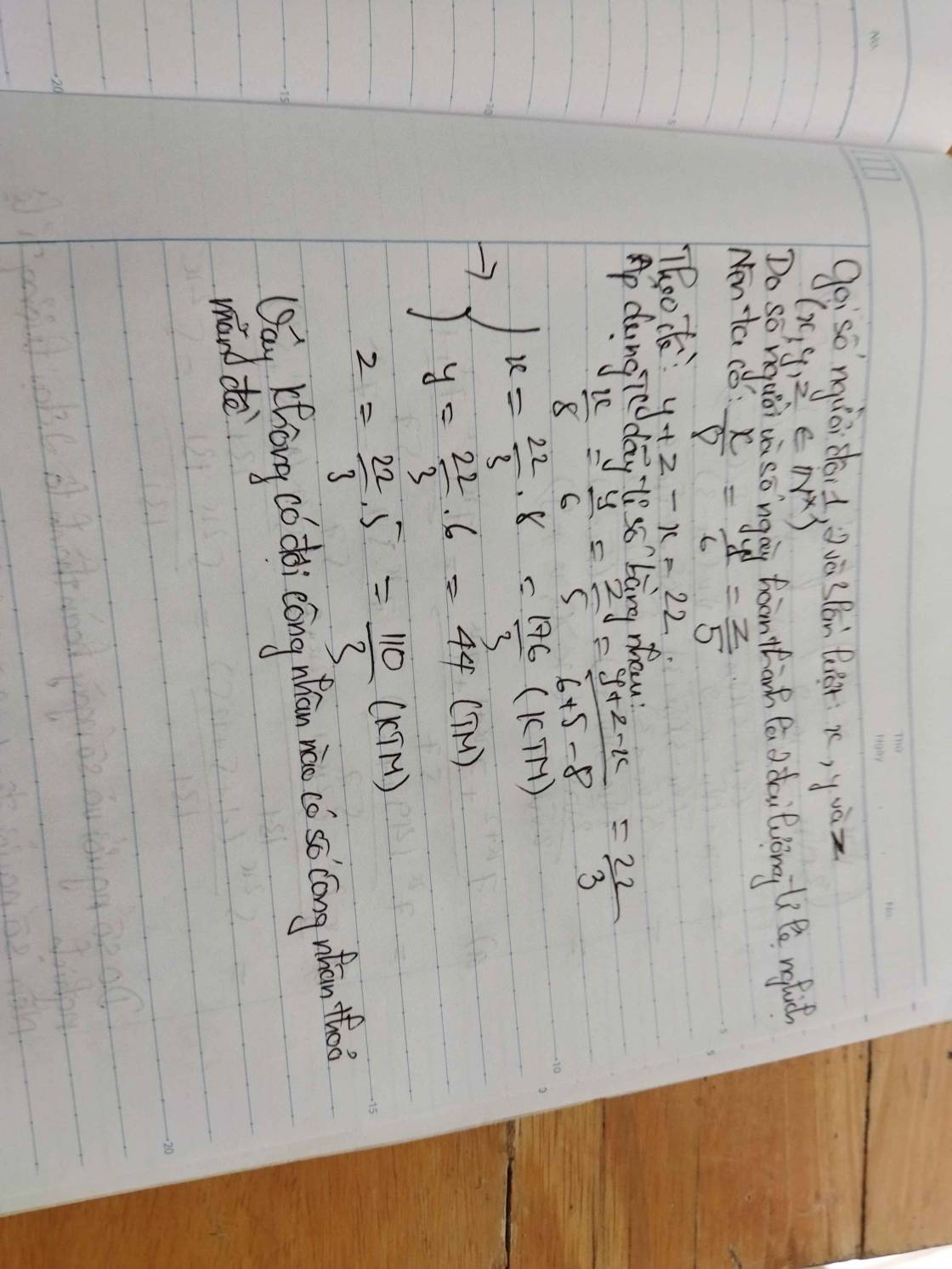


Lời giải:
$\frac{5}{3}(-\frac{6}{5}+x)-\frac{1}{4}(\frac{2}{3}-1)=\frac{-3}{8}$
$-2+\frac{5}{3}x+\frac{1}{12}=\frac{-3}{8}$
$\frac{5}{3}x-\frac{23}{12}=\frac{-3}{8}$
$\frac{5}{3}x=\frac{23}{12}+\frac{-3}{8}=\frac{37}{24}$
$x=\frac{37}{24}: \frac{5}{3}=\frac{37}{40}$