Cho tứ giác ABCD , AB song song CD góc A = góc 3D , góc B – góc C = 30 độ
Tính góc A , B , C , D
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
(2\(x\) + 1)3
= (2\(x\))3 + 3.(2\(x\))2 + 3.2\(x\).12 + 13
= 8\(x^3\) + 12\(x^2\) + 6\(x\) + 1
ND
16 tháng 8 2023
Mày ra câu hỏi từ từ người ta trả lới cho chứ cứ hối người ta 😡
CC
3
CC
2
CC
0
16 tháng 8 2023
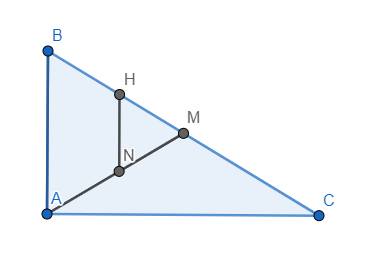
Ta có \(HN\perp AC\) và \(AB\perp AC\) nên AB//HN. Do đó tứ giác ABHN là hình thang (1)
Mặt khác, tam giác ABC vuông tại A có trung tuyến AM nên \(AM=\dfrac{1}{2}BC=BM\), suy ra tam giác MAB cân tại M hay \(\widehat{ABH}=\widehat{NAB}\) (2)
Từ (1) và (2), ta suy ra tứ giác ABHN là hình thang cân. (đpcm)
Vì AB//CD nên Góc A và góc D là hai góc trong cùng phía
\(\widehat{A}\)+ \(\widehat{D}\) = 1800 ⇒ \(\widehat{D}\) + 3\(\widehat{D}\) = 1800 ⇒ \(\widehat{D}\) = 1800:4 = 450
\(\widehat{A}\) = 450.3 =1350
\(\widehat{B}\)+\(\widehat{C}\) = 1800 ⇒ \(\widehat{B}\) + \(\widehat{B}\) - 300 = 1800 ⇒2\(\widehat{B}\) =2100 ⇒ \(\widehat{B}\) = 1050
\(\widehat{C}\) = 1050 - 300 = 750