Một hộp đựng 15 tấm thẻ giống nhau được đánh số 1; 2;3 ; ...; 15 Bạn Lan rút ngẫu nhiên một tấm thẻ trong hộc ,Tính xác suất của các biến cố sau:
a) E: " Rút được tấm thẻ ghi số chia hết cho 3 "
b) G: " Rút được tấm thẻ ghi số nguyên tố "
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\left(a^2+b^2+c^2\right)=a^4+b^4+c^4+2a^2b^2+2b^2c^2+2c^2a^2\) (1)
Lại có: \(a+b+c=0\)
\(\Leftrightarrow\left(a+b+c\right)^2=0\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ca=0\)
\(\Leftrightarrow a^2+b^2+c^2=-2\left(ab+bc+ca\right)\)
\(\Leftrightarrow\left(a^2+b^2+c^2\right)^2=\left[-2\left(ab+bc+ca\right)\right]^2=4\left[a^2b^2+b^2c^2+c^2a^2+2abc\left(a+b+c\right)\right]\)
\(=4a^2b^2+4b^2c^2+4c^2a^2=2\left(2a^2b^2+2b^2c^2+2c^2a^2\right)\) (2)
Từ (1) và (2) \(\Rightarrow a^4+b^4+c^4=2a^2b^2+2b^2c^2+2c^2a^2=\dfrac{\left(a^2+b^2+c^2\right)^2}{2}\) (đpcm)

Lời giải:
$a^2+b^2<2$
$\Leftrightarrow (a-b)^2+2ab<2$
$\Leftrightarrow ab< \frac{2-(a-b)^2}{2}\leq \frac{2}{2}=1$
BĐT cần chứng minh tương đương với:
$\frac{a^2+b^2+2}{(a^2+1)(b^2+1)}\leq \frac{2}{1+ab}$
$\Leftrightarrow (a^2+b^2+2)(1+ab)\leq 2(a^2+1)(b^2+1)$
$\Leftrightarrow a^2+b^2+2+ab(a^2+b^2+2)\leq 2(a^2b^2+a^2+b^2+1)$
$\Leftrightarrow ab(a^2+b^2+2)\leq 2a^2b^2+a^2+b^2$
$\Leftrightarrow ab(a^2+b^2-2ab)-(a^2+b^2-2ab)\leq 0$
$\Leftrightarrow ab(a-b)^2-(a-b)^2\leq 0$
$\Leftrightarrow (a-b)^2(ab-1)\leq 0$ (luôn đúng với mọi $a,b\in\mathbb{R}$ và $ab<1$)
Do đó ta có đpcm.

a: Xét ΔBHE vuông tại E và ΔCHF vuông tại F có
\(\widehat{BHE}=\widehat{CHF}\)(hai góc đối đỉnh)
Do đó; ΔBHE~ΔCHF
b: Xét ΔAEH vuông tại E và ΔADB vuông tại D có
\(\widehat{EAH}\) chung
Do đó: ΔAEH~ΔADB
=>\(\dfrac{AE}{AD}=\dfrac{AH}{AB}\)
=>\(AE\cdot AB=AH\cdot AD\)
c: Xét ΔAFB vuông tại F và ΔAEC vuông tại E có
\(\widehat{FAB}\) chung
Do đó: ΔAFB~ΔAEC
=>\(\dfrac{AF}{AE}=\dfrac{AB}{AC}\)
=>\(\dfrac{AF}{AB}=\dfrac{AE}{AC}\)
Xét ΔAFE và ΔABC có
\(\dfrac{AF}{AB}=\dfrac{AE}{AC}\)
Do đó: ΔAFE~ΔABC
=>\(\dfrac{AF}{AB}=\dfrac{AE}{AC}\)
\(\left(\dfrac{AF}{AB}\right)^2=\dfrac{1}{2}\)
=>\(\dfrac{AF}{AB}=\dfrac{\sqrt{2}}{2}=\dfrac{AE}{AC}\)
Xét ΔAEC vuông tại E có \(sinACE=\dfrac{AE}{AC}=\dfrac{\sqrt{2}}{2}\)
nên \(\widehat{ACE}=45^0\)
=>\(\widehat{ABF}=45^0\)
Xét tứ giác BEHD có \(\widehat{BEH}+\widehat{BDH}=90^0+90^0=180^0\)
nên BEHD là tứ giác nội tiếp
=>\(\widehat{EDH}=\widehat{EBH}=45^0\)
Xét tứ giác DCFH có \(\widehat{HDC}+\widehat{HFC}=90^0+90^0=180^0\)
nên DCFH là tứ giác nội tiếp
=>\(\widehat{HDF}=\widehat{HCF}=45^0\)
\(\widehat{EDF}=\widehat{EDH}+\widehat{FDH}=45^0+45^0=90^0\)
=>ΔEDF vuông tại D

a: \(\dfrac{x-1}{4}-\dfrac{3x}{2}=1+\dfrac{2x-1}{3}\)
=>\(\dfrac{x-1-6x}{4}=\dfrac{3+2x-1}{3}\)
=>\(\dfrac{-5x-1}{4}=\dfrac{2x+2}{3}\)
=>\(4\left(2x+2\right)=3\left(-5x-1\right)\)
=>-15x-3=8x+8
=>-23x=11
=>\(x=-\dfrac{11}{23}\)
b: \(\left(4x-1\right)\left(x+5\right)=x^2-25\)
=>\(\left(4x-1\right)\left(x+5\right)-\left(x-5\right)\left(x+5\right)=0\)
=>\(\left(x+5\right)\left(4x-1-x+5\right)=0\)
=>(x+5)(3x+4)=0
=>\(\left[{}\begin{matrix}x=-5\\x=-\dfrac{4}{3}\end{matrix}\right.\)
c: \(x\left(x-1\right)\left(x^2-x+1\right)-6=0\)
=>\(\left(x^2-x\right)\left(x^2-x+1\right)-6=0\)
=>\(\left(x^2-x\right)^2+\left(x^2-x\right)-6=0\)
=>\(\left(x^2-x+3\right)\left(x^2-x-2\right)=0\)
mà \(x^2-x+3=\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall x\)
nên \(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)

a: Thay x=5 vào A, ta được:
\(A=\dfrac{5+3}{5^2}=\dfrac{8}{25}\)
b: \(B=\dfrac{x-6}{x^2-4}+\dfrac{3}{x-2}+\dfrac{x}{x+2}\)
\(=\dfrac{x-6}{\left(x-2\right)\left(x+2\right)}+\dfrac{3}{x-2}+\dfrac{x}{x+2}\)
\(=\dfrac{x-6+3\left(x+2\right)+x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x-6+3x+6+x^2-2x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+2x}{\left(x-2\right)\left(x+2\right)}=\dfrac{x}{x-2}\)
c: \(P=A\cdot B=\dfrac{x}{x-2}\cdot\dfrac{x+3}{x^2}=\dfrac{x+3}{x\left(x-2\right)}\)
\(P=\dfrac{1}{x+2}\)
=>\(\dfrac{x+3}{x\left(x-2\right)}=\dfrac{1}{x+2}\)
=>\(x\left(x-2\right)=\left(x+3\right)\left(x+2\right)\)
=>\(x^2+5x+6=x^2-2x\)
=>7x=-6
=>\(x=-\dfrac{6}{7}\left(nhận\right)\)

a: \(3x\left(x-7\right)+2xy-14y\)
\(=3x\left(x-7\right)+2y\left(x-7\right)\)
=(x-7)(3x+2y)
b: \(\left(4x-y\right)\left(a+b\right)-\left(y-4x\right)\left(b-1\right)\)
\(=\left(4x-y\right)\left(a+b\right)+\left(4x-y\right)\left(b-1\right)\)
\(=\left(4x-y\right)\left(a+b+b-1\right)\)
\(=\left(4x-y\right)\left(a+2b-1\right)\)
c: \(2x^2-x-6xy+3y\)
\(=\left(2x^2-x\right)-\left(6xy-3y\right)\)
\(=x\left(2x-1\right)-3y\left(2x-1\right)\)
\(=\left(2x-1\right)\left(x-3y\right)\)
d: \(x^2-z^2+4xy+4y^2\)
\(=\left(x^2+4xy+4y^2\right)-z^2\)
\(=\left(x+2y\right)^2-z^2\)
\(=\left(x+2y+z\right)\left(x+2y-z\right)\)

a: \(\left(2-3x\right)^2-5x\left(x-4\right)+4\left(x-1\right)\)
\(=9x^2-12x+4-5x^2+20x+4x-4\)
\(=4x^2+12x\)
b: \(\left(x-1\right)^2-2\left(x-1\right)\left(x+2\right)+\left(x+2\right)^2+5\left(2x-3\right)\)
\(=x^2-2x+1-2\left(x^2+x-2\right)+x^2+4x+4+10x-15\)
\(=2x^2+12x-14-2x^2-2x+4\)
=10x-10
c: \(\left(x-2\right)^3-6\left(x+4\right)\left(x-4\right)-\left(x-2\right)\left(x^2+2x+4\right)\)
\(=x^3-6x^2+12x-8-\left(x^3-8\right)-6\left(x^2-16\right)\)
\(=x^3-6x^2+12x-8-x^3+8-6x^2+96\)
\(=-12x^2+12x+96\)

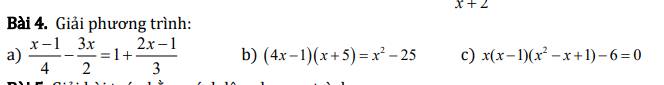


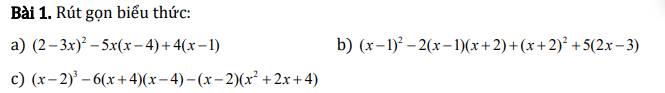
a) Có 5 tấm thẻ ghi số chia hết cho 5 có thể rút được là: \(3;6;9;12;15\)
Xác suất của biến cố E là:
\(P\left(E\right)=\dfrac{5}{15}=\dfrac{1}{3}\)
b) Có 6 tấm thẻ ghi số nguyên tố có thể rút được là: \(2;3;5;7;11;13\)
Xác suất của biến cố G là:
\(P\left(G\right)=\dfrac{6}{15}=\dfrac{2}{5}\)
a)Có 5 thuận lại cho biến cố E là: 3;6;9;12;15
Xác suất của biến cố E là:
\(\dfrac{5}{15}=\dfrac{1}{3}\)
b)Có 6 thuận lại cho biến cố E là: 2;3;5;7;11;13
Xác suất của biến cố G là:
\(\dfrac{6}{15}=\dfrac{2}{5}\)