Để A có giá trị là một số nguyên thì:

\(\left(\sqrt{x}+1\right)⋮\left(\sqrt{x}-3\right)\)

\(\Leftrightarrow\left(\sqrt{x}-3\right)+4⋮\left(\sqrt{x}-3\right)\)

\(\Leftrightarrow4⋮\left(\sqrt{x}-3\right)\)

Vì \(x\in Z\) nên \(\left(\sqrt{x}-3\right)\inƯ\left(4\right)=\left\{\pm1,\pm2,\pm4\right\}\)

Ta có bảng sau:

Vậy ....

Ta có: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\left(\sqrt{x}-3\right)+4}{\sqrt{x}-3}=\dfrac{\sqrt{x}-3}{\sqrt{x}-3}=\dfrac{4}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\)

Để A có giá trị là một số nguyên khi:

\(4⋮\sqrt{x}-3\) hay \(\sqrt{x}-3\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)

Do đó:

\(\sqrt{x}-3=-1\Rightarrow\sqrt{x}=-1+3=2\Rightarrow x=4\)

\(\sqrt{x}-3=1\Rightarrow\sqrt{x}=1+3=4\Rightarrow x=16\)

\(\sqrt{x}-3=-2\Rightarrow\sqrt{x}=-2+3=1\Rightarrow x=1\)

\(\sqrt{x}-3=2\Rightarrow\sqrt{x}=2+3=5\Rightarrow x=25\)

\(\sqrt{x}-3=-4\Rightarrow\sqrt{x}=-4+3=-1\)  ( loại )

\(\sqrt{x}-3=4\Rightarrow\sqrt{x}=4+3=7\Rightarrow x=49\)

Vậy để A là một số nguyên khi \(x\in\left\{4;16;1;25;49\right\}\)

Lời giải:
$\frac{55-x}{1963}+\frac{50-x}{1968}+\frac{45-x}{1973}+\frac{40-x}{1978}+4=0$

$\frac{55-x}{1963}+1+\frac{50-x}{1968}+1+\frac{45-x}{1973}+1+\frac{40-x}{1978}+1=0$

$\frac{2018-x}{1963}+\frac{2018-x}{1968}+\frac{2018-x}{1973}+\frac{2018-x}{1978}=0$

$(2018-x)(\frac{1}{1963}+\frac{1}{1968}+\frac{1}{1973}+\frac{1}{1978})=0$

$\Rightarrow 2018-x=0$

$\Rightarrow x=2018$.

=1

Lời giải:
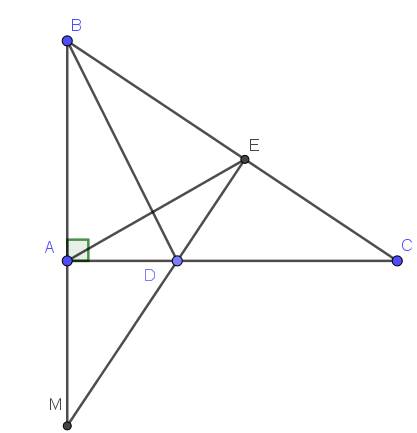
a. Xét tam giác $ABD$ và $EBD$ có:

$AB=EB$ 

$BD$ chung

$\widehat{ABD}=\widehat{EBD}$ (do $BD$ là phân giác $\widehat{B}$)

$\Rightarrow \triangle ABD=\triangle EBD$ (c.g.c)

b.

Từ tam giác bằng nhau phần a suy ra:

$AD=DE$

$\widehat{BED}=\widehat{BAD}=90^0$

$\Rightarrow DE\perp BC$

$\Rightarrow \widehat{DEC}=90^0$
Xét tam giác $ADM$ và $EDC$ có:

$AD=ED$ (cmt)

$\widehat{ADM}=\widehat{EDC}$ (đối đỉnh)

$\widehat{DAM}=\widehat{DEC}=90^0$

$\Rightarrow \triangle ADM=\triangle EDC$ (g.c.g)

$\Rightarrow AM=EC$

c.

Từ tam giác bằng nhau phần b suy ra:

$\widehat{M_1}=\widehat{C_1}$

$DM=DC$

Mà $DE=AD$

$\Rightarrow DM+DE=DC+AD$

$\Rightarrow ME=AC$

Xét tam giác $AEM$ và $EAC$ có:

$AM=EC$ (cmt)

$EM=AC$ (cmt)

$\widehat{M_1}=\widehat{C_1}$ (cmt)

$\Rightarrow \triangle AEM=\triangle EAC$ (c.g.c)

$\Rightarrow \widehat{EAM}=\widehat{AEC}$

Hình vẽ:

C đúng 

Số đối của số hữu tỉ - \(\dfrac{22}{23}\) là \(\dfrac{22}{23}\)

Số đối của số hữu tỉ trên là : \(\dfrac{22}{23}\)