Tập hợp bội của 60 gồm 11 số là:

B(60) = {0; 60; 120; 180; 240; 300; 360; 420; 480; 540; 600}

B(60)={0,60,120,180,240,300,360,

...

a) Ta có:

\( A = 5+5^2+5^3+\ldots+5^{100} \)

Để chứng minh A chia hết cho 5, ta xét tổng S = \( 5+5^2+5^3+\ldots+5^{100} \) (mod 5).

Ta thấy rằng \( 5 \) chia hết cho 5, \( 5^2 \) chia hết cho 5, \( 5^3 \) chia hết cho 5, và tiếp tục như vậy cho tới \( 5^{100} \).

Vì vậy, ta có: \( S \equiv 0+0+0+\ldots+0 \equiv 0 \) (mod 5).

Do đó, A chia hết cho 5.

Để chứng minh A không chia hết cho 25, ta xét tổng T = \( 5+5^2+5^3+\ldots+5^{100} \) (mod 25).

Ta thấy rằng \( 5 \) không chia hết cho 25, \( 5^2 \) không chia hết cho 25, \( 5^3 \) không chia hết cho 25, và tiếp tục như vậy cho tới \( 5^{100} \).

Vì vậy, ta có: \( T \equiv 5+0+0+\ldots+0 \equiv 5 \) (mod 25).

Do đó, A không chia hết cho 25.

b) Ta có:

\( B = 5+5^2+5^3+\ldots+5^{20} \)

Để chứng minh B chia hết cho 6, ta xét tổng U = \( 5+5^2+5^3+\ldots+5^{20} \) (mod 6).

Ta thấy rằng \( 5 \) chia hết cho 6, \( 5^2 \) không chia hết cho 6, \( 5^3 \) không chia hết cho 6, \( 5^4 \) chia hết cho 6, và tiếp tục như vậy cho tới \( 5^{20} \).

Vì vậy, ta có: \( U \equiv 5+1+1+\ldots+1 \equiv 5 \) (mod 6).

Do đó, B chia hết cho 6.

c) Ta có:

\( C = 5+5^2+5^3+\ldots+5^{2022}+5^{2023} \)

Để chứng minh C không chia hết cho 6, ta xét tổng V = \( 5+5^2+5^3+\ldots+5^{2022}+5^{2023} \) (mod 6).

Ta thấy rằng \( 5 \) chia hết cho 6, \( 5^2 \) không chia hết cho 6, \( 5^3 \) không chia hết cho 6, \( 5^4 \) chia hết cho 6, và tiếp tục như vậy cho tới \( 5^{2022} \) và \( 5^{2023} \).

Vì vậy, ta có: \( V \equiv 5+1+1+\ldots+1 \equiv 2 \) (mod 6).

Do đó, C không chia hết cho 6.

d) Ta có:

\( D = 1+2+2^2+2^3+\ldots+2^{2021} \)

Để chứng minh D chia hết cho 7, ta xét tổng W = \( 1+2+2^2+2^3+\ldots+2^{2021} \) (mod 7).

Ta thấy rằng \( 2 \) không chia hết cho 7, \( 2^2 \) chia hết cho 7, \( 2^3 \) không chia hết cho 7, \( 2^4 \) không chia hết cho 7, \( 2^5 \) không chia hết cho 7, \( 2^6 \) chia hết cho 7, và tiếp tục

mong mn cho minh vai xu :)))))))))))))))))))))))))))))))))

bạn Tiến Dũng Trương lm sai r

Lời giải:
$A=(1+2)+(2^2+2^3)+.....+(2^{10}+2^{11})$

$=(1+2)+2^2(1+2)+...+2^{10}(1+2)$
$=(1+2)(1+2^2+....+2^{10})$

$=3(1+2^2+....+2^{10})\vdots 3$ (đpcm)

A = 1 + 2 + 2² + 2³ + ... + 2¹¹

A = 2⁰ + 2¹ + 2² + 2³ + ... + 2¹¹

Xét dãy số: 0; 1; 2; 3;...;11 dãy số này là dãy số cách đều với khoảng cách là: 1 - 0 = 1

Số số hạng của dãy số trên là: (11 - 10) : 1 + 1 = 12 (số hạng)

Vậy A có 12 hang tử nhóm hai hạng tử liên tiếp của A với nhau vì  

12 : 2 = 6 nên:

A = (1 + 2) + ( 2² + 2³) +...+ (2¹⁰ + 2¹¹)

A = 3 + 2².(1 + 2) + ...+ 2¹⁰.(1 + 2)

A = 3 + 2². 3 +...+ 2¹⁰.3

A = 3.( 1 + 2² +...+ 2¹⁰)

vì 3 ⋮ 3 nên 3.(1 + 2² + ...+ 2¹⁰) ⋮ 3 hay A = 1 + 2+ ...+ 2¹¹ ⋮ 3(đpcm)

Lời giải:
Nếu $a\vdots 3$. Đặt $a=3k$ với $k$ tự nhiên.

Khi đó: $a+15=3k+15=3(k+5)\vdots 3$

$\Rightarrow M=(a+15)(a+17)(4a+1)\vdots 3$

Nếu $a$ chia $3$ dư $1$. Đặt $a=3k+1$ với $k$ tự nhiên.

Khi đó: $a+17=3k+1+17=3k+18=3(k+6)\vdots 3$

$\Rightarrow M=(a+15)(a+17)(4a+1)\vdots 3$

Nếu $a$ chia $3$ dư $2$. Đặt $a=3k+2$ với $k$ tự nhiên

Khi đó: $4a+1=4(3k+2)+1=12k+9=3(4k+3)\vdots 3$

$\Rightarrow M\vdots 3$

Vậy $M$ luôn chia hết cho $3$ với mọi $a$ tự nhiên.

18 = 2.3²

30 = 2.3.5

ƯCLN(18; 30) = 2.3 = 6

UC(18;30) = {1; 2; 3; 6}

18 = 2.3²

30 = 2.3.5

ƯCLN(18; 30) = 2.3 = 6

ƯC(18; 30) = Ư(6) = {1; 2; 3; 6}

36=2².3²

80=2⁴.5

ƯC(36;80)

=2²=4

nhớ tích đấy

Lời giải:

$180+24+x\vdots 9$

$\Rightarrow 9.20+9.3+x-3\vdots 9$

$\Rightarrow x-3\vdots 9$

Vậy $x$ chia $9$ dư $3$. $x$ là số tự nhiên có 2 chữ số nên:

$x\in\left\{12; 21;30;39;....; 93\right\}$

Phần diện tích tăng thêm bằng với diện tích hình chữ nhật có chiều dài là 25m, rộng 10 m mới đúng đề bài chứ em

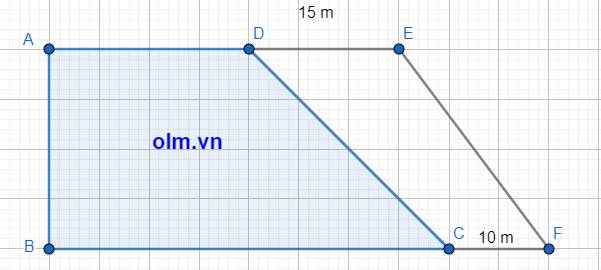
Diện tích hình chữ nhật là: 25 x 10 = 250 (m²)

Chiều cao của hình thang là: 250 x 2: (15+10) = 20(m)

Tổng độ dài của đáy bé và đáy lớn hình thang ban đầu là:

            600 x 2 : 20 = 60 (m)

Gọi đáy bé của thủa ruộng ban đầu là \(x\) (m) ; \(x\) > 0

Thì đáy lớn của thửa rộng ban đầu là: \(x\) + 24 (m)

Theo bài ra ta có: \(x\) + 24 + \(x\) = 60

                             2\(x\) + 24 = 60

                            2\(x\)          = 60 - 24

                            2\(x\)          = 36

                             \(x\)            = 36 : 2

                              \(x\)           = 18 (m)

Đáy lớn của thửa ruộng ban đầu là:

                             18 +  24 = 42 (m)

Kết luận:...