$B=1+2+3+4+...+2022+2023$

Số các số hạng của B là:

$(2023-1):1+1=2023$ (số)

Tổng B bằng:

$(2023+1)\cdot2023:2=2047276$

$---$

$C=2+4+6+...+98+100$

Số các số hạng của C là:

$(100-2):2+1=50$ (số)

Tổng C bằng:

$(100+2)\cdot50:2=2550$

$---$

$D=1+3+5+...+97+99$

Số các số hạng của D là:

$(99-1):2+1=50$ (số)

Tổng D bằng:

$(99+1)\cdot50:2=2500$

$---$

$E=10+14+18+...+98+102$

Số các số hạng của E là:

$(102-10):4+1=24$ (số)

Tổng E bằng:

$(102+10)\cdot24:2=1344$

$Toru$

Số lượng số hạng: 

\(\left(2023-1\right):1+1=2023\) (số hạng) 

Tổng B là:

\(B=\left(2023+1\right)\cdot2023:2=2047276\)

_______________

Số lượng số hạng là:

\(\left(100-2\right):2+1=50\) (số hạng)

Tổng C là: 

\(C=\left(100+2\right)\cdot50:2=2550\)

________________

Số lượng số hạng là:

\(\left(99-1\right):2+1=50\) (số hạng)

Tổng D là:

\(D=\left(99+1\right)\cdot50:2=2500\) 

________________

Số lượng số hạng là:

\(\left(102-10\right):4+1=24\) (số hạng)

Tổng E là:

\(E=\left(102+10\right)\cdot24:2=1334\)  

Bạn lưu ý khi đăng câu hỏi thì đăng đầy đủ đề, kèm theo điều kiện của $x,y$.

Trong bài này mình giả sử $x,y$ là các số nguyên.

Tìm $x,y$ thỏa mãn: $(x+3)+y(x+2)=17$

--------------------------

Lời giải:
$(x+3)+y(x+2)=17$

$(x+2)+y(x+2)=16$

$(x+2)(y+1)=16$

Vì $x+2, y+1$ là các số nguyên với mọi $x,y$ nguyên nên ta có bảng sau:

b sai

6:2(1+2)=6:2.3

               =3.3

               =9

6 : 2 x (1 + 2)

= 3 x 3

= 9.

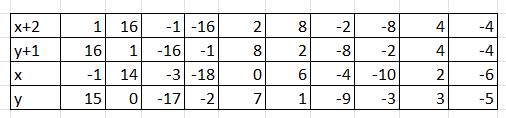
Dùng phương pháp xét tính chẵn lẻ em nhé

Với n là số tự nhiên ta có: n + 7 - (n + 4) = 3 (là số lẻ)

Vậy n + 7 và n + 4 khác tính chẵn lẻ hay một trong hai số phải có một số là số chẵn và một số là số lẻ. Mà số chẵn thì luôn chia hết cho 2

Vậy (n +4).(n +7) ⋮ 2 ∀ n \(\in\) N

Vậy (n +4).(n +7) ⋮ 2 ∀ n $\in$ N

C1:20+5=25

C2:10+10+5=25

C3:10+5+5+5=25

C4:5+5+5+5+5

nhớ tick nhé bạn iu

\(S=1+2^2+2^4+2^6+2^8+...+2^{2024}\\2^2\cdot S=2^2\cdot(1+2^2+2^4+2^6+2^8+...+2^{2024})\\4S=2^2+2^4+2^6+2^8+2^{10}+...+2^{2026}\\4S-S=(2^2+2^4+2^6+2^8+2^{10}+...+2^{2026})-(1+2^2+2^4+2^6+2^8+...+2^{2024})\\3S=2^{2026}-1\\\Rightarrow S=\dfrac{2^{2026}-1}{3}\\Toru\)

hi ngọc nhé =) bít nek

\(3^6:x=3^2.3^3\)

\(3^6:x=3^5\)

\(x=3^6:3^5\)

\(x=3\)

3 mũ 6 : x = 3².3³

3 mũ 6 : x = 3 mũ 5

X= 3 mũ 6 : 3 mũ 5

X=3

ta có 

abcd

= ab. 100 + cd

=8cd . 100 + cd

= cd ( 100.8 + 1)

= cd .801

mà 801 ⋮ 89 

=. cd. 801 ⋮ 89

=> abcd ⋮ 89

\(\overline{abcd}\) = \(\overline{ab}\) x 100 + \(\overline{cd}\) 

Thay \(\overline{ab}\) = 8.\(\overline{cd}\) vào biểu thức: \(\overline{abcd}\) = \(\overline{ab}\) x 100 + \(\overline{cd}\) ta có: 

\(\overline{abcd}\) = 8.\(\overline{cd}\).100 + \(\overline{cd}\)

\(\overline{abcd}\) = 801.\(\overline{cd}\) = 89.9.\(\overline{cd}\) ⋮ 89 (đpcm)