Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`#3107.101107`
`a,`
`x - 315 =121 + 89`
`x - 315 = 210`
`x = 210 + 315`
`x = 525`
Vậy, `x = 525`
`b,`
`x + 326 = 558 - 18`
`x + 326 = 540`
`x = 540 - 326`
`x = 214`
Vậy, `x = 214`
`c,`
`x \times 4 = 21 + 15`
`x \times 4 = 36`
`x = 36 \div 4`
`x = 9`
Vậy, `x = 9`
`d,`
`x \div 5 = 108 - 99`
`x \div 5 = 9`
`x = 9 \times 5`
`x = 45`
Vậy, `x = 45.`
a) x - 315 = 121 + 89
x - 315 = 210
x = 210 + 315
x = 525
b) x + 326 = 558 - 18
x + 326 = 540
x = 540 - 326
x = 214
c)
\(x\times4=21+15\\ x\times4=36\\ x=36:4\\ x=9\)
d)
\(x:5=108-99\\ x:5=9\\ x=5\times9\\ x=45\)

b) Để ý rằng phương trình của trục Ox là \(y=0\). Do đó pt hoành độ giao điểm của Ox và d là \(\left(m^2+1\right)x_A-2m=0\Leftrightarrow x_A=\dfrac{2m}{m^2+1}\)
Mà \(OA=\left|x_A\right|=\left|\dfrac{2m}{m^2+1}\right|=\dfrac{2\left|m\right|}{m^2+1}\) , \(OA=\dfrac{4}{5}\)
\(\Rightarrow\dfrac{2\left|m\right|}{m^2+1}=\dfrac{4}{5}\)
\(\Leftrightarrow2m^2-5\left|m\right|+2=0\)
Xét \(m\ge0\), khi đó \(2m^2-5m+2=0\Leftrightarrow\left[{}\begin{matrix}m=2\\m=\dfrac{1}{2}\end{matrix}\right.\) (nhận)
Xét \(m< 0\), khi đó \(2m^2+5m+2=0\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{1}{2}\\m=-2\end{matrix}\right.\) (nhận)
Vậy \(m\in\left\{\pm2;\pm\dfrac{1}{2}\right\}\) thỏa mãn ycbt.
c) Theo câu b), ta có \(OA=\dfrac{2\left|m\right|}{m^2+1}\). d cắt Oy tại \(B\left(0,-2m\right)\)
\(\Rightarrow OB=\left|-2m\right|=2\left|m\right|\)
Có \(OA=2OB\Leftrightarrow\dfrac{2\left|m\right|}{m^2+1}=4\left|m\right|\)
\(\Leftrightarrow\left|m\right|\left(2-\dfrac{1}{m^2+1}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\2m^2+1=0\left(vôlý\right)\end{matrix}\right.\)
Vậy \(m=0\) thỏa mãn ycbt.
d) Gọi \(h\) là khoảng cách từ O đến d thì khi đó:
\(\dfrac{1}{h^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\)
\(=\dfrac{1}{\left(\dfrac{2\left|m\right|}{m^2+1}\right)^2}+\dfrac{1}{\left(2\left|m\right|\right)^2}\)
\(=\dfrac{m^4+2m^2+1}{4m^2}+\dfrac{1}{4m^2}\)
\(=\dfrac{m^4+2m^2+2}{4m^2}\)
\(\Rightarrow h^2=\dfrac{4m^2}{m^4+2m^2+2}\)
Đặt \(t=m^2\left(t>0\right)\) thì ta có \(h^2=\dfrac{4t}{t^2+2t+2}=P\)
\(\Leftrightarrow Pt^2+2\left(P-2\right)t+2P=0\) (*)
Có \(\Delta'=\left(P-2\right)^2-2P^2=P^2-4P+4-2P^2=-P^2-4P+4\)
\(\Delta'\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Ta thấy \(P=\dfrac{2P}{P}=2>0\) nên để pt đã cho có 1 nghiệm dương thì \(S>0\Leftrightarrow-2\left(P-2\right)>0\Leftrightarrow P< 2\)
Kết hợp 2 điều kiện, ta được \(-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Vậy \(maxP=-2+2\sqrt{2}\). Dấu "=" xảy ra khi \(t=\dfrac{-2\left(-2+2\sqrt{2}-2\right)}{2\left(-2+2\sqrt{2}\right)}=\sqrt{2}\)
\(\Leftrightarrow m^2=\sqrt{2}\Leftrightarrow m=\pm\sqrt[4]{2}\)
Vậy \(m=\pm\sqrt[4]{2}\) thỏa mãn ycbt.

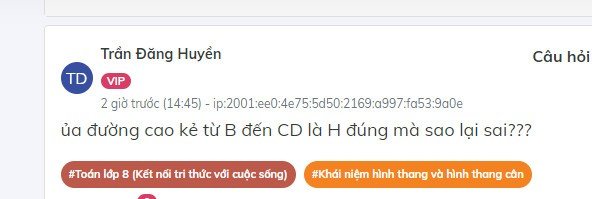
Em ghi là đường cao H là sai, phải ghi là BH mới đúng vì vậy Olm bảo em làm sai em hiểu chưa nhỉ?

Bài 1:
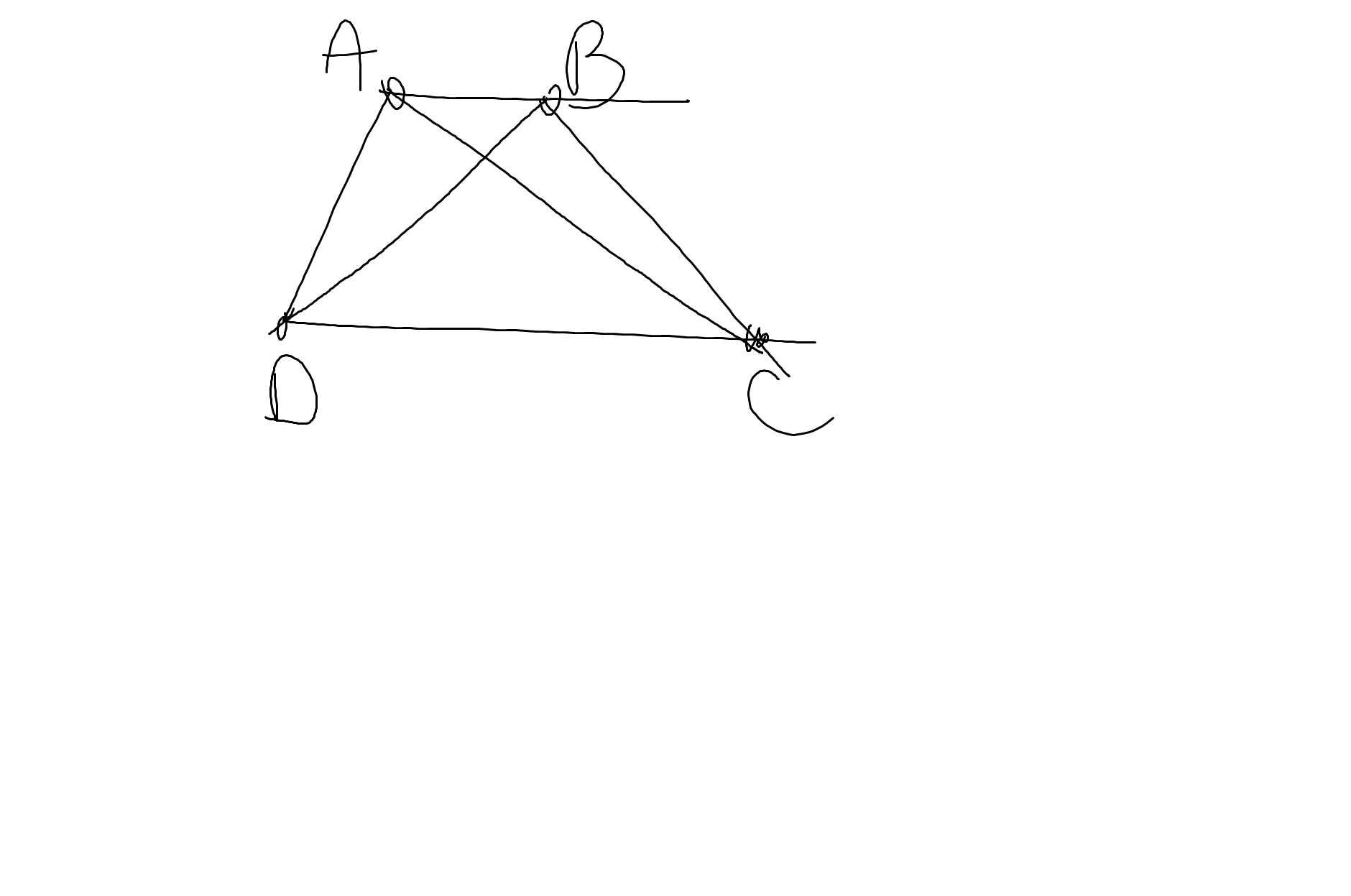
a: Hai cạnh đáy là AB,CD
Hai cạnh bên là AD,BC
b: Các cặp góc kề cạnh đáy là:
\(\widehat{BAD};\widehat{ABC}\)
\(\widehat{ADC};\widehat{BCD}\)
Các cặp góc kề cạnh bên là:
\(\widehat{BAD};\widehat{ADC}\)
\(\widehat{ABC};\widehat{BCD}\)
c: Hai đường chéo là AC,BD
Bài 2:
a: Ta có: ΔDAC vuông cân tại D
=>\(\widehat{DAC}=\widehat{DCA}=45^0\)
Ta có: ΔABC vuông cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=45^0\)
Ta có: \(\widehat{DAC}=\widehat{ACB}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//CB
=>ABCD là hình thang
Hình thang ABCD có AD\(\perp\)DC
nên ABCD là hình thang vuông
b: ABCD là hình thang vuông có hai đáy là AD,CB và AD\(\perp\)DC
=>CB\(\perp\)CD
=>\(\widehat{ADC}=\widehat{DCB}=90^0\)
Ta có: AD//CB
=>\(\widehat{DAB}+\widehat{ABC}=180^0\)
=>\(\widehat{DAB}=180^0-45^0=135^0\)

\(1+3+5+...+x=36\\\left[ \left(x-1\right):2+1\right]\cdot\left(x+1\right):2=36\\ \dfrac{x-1+2}{2}\cdot\dfrac{x+1}{2}=36\\ \dfrac{x+1}{2}\cdot\dfrac{x+1}{2}=36\\ \dfrac{\left(x+1\right)^2}{4}=36\\ \left(x+1\right)^2=36\cdot4=144\)
TH1: x + 1 = 12 => x = 11
TH2: x + 1 = -12 => x = -13
Vì: x phải lớn hơn 0 => x = 11

Bài 1:
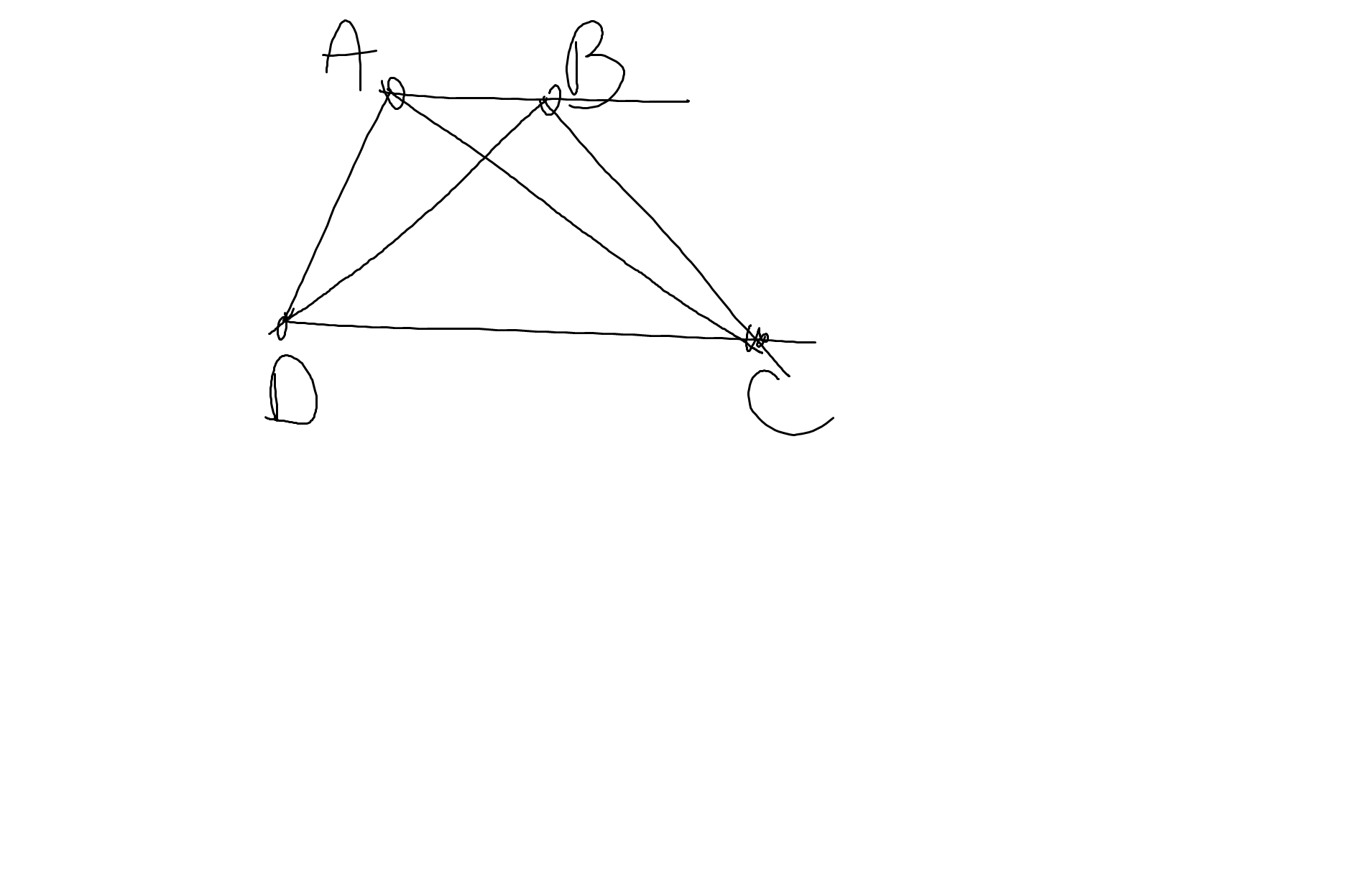
a: Hai cạnh đáy là AB,CD
Hai cạnh bên là AD,BC
b: Các cặp góc kề cạnh đáy là:
\(\widehat{BAD};\widehat{ABC}\)
\(\widehat{ADC};\widehat{BCD}\)
Các cặp góc kề cạnh bên là:
\(\widehat{BAD};\widehat{ADC}\)
\(\widehat{ABC};\widehat{BCD}\)
c: Hai đường chéo là AC,BD
Bài 2:
a: Ta có: ΔDAC vuông cân tại D
=>\(\widehat{DAC}=\widehat{DCA}=45^0\)
Ta có: ΔABC vuông cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=45^0\)
Ta có: \(\widehat{DAC}=\widehat{ACB}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//CB
=>ABCD là hình thang
Hình thang ABCD có AD\(\perp\)DC
nên ABCD là hình thang vuông
b: ABCD là hình thang vuông có hai đáy là AD,CB và AD\(\perp\)DC
=>CB\(\perp\)CD
=>\(\widehat{ADC}=\widehat{DCB}=90^0\)
Ta có: AD//CB
=>\(\widehat{DAB}+\widehat{ABC}=180^0\)
=>\(\widehat{DAB}=180^0-45^0=135^0\)


a)
\(\dfrac{8}{9}-\dfrac{1}{72}-\dfrac{1}{56}-\dfrac{1}{42}-\dfrac{1}{30}-\dfrac{1}{20}-\dfrac{1}{12}-\dfrac{1}{6}-\dfrac{1}{2}\\ =\dfrac{8}{9}-\left(\dfrac{1}{72}+\dfrac{1}{56}+\dfrac{1}{42}+\dfrac{1}{30}+\dfrac{1}{20}+\dfrac{1}{12}+\dfrac{1}{6}+\dfrac{1}{2}\right)\\ =\dfrac{8}{9}-\left(\dfrac{1}{8\cdot9}+\dfrac{1}{7\cdot8}+\dfrac{1}{6\cdot7}+\dfrac{1}{6\cdot5}+\dfrac{1}{4\cdot5}+\dfrac{1}{3\cdot4}+\dfrac{1}{2\cdot3}+\dfrac{1}{1\cdot2}\right)\\ =\dfrac{8}{9}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}\right)\\ =\dfrac{8}{9}-\left(1-\dfrac{1}{9}\right)\\ =\dfrac{8}{9}-\dfrac{8}{9}\\ =0\)
b)
\(\left(-\dfrac{1}{2}\right)-\left(\dfrac{-3}{5}\right)+\left(-\dfrac{1}{9}\right)+\dfrac{1}{127}-\dfrac{7}{18}+\dfrac{4}{35}-\left(\dfrac{-2}{7}\right)\\ =\left(-\dfrac{1}{2}-\dfrac{1}{9}-\dfrac{7}{18}\right)+\left(\dfrac{3}{5}+\dfrac{2}{7}+\dfrac{4}{35}\right)+\dfrac{1}{127}\\ =\dfrac{-9-2-7}{18}+\dfrac{21+10+4}{35}+\dfrac{1}{127}\\ =-1+1+\dfrac{1}{127}\\ =\dfrac{1}{127}\)
c) (*sửa*)
\(\dfrac{3}{5}+\dfrac{3}{11}-\dfrac{-3}{7}+\dfrac{2}{97}-\dfrac{1}{35}-\dfrac{3}{4}-\dfrac{23}{44}\\ =\dfrac{3}{5}+\dfrac{3}{11}+\dfrac{3}{7}+\dfrac{2}{97}-\dfrac{1}{35}-\dfrac{3}{4}+\dfrac{23}{44}\\ =\left(\dfrac{3}{5}+\dfrac{3}{7}-\dfrac{1}{35}\right)+\left(\dfrac{3}{11}-\dfrac{3}{4}-\dfrac{23}{44}\right)+\dfrac{2}{97}\\ =\dfrac{21+15-1}{35}+\dfrac{12-33-23}{44}+\dfrac{2}{97}\\ =1+\left(-1\right)+\dfrac{2}{97}\\ =\dfrac{2}{97}\)

\(A=2^2+2^4+2^6+...+2^{200}\\ 2^2A=2^4+2^6+...+2^{202}\\ 4A-A=\left(2^4+2^6+2^8+...+2^{202}\right)-\left(2^2+2^4+2^6+...+2^{200}\right)\\ 3A=2^{202}-2^2\)
\(=>3A+4=2^{202}-2^2+4=2^{202}-4+4=2^{202}\)
\(=>2^{202}=4^n\\ =>2^{202}=\left(2^2\right)^n\\ =>2^{202}=2^{2n}\\ =>2n=202\\ =>n=101\)

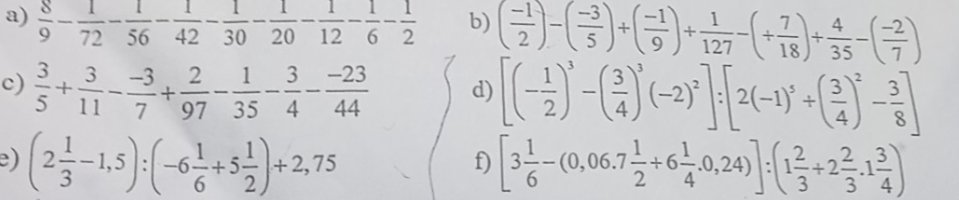
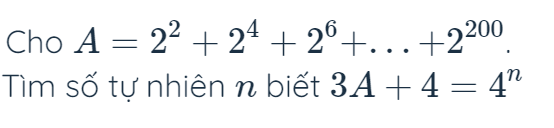
\(\left[\left(-\dfrac{1}{2}\right)^3-\left(\dfrac{3}{4}\right)^3\cdot\left(-2\right)^2\right]:\left[2\cdot\left(-1\right)^5+\left(\dfrac{3}{4}\right)^2-\dfrac{3}{8}\right]\\ =\left(-\dfrac{1}{8}-\dfrac{27}{64}\cdot4\right):\left(2\cdot-1+\dfrac{9}{16}-\dfrac{3}{8}\right)\\ =\left(-\dfrac{1}{8}-\dfrac{27}{16}\right):\left(-2+\dfrac{9}{16}-\dfrac{3}{8}\right)\\ =\left(\dfrac{-2}{16}-\dfrac{27}{16}\right):\left(\dfrac{-32}{16}+\dfrac{9}{16}-\dfrac{6}{16}\right)\\ =\dfrac{-29}{16}:\dfrac{-29}{16}\\ =1\)
____________________________
\(\left[3\dfrac{1}{6}-\left(0,06\cdot7\dfrac{1}{2}+6\dfrac{1}{4}\cdot0,24\right)\right]:\left(1\dfrac{2}{3}+2\dfrac{2}{3}\cdot1\dfrac{3}{4}\right)\\ =\left[\dfrac{19}{6}-\left(0,06\cdot\dfrac{15}{2}+\dfrac{25}{4}\cdot4\cdot0,06\right)\right]:\left(\dfrac{5}{3}+\dfrac{8}{3}\cdot\dfrac{7}{4}\right)\\ =\left[\dfrac{19}{6}-0,06\cdot\left(\dfrac{15}{4}+25\right)\right]:\left(\dfrac{5}{3}+\dfrac{14}{3}\right)\\ =\left(\dfrac{19}{6}-0,06\cdot\dfrac{65}{2}\right):\dfrac{19}{3}\\ =\left(\dfrac{19}{6}-\dfrac{39}{20}\right):\dfrac{19}{3}\\ =\dfrac{73}{60}:\dfrac{19}{3}\\ =\dfrac{73}{380}\)