Rút gọn các biểu thức sau:
\(B=x\left(x+3y+1\right)-2y\left(x-1\right)-\left(y+x+1\right)x\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Các đơn thức là :
\(\left(1-\dfrac{1}{\sqrt[]{3}}\right)x^2;x^2.\dfrac{7}{2}\)

Các đơn thức là :
\(\dfrac{x^2y}{2};\dfrac{x}{-5^2};\dfrac{-4}{5}\)

Olm chào quý thầy cô, cảm ơn quý thầy cô đã tin tưởng và sử dụng nền tảng olm trong lĩnh vực giáo dục. Về vấn đề tải giáo án của olm. Olm xin trả lời như sau:
Hiện nay những gì thuộc về olm mà olm cho phép tải miễn phí thì quý thầy cô có thể tải. Những gì thuộc về olm mà olm chưa cho phép hoặc không cho phép thì thầy cô sẽ không tìm thấy để tải.
Ngoài ra những giáo án thuộc ppt thầy cô có thể đăng ký theo hướng dẫn của olm trong tài khoản của quý thầy cô ạ
Trân trọng!

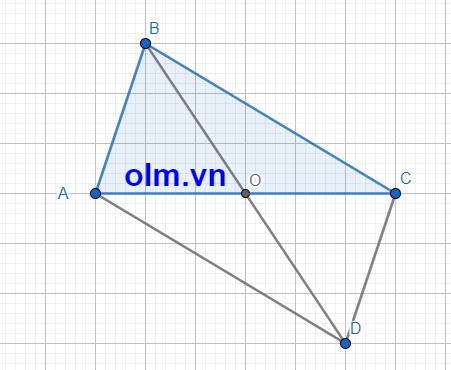
a, Xét tứ giác ABCD có: OA = OC
OB = OD
⇒ ABCD là hình bình hành ( vì tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành)
b, Chưa rõ đề yêu cầu chứng minh gì em nhá!

Lời giải:
$A=3-4x-x^2$
$-A=x^2+4x-3=(x^2+4x+4)-7=(x+2)^2-7$
Vì $(x+2)^2\geq 0$ với mọi $x$
$\Rightarrow -A=(x+2)^2-7\geq 0-7=-7$
$\Rightarrow A\leq 7$
Vậy $A_{\max}=7$. Giá trị này đạt tại $x+2=0\Leftrightarrow x=-2$


a) Do ABCD là hình bình hành
\(\Rightarrow AD=BC\) và \(AD\) // \(BC\)
Do \(AD\) // \(BC\) (cmt)
\(\Rightarrow\widehat{ADH}=\widehat{CBK}\) (so le trong)
Xét hai tam giác vuông: \(\Delta ADH\) và \(\Delta CBK\) có:
\(AD=BC\) (cmt)
\(\widehat{ADH}=\widehat{CBK}\) (cmt)
\(\Rightarrow\Delta ADH=\Delta CBK\) (cạnh huyền - góc nhọn)
\(\Rightarrow AH=CK\) (hai cạnh tương ứng)
Do \(AH\perp BD\) (gt)
\(CK\perp BD\) (gt)
\(\Rightarrow AH\) // \(CK\)
Xét tứ giác AHCK có:
\(AH\) // \(CK\) (cmt)
\(AH=CK\) (cmt)
\(\Rightarrow AHCK\) là hình bình hành
b) Do AHCK là hình bình hành (cmt)
\(I\) là trung điểm của HK (gt)
\(\Rightarrow I\) là trung điểm của AC
Do ABCD là hình bình hành (gt)
\(I\) là trung điểm của AC (cmt)
\(\Rightarrow I\) là trung điểm của BD
\(\Rightarrow IB=ID\)
a) Xét : \(\Delta ADHvà\Delta CBK\) có :
góc : AHD = góc : CKB ( = 90 độ )
AD=BC ( ABCD là hbh )
góc ADH = góc CBK ( 2 góc ở vị trí slt tạo bởi 2 đường thẳng song song là AD và BC )
Do đó : \(\Delta ADH\text{=}\Delta CBK\left(c.h-g.n\right)\)
\(\Rightarrow AH\text{=}CK\)
Xét t/g AHCK có : AH//CK ( cùng vuông góc với BD )
AH = CK (cmt)
Suy ra : t/g AHCK là hbh.
b) Từ a) : suy ra : AHCK là hbh.
Suy ra : AC cắt HK tại trung điểm của mỗi đường.
Mà I là trung điểm của HK.
Suy ra : I cũng là trung điểm của AC.
Ta có : ABCD là hbh.
Suy ra : AC cắt BD tại trung điểm của mỗi đường .
Mà I là trung điểm của AC.
Suy ra : I cũng là trung điểm của BD.
Suy ra : IB=ID.
\(B=x\left(x+3y+1\right)-2y\left(x-1\right)-\left(y+x+1\right)x\)
\(B=\left(x^2+3xy+x\right)-\left(2xy-2y\right)-\left(xy+x^2+x\right)\)
\(B=x^2+3xy+x-2xy+2y-xy-x^2-x\)
\(B=\left(x^2-x^2\right)+\left(3xy-2xy-xy\right)+\left(x-x\right)+2y\)
\(B=0+0+0+2y\)
\(B=2y\)
cậu đừng bao h gửi những cái câu ấy vào câu hỏi của người nhác nhé. nếu còn 1 lần nữa mình nhìn thấy cậu gửi thì ngay lập tức cậu sẽ bị khoá tài khoản