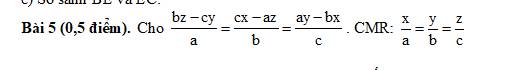cho C=3- 3mũ2+ 3mũ3- 3mũ4+....+ 3mũ23- 3mũ24. CM Cchia hết cho 420
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{bz-cy}{a}=\frac{cx-az}{b}=\frac{ay-bx}{c}$
$=\frac{abz-acy}{a^2}=\frac{bcx-abz}{b^2}=\frac{acy-bcx}{c^2}$
$=\frac{abz-acy+bcx-abz+acy-bcx}{a^2+b^2+c^2}=\frac{0}{a^2+b^2+c^2}=0$
$\Rightarrow bz-cy=cx-az=ay-bx=0$
$\Rightarrow bz=cy; cx=az; ay=bx$
$\Rightarrow \frac{y}{b}=\frac{z}{c}; \frac{z}{c}=\frac{x}{a}$
$\Rightarrow \frac{x}{a}=\frac{y}{b}=\frac{z}{c}$

vì \(x\) và y là hai đại lượng tỉ lệ thuận nên \(x\) = ky
Thay \(x\) = 3; y = -9 vào biểu thức: \(x\) = ky ta có:
3 = k.(-9) ⇒ k = 3 : (-9) = - \(\dfrac{1}{3}\)
⇒ \(x\) = - \(\dfrac{1}{3}\)y
với \(x\) = -1,5 ta có: -1,5 = - \(\dfrac{1}{3}\)y ⇒ y = -1,5.(-3) = 4,5

Lời giải:
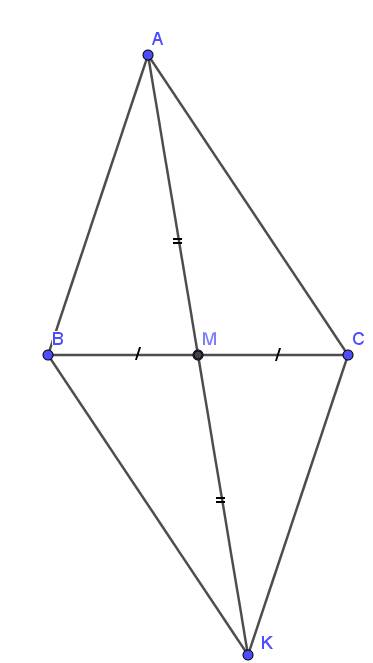
a. Xét tam giác $AMC$ và $KMB$ có:
$MC=MB$ (do $M$ là trung điểm $BC$)
$AM=KM$ (gt)
$\widehat{AMC}=\widehat{KMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle KMB$ (c.g.c)
và $\widehat{ACM}=\widehat{KBM}$
Mà 2 góc này ở vị trí so le trong nên $AC\parallel BK$
b.
Xét tam giác $ABM$ và $KCM$ có:
$BM=CM$
$AM=KM$
$\widehat{AMB}=\widehat{KMC}$ (đối đỉnh)
$\Rightarrow \triangle ABM=\triangle KCM$ (c.g.c)
$\Rightarrow \widehat{ABM}=\widehat{KCM}$
Mà 2 góc này ở vị trí so le trong nên $AB\parallel CK$

2\(^x\) - 512 = 2y
2\(^x\) - 29 = 2y
2\(^9\).(2\(^{x-9}\) - 1) = 2y
2y = 29
⇒ y = 9
2\(x-9\) - 1 = 1
2\(^{x-9}\) = 1 + 1
2\(^{x-9}\) = 2
2\(^{x-9}\) = 21
\(x-9\) = 1
\(x\) = 1 + 9
\(x\) = 10
Nếu \(x\) = 9 ⇒ 2\(^9\).(20 - 1) = 0 ≠ 2y ∀ y \(\in\) N
Nếu \(x< 9\) ⇒ 2\(^x\) < 29 < 512 ⇒ 2\(^x\) - 512 < 512 - 512 = 0 (loại)
Nếu \(x\) > 10 thì 2\(^{x-9}\) là số chẵn
⇒2\(^{x-9}\) - 1 là số lẻ ⇒ 29.(2\(^{x-9}\) - 1) ≠ 29 ∀ \(x;y\in N\)
Vậy \(x=10;y=9\)