a: \(\dfrac{24\cdot47-23}{24+47\cdot23}\cdot\dfrac{3+\dfrac{3}{7}-\dfrac{3}{11}+\dfrac{3}{101}-\dfrac{3}{13}}{\dfrac{6}{101}-\dfrac{6}{13}+\dfrac{6}{7}-\dfrac{6}{11}+6}\)

\(=\dfrac{24\cdot\left(24+23\right)-23}{24+23\left(24+23\right)}\cdot\dfrac{3\left(1+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{101}-\dfrac{1}{13}\right)}{6\left(1+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{101}-\dfrac{1}{13}\right)}\)

\(=\dfrac{24^2+24\cdot23-23}{24+23\cdot24+23^2}\cdot\dfrac{1}{2}\)

\(=\dfrac{1105}{1105}\cdot\dfrac{1}{2}=\dfrac{1}{2}\)

b: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{19\cdot21}\)

\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{19\cdot21}\right)\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{21}\right)=\dfrac{1}{2}\cdot\dfrac{20}{21}=\dfrac{10}{21}\)

Bài 2:

a: \(\left|3x+9\right|>=0\forall x;\left|5y-7\right|>=0\forall y\)

Do đó: \(\left|3x+9\right|+\left|5y-7\right|>=0\forall x,y\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}3x+9=0\\5y-7=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-3\\y=\dfrac{7}{5}\end{matrix}\right.\)

b: \(\left|x-1\dfrac{2}{3}\right|=\left|x-\dfrac{5}{3}\right|>=0\forall x\)

\(\left|4y+\dfrac{5}{6}\right|>=0\forall y\)

\(\left|3\dfrac{1}{4}-\dfrac{1}{2}z\right|>=0\forall z\)

Do đó: \(\left|x-\dfrac{5}{3}\right|+\left|4y+\dfrac{5}{6}\right|+\left|\dfrac{13}{4}-\dfrac{z}{2}\right|>=0\forall x,y,z\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{5}{3}=0\\4y+\dfrac{5}{6}=0\\\dfrac{13}{4}-\dfrac{z}{2}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}\\y=-\dfrac{5}{24}\\z=\dfrac{13}{2}\end{matrix}\right.\)

Bài 7:

\(A=\dfrac{0,375-0,3+\dfrac{3}{11}+\dfrac{3}{12}}{-0,625+0,5-\dfrac{5}{11}-\dfrac{5}{12}}+\dfrac{1,5+1-0,75}{2,5+\dfrac{5}{3}-1,25}\)

\(=\dfrac{\dfrac{3}{8}-\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}}{-\dfrac{5}{8}+\dfrac{5}{10}-\dfrac{5}{11}-\dfrac{5}{12}}+\dfrac{\dfrac{3}{2}+\dfrac{3}{3}-\dfrac{3}{4}}{\dfrac{5}{2}+\dfrac{5}{3}-\dfrac{5}{4}}\)

\(=\dfrac{3\left(\dfrac{1}{8}-\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}\right)}{-5\left(\dfrac{1}{8}-\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}\right)}+\dfrac{3\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}\right)}{5\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}\right)}\)

\(=\dfrac{3}{-5}+\dfrac{3}{5}=0\)

\(B=\dfrac{\dfrac{1}{3}-\dfrac{1}{7}-\dfrac{1}{13}}{\dfrac{2}{3}-\dfrac{2}{7}-\dfrac{2}{13}}\cdot\dfrac{\dfrac{1}{3}-0,25+0,2}{1\dfrac{1}{6}-0,875+0,7}+\dfrac{6}{7}\)

\(=\dfrac{\dfrac{1}{3}-\dfrac{1}{7}-\dfrac{1}{13}}{2\left(\dfrac{1}{3}-\dfrac{1}{7}-\dfrac{1}{13}\right)}\cdot\dfrac{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}{\dfrac{7}{6}-\dfrac{7}{8}+\dfrac{7}{10}}+\dfrac{6}{7}\)

\(=\dfrac{1}{2}\cdot\dfrac{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}{\dfrac{7}{2}\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}\right)}+\dfrac{6}{7}=\dfrac{1}{2}\cdot\dfrac{2}{7}+\dfrac{6}{7}=1\)

a) +) Để \(\dfrac{5}{x-3}\) là số hữu tỉ thì \(x-3\inℤ\) hay \(x\inℤ\)

+) Để \(\dfrac{7}{x+2}\) là số hữu tỉ thì \(x+2\inℤ\) hay \(x\inℤ\)

+) Để \(\dfrac{x+15}{x+5}\) là số hữu tỉ thì \(x+15\inℤ\) và \(x+5\inℤ\) hay \(x\inℤ\)

b) +) Để \(\dfrac{5}{x-3}\) là số dương thì \(x-3>0\) hay \(x>3\) 

+) Để \(\dfrac{7}{x+2}\) là số dương thì \(x+2>0\) hay \(x>-2\) 

+) Để \(\dfrac{x+15}{x+5}\) là số dương ta xét 2 trường hợp:

TH1:

 \(\left\{{}\begin{matrix}x+15>0\\x+5>0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x>-15\\x>-5\end{matrix}\right.\\ \Rightarrow x>-5\)

TH2:

\(\left\{{}\begin{matrix}x+15< 0\\x+5< 0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x< -15\\x< -5\end{matrix}\right.\\ \Rightarrow x< -15\)

c) +) Để \(\dfrac{5}{x-3}\) là số âm thì \(x-3< 0\) hay \(x< 3\) 

+) Để \(\dfrac{7}{x+2}\) là số âm thì \(x+2< 0\) hay \(x< -2\) 

+) Để \(\dfrac{x+15}{x+5}\) là số âm thì \(x+15>0\) và \(x+5< 0\) (vì \(x+15>x+5\))

\(\Rightarrow\left\{{}\begin{matrix}x>-15\\x< -5\end{matrix}\right.\) hay \(-15< x< -5\)

Vậy....

ai giúp mik đi mà mik vote 5sao

1 CẶP tia tạo thành 2 góc

số cặp tia khác nhau là: 29 + 28 + 27 + ....+1 = 435

số góc là: 435 x 2 =870 góc

\(\dfrac{25^2\cdot18^3}{3^2\cdot5^2\cdot2^2}\)

\(=\dfrac{5^4\cdot\left(3^2\cdot2\right)^3}{3^2\cdot5^2\cdot2^2}=\dfrac{5^4\cdot3^6\cdot2^3}{5^2\cdot3^2\cdot2^2}\)

\(=5^2\cdot3^4\cdot2=25\cdot81\cdot2=4050\)

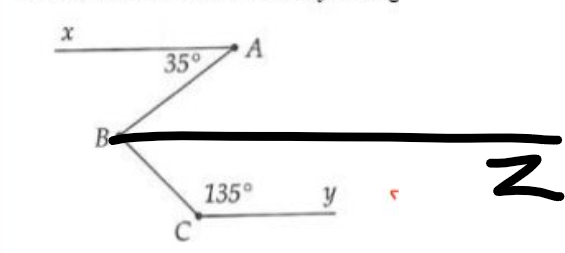
Kẻ Bz//Ax//Cy(Bz và Cy nằm trên cùng một mặt phẳng bờ chứa tia BC)

Bz//Ax

=>\(\widehat{zBA}=\widehat{xAB}\)(hai góc so le trong)

=>\(\widehat{zBA}=35^0\)

Ta có: Bz//Cy

=>\(\widehat{zBC}+\widehat{yCB}=180^0\)

=>\(\widehat{zBC}+135^0=180^0\)

=>\(\widehat{zBC}=45^0\)

\(\widehat{ABC}=\widehat{zBA}+\widehat{zBC}=35^0+45^0=80^0\)

Bài này là toán lớp 4

trong 1 giờ đội 1 làm được 1/15 phần công việc, đội 2 làm được 1/6 phần công việc

gọi a,b là thời gian đội 1 và 2 đã làm

a+b=9

a/15 + a/6 = 1

giải ra ta được a=5 và b=4

a) 

\(\left(x+\dfrac{2}{3}\right)^2=\dfrac{1}{16}\\ \Rightarrow\left(x+\dfrac{2}{3}\right)^2=\left(\dfrac{1}{4}\right)^2\\ \Rightarrow\left[{}\begin{matrix}x+\dfrac{2}{3}=\dfrac{1}{4}\\x+\dfrac{2}{3}=-\dfrac{1}{4}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{12}\\x=-\dfrac{11}{12}\end{matrix}\right.\)

Vậy...

b)

\(\dfrac{x}{15}+\dfrac{7}{20}=\dfrac{73}{60}\\ \Rightarrow\dfrac{x}{15}=\dfrac{73}{60}-\dfrac{7}{20}\\ \Rightarrow\dfrac{x}{15}=\dfrac{13}{15}\\ \Rightarrow x=13\)

Vậy...

a: \(\left(x+\dfrac{2}{3}\right)^2=\dfrac{1}{16}\)

=>\(\left[{}\begin{matrix}x+\dfrac{2}{3}=\dfrac{1}{4}\\x+\dfrac{2}{3}=-\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}-\dfrac{2}{3}=\dfrac{3}{12}-\dfrac{8}{12}=-\dfrac{5}{12}\\x=-\dfrac{1}{4}-\dfrac{2}{3}=-\dfrac{3}{12}-\dfrac{8}{12}=-\dfrac{11}{12}\end{matrix}\right.\)

b: \(\dfrac{x}{15}+\dfrac{7}{20}=\dfrac{73}{60}\)

=>\(\dfrac{x}{15}=\dfrac{73}{60}-\dfrac{21}{60}=\dfrac{52}{60}=\dfrac{13}{15}\)

=>x=13

\(\left(\dfrac{2}{3}\right)^{x+2}+\left(\dfrac{2}{3}\right)^{x+1}=\dfrac{20}{27}\\ \left(\dfrac{2}{3}\right)^{x+1}\cdot\left(\dfrac{2}{3}+1\right)=\dfrac{20}{27}\\ \left(\dfrac{2}{3}\right)^{x+1}\cdot\dfrac{5}{3}=\dfrac{20}{27}\\ \left(\dfrac{2}{3}\right)^{x+1}=\dfrac{20}{27}:\dfrac{5}{3}=\dfrac{4}{9}\\ \left(\dfrac{2}{3}\right)^{x+1}=\left(\dfrac{2}{3}\right)^2\\ x+1=2\\ x=2-1\\ x=1\)

a: \(12^{200}=\left(12^2\right)^{100}=144^{100}\)

\(5^{300}=\left(5^3\right)^{100}=125^{100}\)

mà 144>125

nên \(12^{200}>5^{300}\)

b: \(3^{2020}=\left(3^2\right)^{1010}=9^{1010}\)

\(2^{3030}=\left(2^3\right)^{1010}=8^{1010}\)

mà 9>8

nên \(3^{2020}>2^{3030}\)