Bài đã đăng bạn lưu ý không đăng lại nữa nhé, tránh gây loãng box toán.

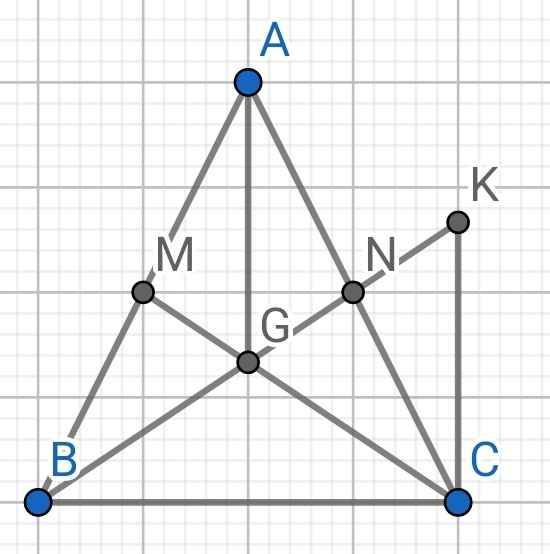
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC (1)

Do M là trung điểm của AB (gt)

⇒ AM = BM = AB : 2 (2)

Do N là trung điểm của AC (gt)

⇒ AN = CN = AC : 2 (3)

Từ (1), (2) và (3) ⇒ AM = AN

b) Xét ∆AGN và ∆CKN có:

AN = CN (cmt)

∠ANG = ∠CNK (đối đỉnh)

GN = NK (gt)

⇒ ∆AGN = ∆CKN (c-g-c)

⇒ ∠AGN = ∠CKN (hai góc tương ứng)

Mà ∠AGN và ∠CKN là hai góc so le trong

⇒ AG // CK

c) Do NG = NK (gt)

⇒ N là trung điểm của GK

⇒ GK = 2GN (4)

Do M là trung điểm của AB (gt)

N là trung điểm của AC (gt)

⇒ BN và CM là hai đường trung tuyến của ∆ABC

Mà BN cắt CM tại G (gt)

⇒ G là trọng tâm của ∆ABC

⇒ BG = 2GN (5)

Từ (4) và (5) ⇒ BG = GK

d) Do ∆AGN = ∆CKN (cmt)

⇒ AG = CK (hai cạnh tương ứng)

Do BG = 2GN (cmt)

GK = 2GN (cmt)

⇒ BG + GK = 4GN

⇒ BK = 4GN

∆BCK có:

BC + CK > BK (bất đẳng thức tam giác)

⇒ BC + CK > 4GN

Mà CK = AG (cmt)

⇒ BC + AG > 4GN

a/ 

 Ta có

\(AF\perp AC;EF\perp AD\Rightarrow\widehat{AFE}=\widehat{CAD}\) (góc có cạnh tương ứng vuông góc)

Xét tg vuông ABC có

\(AD=CD=BD=\dfrac{BC}{2}\) (Trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)

=> tg ADC cân tại D \(\Rightarrow\widehat{CAD}=\widehat{ACB}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{ACB}=\widehat{AFE}\)

Xét tg vuông ABC và tg vuông AEF

\(\widehat{A}\) chung

\(\widehat{ACB}=\widehat{AFE}\) (cmt)

=> tg ABC đồng dạng với tg AEF

b/

Xét tg vuông AEF có

\(AD^2=DE.DF\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích của hình chiếu 2 cạnh góc vuông trên cạnh huyền)

Mà \(AD=\dfrac{BC}{2}\) (cmt)

\(\Rightarrow\left(\dfrac{BC^2}{2}\right)=DE.DF\Rightarrow BC^2=4.DE.DF\)

a: ΔABC vuông tại A

mà AD là đường trung tuyến

nên DA=DB=DC

ΔDAB có DA=DB

nên ΔDAB cân tại D

Ta có: \(\widehat{DAB}+\widehat{DFA}=90^0\)(ΔDFA vuông tại D)

\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)

mà \(\widehat{DAB}=\widehat{ABC}\)(ΔDAB cân tại D)

nên \(\widehat{DFA}=\widehat{ACB}\)

Xét ΔAFE vuông tại A và ΔACB vuông tại A có

\(\widehat{AFE}=\widehat{ACB}\)

Do đó: ΔAFE~ΔACB

b: Xét ΔAEF vuông tại A có AD là đường cao

nên \(AD^2=DE\cdot DF\)

=>\(4\cdot AD^2=4\cdot DE\cdot DF\)

=>\(\left(2\cdot AD\right)^2=4\cdot DE\cdot DF\)

=>\(BC^2=4\cdot DE\cdot DF\)

Chọn B

Vì 5\(x^4\) là hạng tử có chứa bậc cao nhất của đa thức nên bậc của hạng tử này là bậc của đa thức

bậc của hạng tử này là 4

Vậy bậc của đa thức là 4

Chọn B.4

\(a+b+c=0\)

\(\Rightarrow\left(a+b+c\right)^2=a^2+b^2+c^2+2ab+2bc+2ca=0\)

\(\Leftrightarrow a^2+b^2+c^2=-2\left(ab+bc+ca\right)\)

\(A=\dfrac{a^2+b^2+c^2}{a^2+b^2-2ab+b^2+c^2-2bc+a^2+c^2-2ca}=\)

\(=\dfrac{a^2+b^2+c^2}{2\left(a^2+b^2+c^2\right)-2\left(ab+bc+ca\right)}=\)

\(=\dfrac{-2\left(ab+bc+ca\right)}{-4\left(ab+bc++ca\right)-2\left(ab+bc+ca\right)}=\dfrac{1}{3}\)

ABCD là hình thang có AB//CD

=>\(\dfrac{AB}{CD}=\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{2}{8}=\dfrac{1}{4}\)

OB/OD=1/4

=>\(S_{AOB}=\dfrac{1}{4}\times S_{AOD}=\dfrac{1}{4}\times10=2,5\left(cm^2\right)\)

\(\dfrac{OA}{OC}=\dfrac{1}{4}\)

=>OC=4OA

=>\(S_{BOC}=4\times S_{AOB}=10\left(cm^2\right)\)

\(\dfrac{OA}{OC}=\dfrac{1}{4}\)

=>\(OC=4\times OA\)

=>\(S_{DOC}=4\times S_{AOD}=40\left(cm^2\right)\)

\(S_{ABCD}=S_{AOB}+S_{BOC}+S_{DOC}+S_{AOD}\)

\(=40+10+10+2,5=62,5\left(cm^2\right)\)

b.

\(\left\{{}\begin{matrix}BD\perp AC\\CE\perp AB\end{matrix}\right.\) đồng thời H là giao điểm BD, CE

\(\Rightarrow H\) là trực tâm tam giác ABC

\(\Rightarrow AF\) là đường cao thứ 3 \(\Rightarrow\widehat{AFC}=90^0\)

\(\Rightarrow\widehat{FAC}+\widehat{FCA}=180^0-\widehat{AFC}=90^0\) (1)

ADHE nội tiếp đường tròn đường kính AH, mà M là trung điểm AH

\(\Rightarrow M\) là tâm đường tròn đường kính AH

\(\Rightarrow MA=MD\Rightarrow\Delta MAD\) cân tại M

\(\Rightarrow\widehat{FAC}=\widehat{MDA}\) (2)

D, C cùng thuộc (O) \(\Rightarrow OD=OC\Rightarrow\Delta OCD\) cân tại O

\(\Rightarrow\widehat{FCA}=\widehat{ODC}\) (3)

(1);(2);(3) \(\Rightarrow\widehat{MDA}+\widehat{ODC}=90^0\)

\(\Rightarrow\widehat{MDO}=180^0-\left(\widehat{MDA}+\widehat{ODC}\right)=90^0\)

\(\Rightarrow MD\perp OD\)

\(\Rightarrow MD\) là tiếp tuyến tại D của (O)

\(P=2\left(a+b\right)-ab-7+7=2\left(a+b\right)-ab-\left(a^2+b^2+ab\right)+7\)

\(=2\left(a+b\right)-\left(a^2+2ab+b^2\right)+7\)

\(=2\left(a+b\right)-\left(a+b\right)^2+7\)

\(=8-\left(a+b-1\right)^2\le8\)

\(P_{max}=8\) khi \(\left\{{}\begin{matrix}a+b=1\\a^2+b^2+ab=7\end{matrix}\right.\) \(\Rightarrow\left(a;b\right)=\left(-2;3\right);\left(3;-2\right)\)

Lời giải:

Số học sinh giỏi chiếm số phần tổng số học sinh cả trường là:

$1-\frac{1}{3}-\frac{2}{5}=\frac{4}{15}$

Số học sinh cả trường là:

$96: \frac{4}{15}=360$ (học sinh)

Lời giải:

Thời gian người đó đi từ Lào Cai đến Phố Lu:

17 giờ - 16 giờ 15 phút = 45 phút =0,75 giờ

Vận tốc của người đó:

$30:0,75=40$ (km/h)