Số số hạng là \(\dfrac{2n-1-1}{2}+1=\dfrac{2n-2}{2}+1=n\left(số\right)\)

Tổng của dãy số là:

\(M=\dfrac{\left(2n-1+1\right)\cdot n}{2}=\dfrac{2n\cdot n}{2}=n^2\)

=>M là số chính phương

Đây là  cấp số cộng có d=2 và số số hạng là

\(\dfrac{2n-1-1}{2}+1=n\) số hạng

\(\Rightarrow M=\dfrac{n\left(1+2n-1\right)}{2}=n^2\) là số chính phương

Diện tíhc mảnh đất là 40x40=1600(m²)

Diện tích trồng rau là 1600x(1-70%)=480(m²)

Diện tích trồng hoa là 1600-480=1120(m²)

Số tiền cần có để trồng rau là:

480x25000=12000000(đồng)

Số tiền cần có để trồng hoa là:

1120x50000=56000000(đồng)

Tổng số tiền cần có là:

12000000+56000000=68000000(đồng)

Đề chưa rõ ràng, em bổ sung đề cho đầy đủ

a: Xét ΔAHB vuông tại H có HK là đường cao

nên \(AK\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HL là đường cao

nên \(AL\cdot AC=AH^2\left(2\right)\)

Từ (1),(2) suy ra \(AK\cdot AB=AL\cdot AC\)

=>\(\dfrac{AK}{AC}=\dfrac{AL}{AB}\)

Xét ΔAKL và ΔACB có

\(\dfrac{AK}{AC}=\dfrac{AL}{AB}\)

\(\widehat{BAC}\) chung

Do đó: ΔAKL~ΔACB

=>\(\widehat{AKL}=\widehat{ACB}\)

=>\(\widehat{BKL}+\widehat{BCL}=180^0\)

=>BKLC là tứ giác nội tiếp

\(\dfrac{3}{5}\) giờ = \(36\) phút

Tỉ số phần trăm của a và b:

\(36.100\%:20=180\%\)

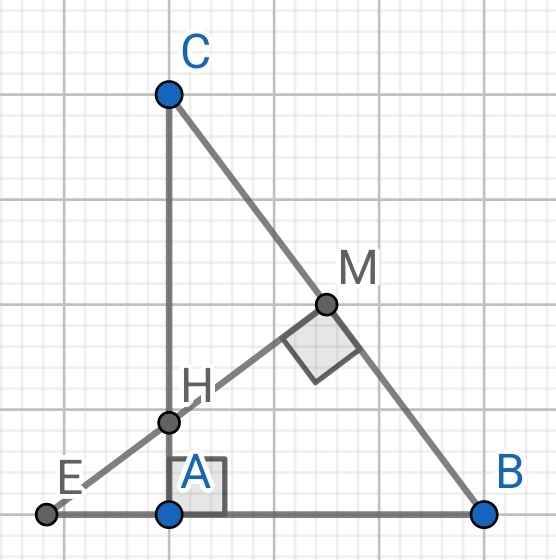
a: Xét ΔABC vuông tại A và ΔMBE vuông tại M có

\(\widehat{ABC}\) chung

Do đó: ΔABC~ΔMBE

b: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{18^2+24^2}=30\left(cm\right)\)

M là trung điểm của BC

=>\(MB=MC=\dfrac{BC}{2}=15\left(cm\right)\)

ΔBAC~ΔBME

=>\(\dfrac{BA}{BM}=\dfrac{BC}{BE}=\dfrac{AC}{ME}\)

=>\(\dfrac{18}{15}=\dfrac{30}{BE}=\dfrac{24}{ME}\)

=>\(\dfrac{30}{BE}=\dfrac{24}{ME}=\dfrac{6}{5}\)

=>BE=25(cm); ME=20(cm)

c: Xét ΔHMC vuông tại M và ΔHAE vuông tại A có

\(\widehat{MHC}=\widehat{AHE}\)(hai góc đối đỉnh)

Do đó: ΔHMC~ΔHAE

=>\(\dfrac{HM}{HA}=\dfrac{HC}{HE}\)

=>\(HM\cdot HE=HC\cdot HA\)

d: Xét ΔCEB có

CA,EM là các đường cao

CA cắt EM tại H

Do đó: H là trực tâm của ΔCEB

=>BH\(\perp\)CE tại N

Xét ΔCNB vuông tại N và ΔCME vuông tại M có

\(\widehat{NCB}\) chung

Do đó: ΔCNB~ΔCME

=>\(\dfrac{CN}{CM}=\dfrac{CB}{CE}\)

=>\(\dfrac{CN}{CB}=\dfrac{CM}{CE}\)

Xét ΔCNM và ΔCBE có

\(\dfrac{CN}{CB}=\dfrac{CM}{CE}\)

\(\widehat{NCM}\) chung

Do đó: ΔCNM~ΔCBE

=>\(\widehat{CMN}=\widehat{CEB}\)

a) Sửa đề: Chứng minh ∆ABC ∽ ∆MBE

Xét hai tam giác vuông: ∆ABC và ∆MBE có:

∠B chung

⇒ ∆ABC ∽ ∆MBE (g-g)

b) ∆ABC vuông tại A (gt)

⇒ BC² = AB² + AC² (Pythagore)

= 18² + 24²

= 900

⇒ BC = 30 (cm)

Do M là trung điểm của BC (gt)

⇒ BE = BC : 2 = 30 : 2 = 15 (cm)

Do ∆ABC ∽ ∆MBE (cmt)

⇒ AB/MB = AC/EM

⇒ 18/15 = 24/EM

⇒ EM = 15 . 24 : 18 = 20 (cm)

c) Xét hai tam giác vuông: ∆HMC và ∆HAE có:

∠MHC = ∠AHE (đối đỉnh)

⇒ ∆HMC ∽ ∆HAE (g-g)

⇒ HM/HA = HC/HE

⇒ HM.HE = HA.HC

1: Xét ΔMAC và ΔMEB có

MA=ME

\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)

MC=MB

Do đó: ΔMAC=ΔMEB

=>AC=BE

ΔMAC=ΔMEB

=>\(\widehat{MAC}=\widehat{MEB}\)

=>AC//EB

b: Xét ΔIAM và ΔKEM có

IA=KE

\(\widehat{IAM}=\widehat{KEM}\)

AM=ME

Do đó: ΔIAM=ΔKEM

=>\(\widehat{IMA}=\widehat{KME}\)

mà \(\widehat{IMA}+\widehat{IME}=180^0\)(hai góc kề bù)

nên \(\widehat{KME}+\widehat{IME}=180^0\)

=>I,M,K thẳng hàng

\(\dfrac{B}{2}=\dfrac{7}{2\cdot19\cdot31}+\dfrac{5}{2\cdot19\cdot43}+\dfrac{3}{2\cdot23\cdot43}+\dfrac{11}{2\cdot23\cdot57}\)

=>\(\dfrac{B}{2}=\dfrac{7}{31\cdot38}+\dfrac{5}{38\cdot43}+\dfrac{3}{43\cdot46}+\dfrac{11}{46\cdot57}\)

=>\(\dfrac{B}{2}=\dfrac{1}{31}-\dfrac{1}{38}+\dfrac{1}{38}-\dfrac{1}{43}+\dfrac{1}{43}-\dfrac{1}{46}+\dfrac{1}{46}-\dfrac{1}{57}\)

=>\(\dfrac{B}{2}=\dfrac{1}{31}-\dfrac{1}{57}=\dfrac{26}{1767}\)

=>\(B=\dfrac{52}{1767}\)

lỗi

tự trả lời bn ê

câu này dễ mà