A= \(\frac{\sqrt{xy}}{x-\sqrt{xy}+y}\) , so sánh \(A\) với \(\sqrt{A}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, ĐK : \(x\ge0andx+1\ge0\Leftrightarrow x\ge0andx\ge-1\Rightarrow x\ge0\)
b, ĐK : \(x-2\ge0andx-3\ge0\Leftrightarrow x\ge2andx\ge3\Rightarrow x\ge3\)
c, ĐK : \(\left(x-2\right)\left(x-3\right)\ge0\)
TH1 : \(x-2\le0andx-3\le0\Rightarrow x\le2\)
TH2 : \(x-2\ge0andx-3\ge0\Rightarrow x\ge3\)
d, ĐK : \(x^2+2x+2=x^2+2x+1+1=\left(x+1\right)^2+1>0\)
a) ĐK : \(\hept{\begin{cases}x\ge0\\x+1\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge0\\x\ge-1\end{cases}}\Leftrightarrow x\ge0\)
b) ĐK : \(\hept{\begin{cases}x-2\ge0\\x-3\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge2\\x\ge3\end{cases}}\Leftrightarrow x\ge3\)
c) ĐK : \(\left(x-2\right)\left(x-3\right)\ge0\Leftrightarrow\orbr{\begin{cases}x\ge3\\x\le2\end{cases}}\)
d) ĐK : \(x\inℝ\)


Bài 3 :
a, \(x=3-2\sqrt{2}\Rightarrow\sqrt{x}=\sqrt{3-2\sqrt{2}}=\sqrt{2}-1\)
Thay vào B ta được : \(B=\frac{7}{\sqrt{2}-1+3}=\frac{7}{\sqrt{2}+2}=\frac{7}{\sqrt{2}+2}\)
\(=\frac{7\left(\sqrt{2}-2\right)}{2-4}=-\frac{7\sqrt{2}-14}{2}\)
b, Với \(x\ge0;x\ne25\)
\(A=\frac{6\sqrt{x}}{x-25}-\frac{3}{\sqrt{x}+5}+\frac{4}{\sqrt{x}-5}\)
\(=\frac{6\sqrt{x}-3\left(\sqrt{x}-5\right)+4\left(\sqrt{x}+5\right)}{x-25}\)
\(=\frac{3\sqrt{x}+15+4\sqrt{x}+20}{x-25}=\frac{7\sqrt{x}+35}{x-25}=\frac{7}{\sqrt{x}-5}\)
Ta có : \(M=\frac{A}{B}=\frac{7}{\sqrt{x}-5}.\frac{\sqrt{x}+3}{7}=\frac{\sqrt{x}+3}{\sqrt{x}-5}\)
c, \(M< \frac{1}{2}\Rightarrow\frac{\sqrt{x}+3}{\sqrt{x}-5}-\frac{1}{2}< 0\)
\(\Leftrightarrow\frac{2\sqrt{x}+6-\sqrt{x}+5}{2\sqrt{x}-10}< 0\Leftrightarrow\frac{\sqrt{x}+11}{2\sqrt{x}-10}< 0\)
\(\Rightarrow\sqrt{x}-5< 0\Leftrightarrow x< 25\)
Kết hợp với đk vậy 0 =< x < 25

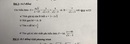



ĐK: \(xy\ge0\).
Để tồn tại \(\sqrt{A}\)thì \(A\ge0\).
Nếu \(x,y\le0\)thì \(A=\frac{\sqrt{xy}}{x+y-\sqrt{xy}}< 0\)do đó \(x,y\ge0\).
\(A=\frac{\sqrt{xy}}{x+y-\sqrt{xy}}\le\frac{\sqrt{xy}}{2\sqrt{xy}-\sqrt{xy}}=1\)
Do đó \(0\le A\le1\)nên \(\sqrt{A}\ge A\).