\(A=\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{2026^2}\)

\(=\dfrac{1}{2^2}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{1013^2}\right)\)

\(=\dfrac{1}{4}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{1013^2}\right)\)

\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)

\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)

...

\(\dfrac{1}{1013^2}< \dfrac{1}{1012\cdot1013}=\dfrac{1}{1012}-\dfrac{1}{1013}\)

Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{1013^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{1012}-\dfrac{1}{1013}\)

=>\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{1013^2}< 1-\dfrac{1}{1013}< 1\)

=>\(A=\dfrac{1}{4}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{1013^2}\right)< \dfrac{1}{4}\cdot1=\dfrac{1}{4}\)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

b: ΔAHB=ΔAHC

=>\(\widehat{HAB}=\widehat{HAC}\)

=>AH là phân giác của góc BAC

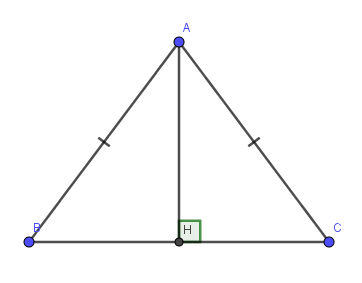
a) Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta AHC\) có:

\(AB=AC\left(gt\right)\)

\(AH\) là cạnh chung

\(\Rightarrow\Delta AHB=\Delta AHC\) (cạnh huyền - cạnh góc vuông)

b) Do \(\Delta AHB=\Delta AHC\left(cmt\right)\)

\(\Rightarrow\widehat{BAH}=\widehat{CAH}\) (hai góc tương ứng)

\(\Rightarrow AH\) là tia phân giác của \(\widehat{BAC}\)

Tỉ số giữa phần diện tích trồng hoa hồng và diện tích khu vườn là:

\(\dfrac{3}{4+3}=\dfrac{3}{7}\)

Tỉ số giữa phần diện tích trồng hoa cúc và diện tích khu vườn là:

\(\dfrac{3}{7}\cdot\dfrac{5}{6}=\dfrac{5}{14}\)

Diện tích trồng hoa đồng tiền chiếm:

\(1-\dfrac{3}{7}-\dfrac{5}{14}=\dfrac{4}{7}-\dfrac{5}{14}=\dfrac{3}{14}\)(khu vườn)

Diện tích khu vườn là:

\(90:\dfrac{3}{14}=90\cdot\dfrac{14}{3}=420\left(m^2\right)\)

Chúng ta cần tìm giá trị của biểu thức:

\(\frac{a^{2} + b^{2}}{a b}\)

khi \(a , b\) là các số nguyên dương sao cho \(a^{2} + b^{2}\) chia hết cho \(a b\), tức là biểu thức này phải là một số nguyên.

Bước 1: Viết lại biểu thức

\(\frac{a^{2} + b^{2}}{a b} = \frac{a^{2}}{a b} + \frac{b^{2}}{a b} = \frac{a}{b} + \frac{b}{a}\)

Ta đặt \(x = \frac{a}{b} + \frac{b}{a}\), trong đó \(x\) phải là một số nguyên.

Bước 2: Định nghĩa \(x\)

Ta biết rằng bất đẳng thức AM-GM cho ta:

\(\frac{a}{b} + \frac{b}{a} \geq 2\)

Do \(x\) là số nguyên dương, giá trị nhỏ nhất của \(x\) là 2.

Bước 3: Tìm các giá trị hợp lệ

Ta xét trường hợp nhỏ nhất:

\(\frac{a}{b} + \frac{b}{a} = 2\)

Điều kiện này chỉ xảy ra khi \(a = b\). Thay vào biểu thức:

\(\frac{a^{2} + a^{2}}{a^{2}} = \frac{2 a^{2}}{a^{2}} = 2\)

Kết luận:

Vì bài toán yêu cầu \(\frac{a^{2} + b^{2}}{a b}\) là một số nguyên, giá trị hợp lệ duy nhất là 2.

Vậy thương của phép chia luôn bằng 2.

Tham khảo
Ta có AB<BC<AC mà điểm B nằm trên đường thẳng AC do đó B nằm giữa A và C

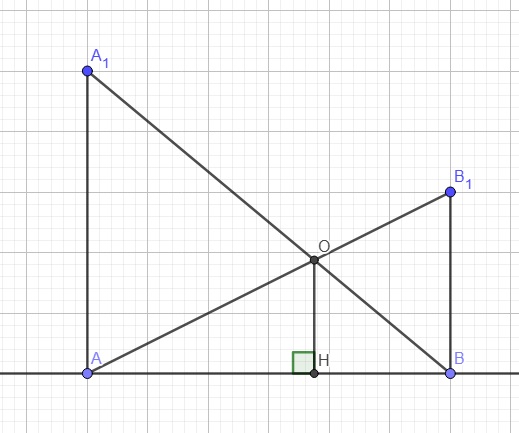
Gọi H là hình chiếu vuông góc của O lên d

\(\Rightarrow AA_1||OH||BB_1\)

Áp dụng định lý Thales trong tam giác \(ABA_1\)

\(\dfrac{OH}{AA_1}=\dfrac{BH}{AB}\)

Áp dụng định lý Thales trong tam giác \(ABB_1\)

\(\dfrac{OH}{BB1}=\dfrac{AH}{AB}\)

\(\Rightarrow\dfrac{OH}{AA_1}+\dfrac{OH}{BB_1}=\dfrac{BH}{AB}+\dfrac{AH}{AB}\)

\(\Rightarrow OH.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=1\)

\(\Rightarrow OH=\dfrac{a.b}{a+b}\)

Do a, b không đổi \(\Rightarrow OH\) không đổi

Hay khoảng cách từ O đến d không đổi khi A, B chạy trên d

Giải:

(\(x-3\))\(^5\) = 4.(\(x-3\))\(^3\)

(\(x-3\))\(^5\) - 4.(\(x-3\))\(^3\) = 0

(\(x-3\))\(^3\).[(\(x-3)^2\) - 4] = 0

\(\left[\begin{array}{l}x-3=0\\ \left(x-3\right)^2=4\end{array}\right.\)

\(\left[\begin{array}{l}x=3\\ x-3=-2\\ x-3=2\end{array}\right.\)

\(\left[\begin{array}{l}x=3\\ x=-2+3\\ x=2+3\end{array}\right.\)

\(\left[\begin{array}{l}x=3\\ x=1\\ x=5\end{array}\right.\)

Vậy \(x\in\left\lbrace1;3;5\right\rbrace\)

(x - 3)⁵ = 4(x - 3)³

(x - 3)⁵ - 4(x - 3)³ = 0

(x - 3)³.[(x - 3)² - 4] = 0

(x - 3)³.(x - 3 - 2)(x - 3 + 2) = 0

(x - 3)³(x - 5)(x - 1) = 0

(x - 3)³ = 0 hoặc x - 5 = 0 hoặc x - 1 = 0

*) (x - 3)³ = 0

x - 3 = 0

x = 3

*) x - 5 = 0

x = 5

*) x - 1 = 0

x = 1

Vậy x = 1; x = 3; x = 5