Từ ba lần kháng chiến chống quân xâm lược Mông-Nguyên, chúng ta có thể rút ra bài học về tinh thần đoàn kết, sáng tạo, kiên nhẫn và khai thác lợi thế địa phương trong việc vượt qua những thách thức hiện nay và đạt được thành công bền vững cho quốc gia của chúng ta

Thắng lợi của ba lần kháng chiến chống quân xâm lược Mông- Nguyên đã để lại nhiều bài học quý báu cho dân tộc ta

- Trước hết, đó là bài học về lòng yêu nước, tinh thần đoàn kết toàn dân khi triều đình nhà Trần thực hiện chính sách “vua tôi đồng lòng, anh em hòa thuận, cả nước góp sức” để tạo nên sức mạnh tổng hợp chống giặc

- Bài học thứ hai là chiến lược và chiến thuật quân sự linh hoạt, sáng tạo, tiêu biểu như kế sách vườn không nhà trống, lợi dụng địa hình để đánh lâu dài, chặn đánh kẻ thù trên sông Bạch Đằng

-Cuộc kháng chiến còn cho thấy vai trò của lãnh đạo sáng suốt, điển hình là Trần Quốc Tuấn với bộ “Hịch tướng sĩ”, khơi dậy tinh thần chiến đấu của quân dân

-Đặc biệt, bài học về tự cường dân tộc, không dựa vào ngoại bang mà tự đứng lên bảo vệ đất nước, vẫn còn nguyên giá trị cho đến ngày nay, nhắc nhở chúng ta phải luôn sẵn sàng trước mọi nguy cơ xâm lược và giữ vững độc lập dân tộc

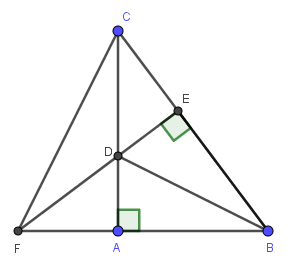
a) Do \(BD\) là tia phân giác của \(\widehat{ABC}\left(gt\right)\)

\(\Rightarrow\widehat{ABD}=\widehat{CBD}\)

\(\Rightarrow\widehat{ABD}=\widehat{EBD}\)

Xét hai tam giác vuông: \(\Delta BAD\) và \(\Delta BED\) có:

\(BD\) là cạnh chung

\(\widehat{ABD}=\widehat{EBD}\left(cmt\right)\)

\(\Rightarrow\Delta BAD=\Delta BED\) (cạnh huyền - góc nhọn)

b) Do \(\Delta BAD=\Delta BED\left(cmt\right)\)

\(\Rightarrow AD=ED\) (hai cạnh tương ứng)

Xét hai tam giác vuông: \(\Delta ADF\) và \(\Delta EDC\) có:

\(AD=ED\left(cmt\right)\)

\(\widehat{ADF}=\widehat{EDC}\) (đối đỉnh)

\(\Rightarrow\Delta ADF=\Delta EDC\) (cạnh góc vuông - góc nhọn kề)

\(AF=EC\) (hai cạnh tương ứng)

c) Do \(\Delta BAD=\Delta BED\left(cmt\right)\)

\(\Rightarrow BA=BD\) (hai cạnh tương ứng)

Lại có:

\(AF=CE\left(cmt\right)\)

\(\Rightarrow BA+AF=BE+EC\)

\(\Rightarrow BF=BC\)

\(\Rightarrow\Delta BCF\) cân tại B

a)

Xét △BAD và △BED , ta có :

góc BAD = góc BED ( cùng bằng 90°)

BD là cạnh chung

∠ABD = ∠EBD (BD là tia phân giác)

⇒ △BAD = △BED (cạnh huyền - góc nhọn)

b)

Từ △BAD = △BED ⇒ BA = BE và DA = DE

Xét △ADF và △EDC:

DA = DE

gócADF = góc EDC (đối đỉnh)

∠FAD = ∠CED = 90°

⇒ △ADF = △EDC (g. c .g)

⇒ AF = EC

c) Từ BA = BE ⇒ △BAE cân tại B

⇒ gócBAE = gócBEA

Từ △ADF = △EDC ⇒ góc AFD = góc ECD

Mà gócAFD = ∠BFC (đối đỉnh) ⇒ góc BFC = gócECD

Ta có:

gócBCF = góc BCE + gócECF

gócBFC = gócECD

Suy ra: gócBCF = gócBFC

⇒ △BCF cân tại B

.

b

Rừng Amazon, lá phổi xanh của Trái Đất, là minh chứng điển hình cho vấn đề khai thác, sử dụng và bảo vệ thiên nhiên ở Trung và Nam Mỹ

Với diện tích rộng lớn, Amazon cung cấp nguồn tài nguyên phong phú như gỗ, khoáng sản và đất nông nghiệp, nhưng đồng thời cũng đối mặt với tình trạng khai thác quá mức. Việc chặt phá rừng để lấy đất trồng trọt, chăn nuôi và khai thác gỗ đã làm giảm diện tích rừng nghiêm trọng, gây mất cân bằng sinh thái, suy giảm đa dạng sinh học và ảnh hưởng đến khí hậu toàn cầu. Bên cạnh đó, khai thác khoáng sản trái phép cũng gây ô nhiễm nguồn nước và đất

Trước thực trạng này, nhiều biện pháp bảo vệ rừng đã được thực hiện như thành lập các khu bảo tồn, tăng cường giám sát và kêu gọi sự hợp tác quốc tế nhằm hạn chế tình trạng phá rừng,.... Tuy nhiên, việc bảo vệ Amazon vẫn gặp nhiều thách thức do lợi ích kinh tế từ rừng quá lớn, đòi hỏi sự phối hợp chặt chẽ giữa chính phủ, các tổ chức môi trường và cộng đồng dân cư để hướng đến phát triển bền vững

Việc khai thác, sử dụng và bảo vệ thiên nhiên ở Trung và Nam Mỹ, đặc biệt là rừng Amazon, đang đối mặt với nhiều vấn đề quan trọng:

Khai thác tài nguyên

Sử dụng đất

Bảo vệ rừng Amazon

Kết luận, việc khai thác và sử dụng tài nguyên thiên nhiên ở Amazon cần được quản lý một cách bền vững, kết hợp giữa phát triển kinh tế và bảo vệ môi trường để bảo vệ rừng Amazon cho các thế hệ tương lai.

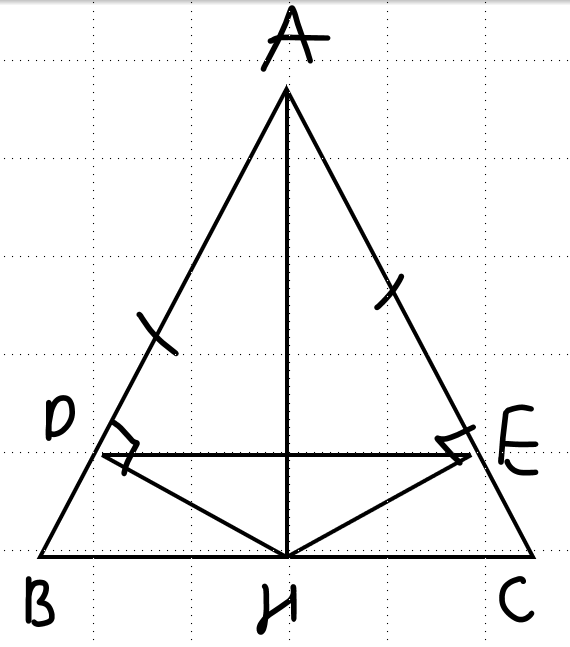
a. xét ΔABH và ΔACH, có:

AB = AC (ΔABC cân tại A)

\(\widehat{ABC}=\widehat{ACB}\left(\text{Δ}ABC\text{ cân tại A}\right)\)

HB = HC (H là trung điểm BC)

=> ΔABH = ΔACH (c-g-c)

b. trong ΔABC cân tại A có AH là đường trung tuyến

=> AH cũng là đường phân giác

\(=>\widehat{DAH}=\widehat{EAH}\) (1)

xét Δ vuông DAH và Δ vuông EAH có:

AH là cạnh chung; \(\widehat{DAH}=\widehat{EAH}\) (từ (1))

=> Δ DAH = Δ EAH (ch-gn)

=> HD = HE (2 cạnh tương ứng)

=> ΔHDE là Δ cân (tại H)

c. ta có Δ DAH = Δ EAH (câu b)

=>  AD = AE (2 cạnh tương ứng)

=> ΔDEA là Δ cân tại A

xét ΔDEA cân tại A có: \(\widehat{ADE}=\dfrac{180^0-\widehat{A}}{2}\left(2\right)\)

xét ΔABC cân tại A có: \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\left(3\right)\)

từ (2) và (3) => \(\widehat{ADE}=\widehat{ABC}\)

mà 2 góc này ở vị trí đồng vị

=> DE // BC