\(\left(2x^2+1\right)\left(3-2x\right)>0\)

mà \(2x^2+1>=1>0\forall x\)

nên -2x+3>0

=>-2x>-3

=>2x<3

=>\(x< \dfrac{3}{2}\)

a: Xét (O) có

DB,DE là các tiếp tuyến

Do đó: DB=DE

=>D nằm trên đường trung trực của BE(1)

Ta có: OB=OE

=>O nằm trên đường trung trực của BE(2)

Từ (1),(2) suy ra OD là đường trung trực của BE

=>OD\(\perp\)BE tại H

b: Xét ΔDBO vuông tại B có BH là đường cao

nên \(DH\cdot DO=DB^2\left(3\right)\)

Xét (O) có

ΔBAC nội tiếp

BC là đường kính

Do đó: ΔBAC vuông tại A

=>BA\(\perp\)DC tại A

Xét ΔDBC vuông tại B có BA là đường cao

nên \(DA\cdot DC=DB^2\left(4\right)\)

Từ (3),(4) suy ra \(DH\cdot DO=DA\cdot DC\)

=>\(\dfrac{DH}{DC}=\dfrac{DA}{DO}\)

Xét ΔDHA và ΔDCO có

\(\dfrac{DH}{DC}=\dfrac{DA}{DO}\)

góc HDA chung

Do đó: ΔDHA~ΔDCO

=>\(\widehat{DHA}=\widehat{DCO}=\widehat{ACB}\)

\(n_{Fe}=\dfrac{28}{56}=0,2\left(g\right)\\ n_{FeCl_2}=n_{Fe}=0,2\Rightarrow m=0,2.27=25,4\left(g\right)\\ V_{H_2}=0,2.2.24,79=9,916\left(l\right)\)

vvv

2 A

3 C

4 A

5 D

6 A

7 A

8 B

9 A

10 B

11 A

12 C

13 B

14 D

15 B

16 B

17 A

18 B

19 A

20 A

21 A

a: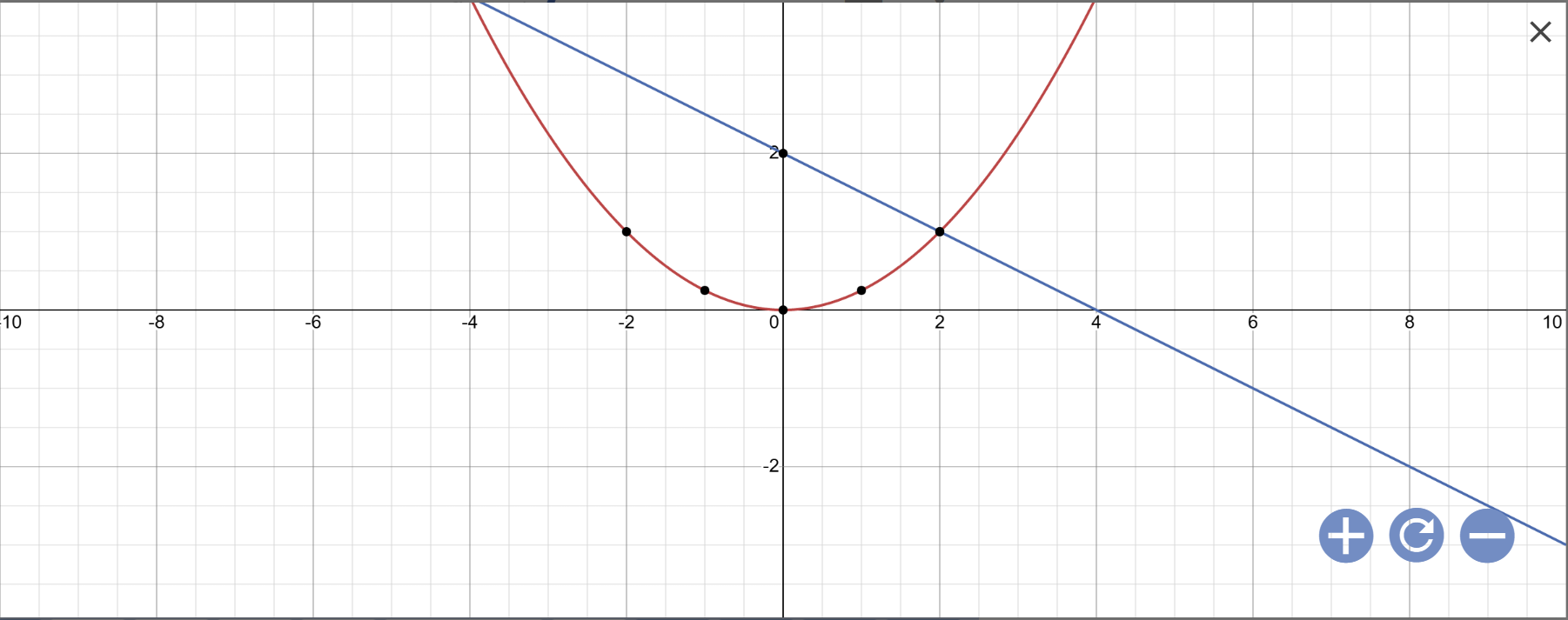 

b: Phương trình hoành độ giao điểm là:

\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x+2\)

=>\(x^2=-2x+8\)

=>\(x^2+2x-8=0\)

=>(x+4)(x-2)=0

=>\(\left[{}\begin{matrix}x+4=0\\x-2=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)

Khi x=-4 thì \(y=-\dfrac{1}{2}\cdot\left(-4\right)+2=2+2=4\)

Khi x=2 thì \(y=-\dfrac{1}{2}\cdot2+2=-1+2=1\)

Vậy: Tọa độ giao điểm của (P) và (d) là A(-4;4); B(2;1)

Vì \(\dfrac{1}{2}\ne\dfrac{2}{-3}\)

nên hệ luôn có nghiệm duy nhất

\(\left\{{}\begin{matrix}x+2y=m+3\\2x-3y=m\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x+4y=2m+6\\2x-3y=m\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x+4y-2x+3y=2m+6-m=m+6\\x+2y=m+3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}7y=m+6\\x=m+3-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{m+6}{7}\\x=m+3-2\cdot\dfrac{m+6}{7}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=\dfrac{m+6}{7}\\x=\dfrac{7m+21-2m-12}{7}=\dfrac{5m+9}{7}\end{matrix}\right.\)

x+y=-3

=>\(\dfrac{5m+9+m+6}{7}=-3\)

=>6m+15=-21

=>6m=-36

=>m=-6